KNN算法.
KNN(K-NearesNeighbor) 即K邻近法,是一个理论上比较成熟的、也是最简单的分类算法之一。KNN属于有监督学习中分类算法,虽然它看起来有点像Kmeans(Kmeans是无监督学习算法),但却是有本质的区别的.
KNN的原理就是当预测一个新的值x的时候,会根据它距离最近的K个点是什么类别来判断属于哪个类别.
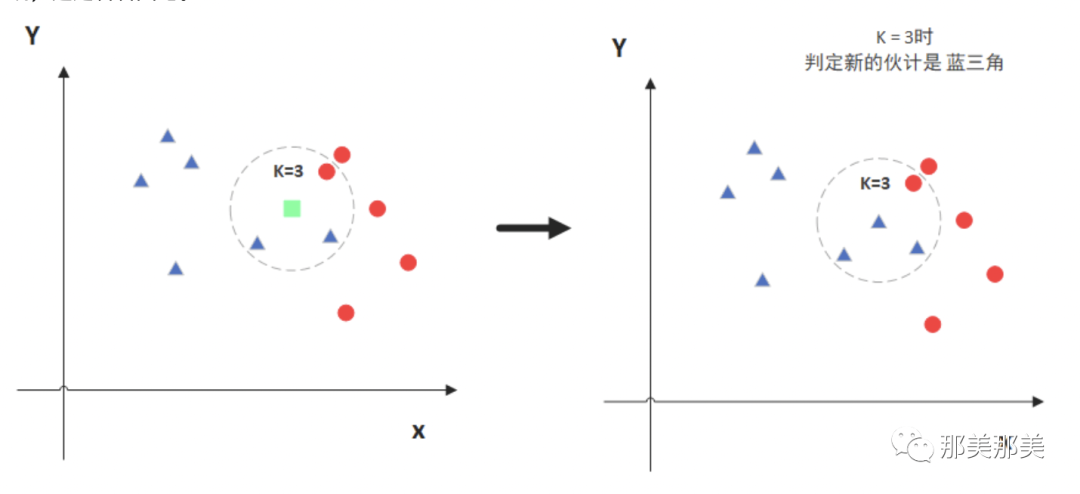
如上图虚线圆圈中, 我们要预测绿色到底是三角形还是圆形(红色那个圆点)呢?
根据KNN算法,我们假设K=3,即参考绿色附近种类最多的类型是什么(在第一个图中是三角形),那么我们就推测绿色的点可能就是三角形.
但是如果我们假设K=5,那么就不一样的,因为绿色的点要参考的就是附近5个位置的内容了,那么此时距离绿色最近的就是红色点的,那么我们推测绿色点就是红点.
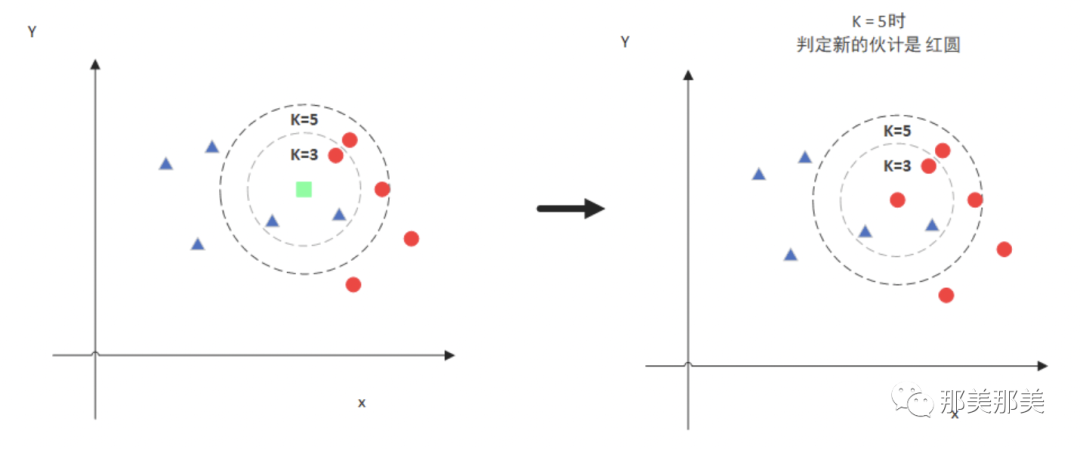
那这个绿点,到底应该是红色圆还是三角形呢? 我想你应该明白了,这个绿点,有可能会根据K设定的值而变化(好像也不准,对不对,你想对了,这个结果其实只是一个概率),所以KNN有两个东东很重要: K的取值;点距离的计算.
要计算这个距离有好几种方式,比如欧式距离、曼哈顿距离等等,不过通常说来我们会使用欧式距离.
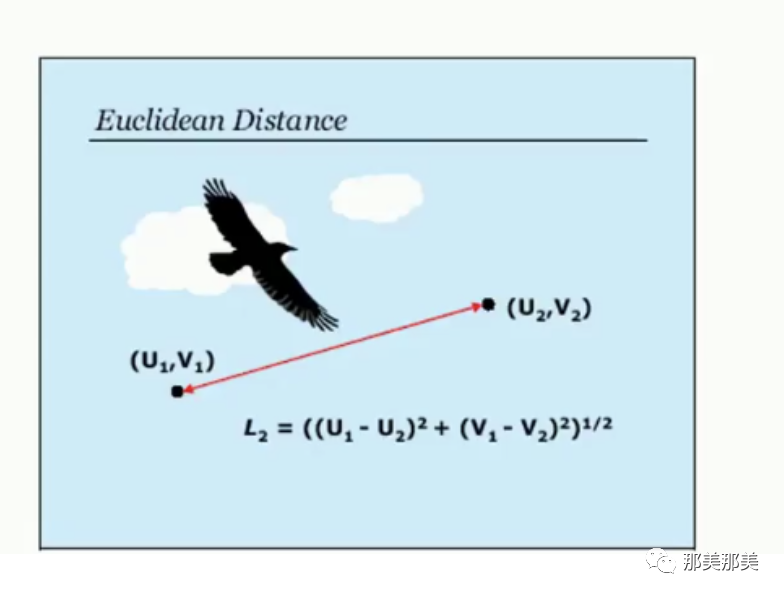
欧式距离我们这样来进行表示:
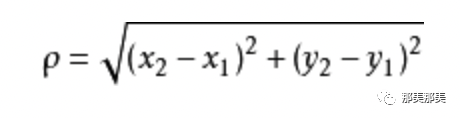
如果放到多纬空间,则公式变成:

曼哈顿距离:曼哈顿距离也叫出租车距离,用来标明两个点在标准坐标系上的绝对轴距总和.曼哈顿距离和欧氏距离的意义相近,也是为了描述两个点之间的距离,不同的是曼哈顿距离只需要做加减法,这使得计算机在大量的计算过程中代价更低,而且会消除在开平方过程中取近似值而带来的误差.

其计算公式为:
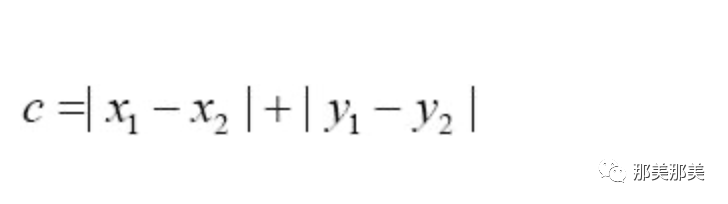
如果用多纬空间来表示,则变成:
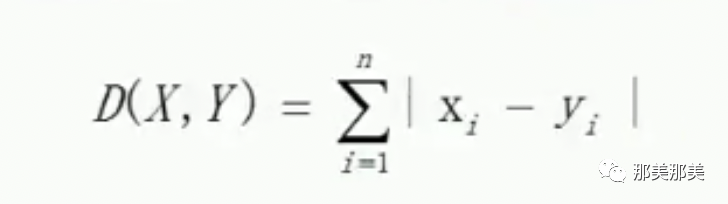
根据计算距离的公式以及我们前面说到的KNN的算,那么我们可以总结出其实现的方法为:将预测点与所有点距离进行计算,然后保存并排序,选出前面K个值看看哪些类别比较多,就是那个分类.






