来源:juejin.cn/post/7076079848824766494
通常树形结构的存储,是在子节点上存储父节点的编号来确定各节点的父子关系,例如这样的组织结构:
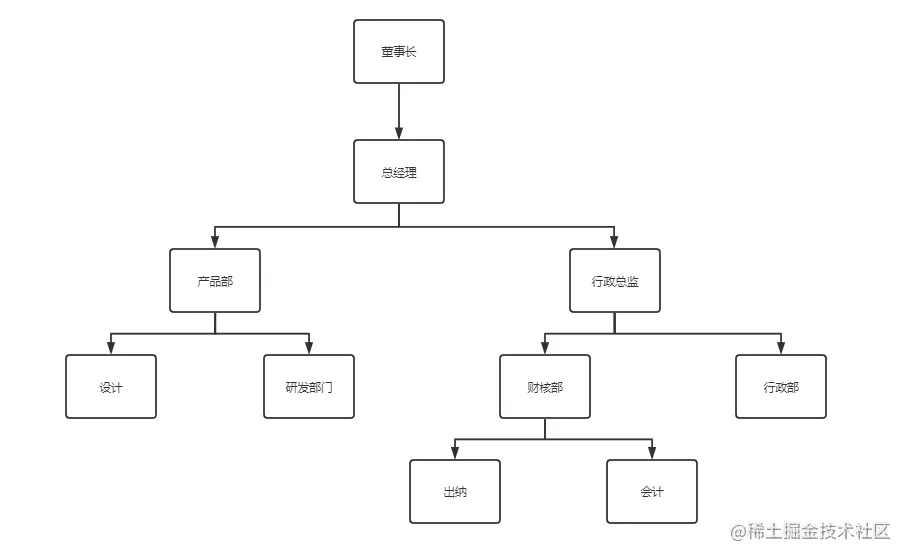
与之对应的表数据(department):
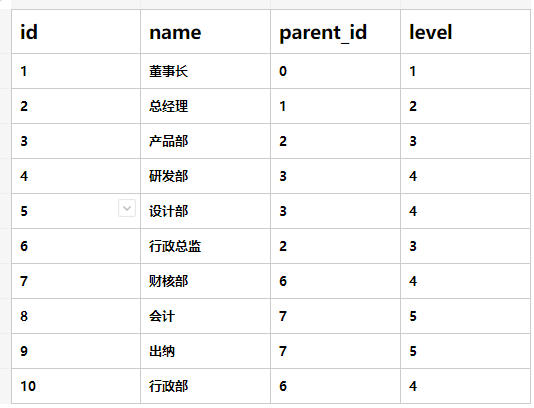
部门表结构(department)
id 部门编号name 部门名称level 所在树层级parent_id 上级部门编号
1、问题来了
这样的方式很不错,可以很直观的体现各个节点之间的关系,通常可以满足大多数需求。但是当业务需求变得多了,数据量庞大了,这样的方式就不再适合用于生产。
例如:PM加了以下需求:
查出指定部门下所有子孙部门。 查询子孙部门总数。 判断节点是否叶子节点。
查出所有子孙部门
使用指定部门编号,一层一层使用递归往下查,可能是多数人会想到的方法。尽管在mysql8.0支持了cte(公共表表达式),递归效率比传统递归方式有明显提升,但是查询效率仍会随着部门树层级深度的提高而变差。
另外一种方法,一次性查出所有数据,放入内存中处理(数据量少时,可以选用。数据量多,不怕挨打的人也可以选这种)~
查询子孙部门总数
递归查询每一层的数量,最后相加。
判断是否叶子节点
方法1:可以加字段isLeaf的方式,来表示这个节点是否是叶子节点。 方法2:直接通过查询parent_id=当前id的count是否大于0,大于0表示不是叶子节点,等于0表示为叶子节点。
在日常中,可能会经常使用上述类似方法去解决类似的问题,但我觉得这样的方法在效率上不是最优解。于是乎开始查找更好的方案去解决这些问题。
要不试试这个方法?
直到后面查到国外一博客中,见到了所谓的《改进后的先序树遍历》文章(天哪,竟然是一篇2003年发表的文章)~
https://www.sitepoint.com/hierarchical-data-database-2/
他具体是怎么做的呢?
还是回到刚刚的组织架构

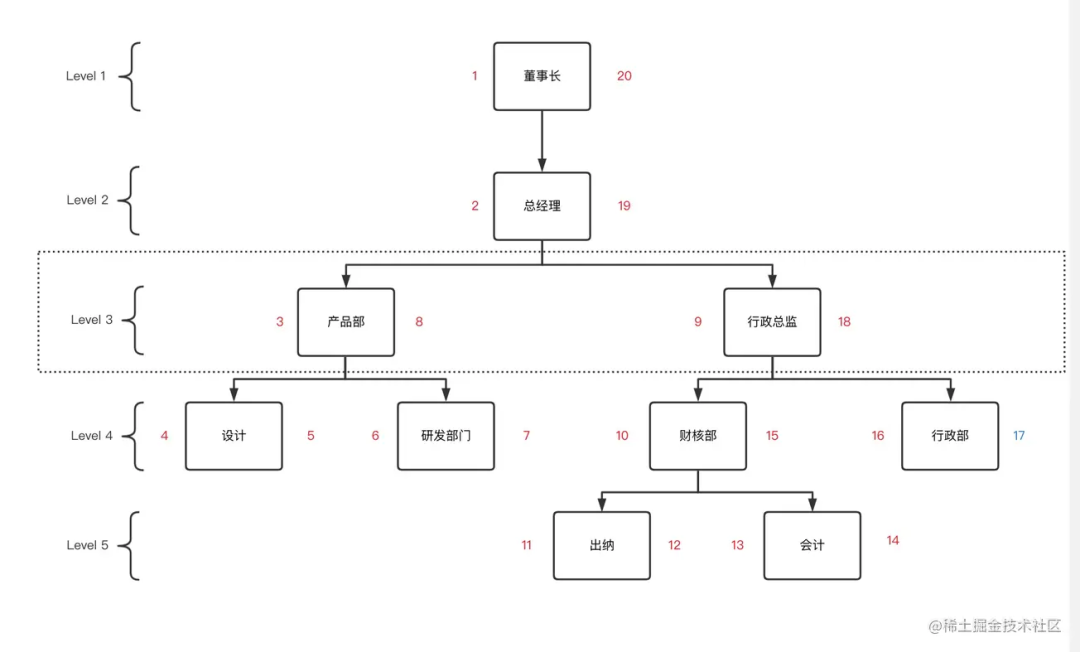
我们从根节点开始,给董事长左值设为1,下级部门总经理左值设为2,以此类推地沿着边缘开始遍历,给每个节点加上左值,遇到叶子节点处给节点加上右值,再继续向上沿着边缘继续遍历,遍历结束回到根节点右侧,你将得到类似这样的结构。
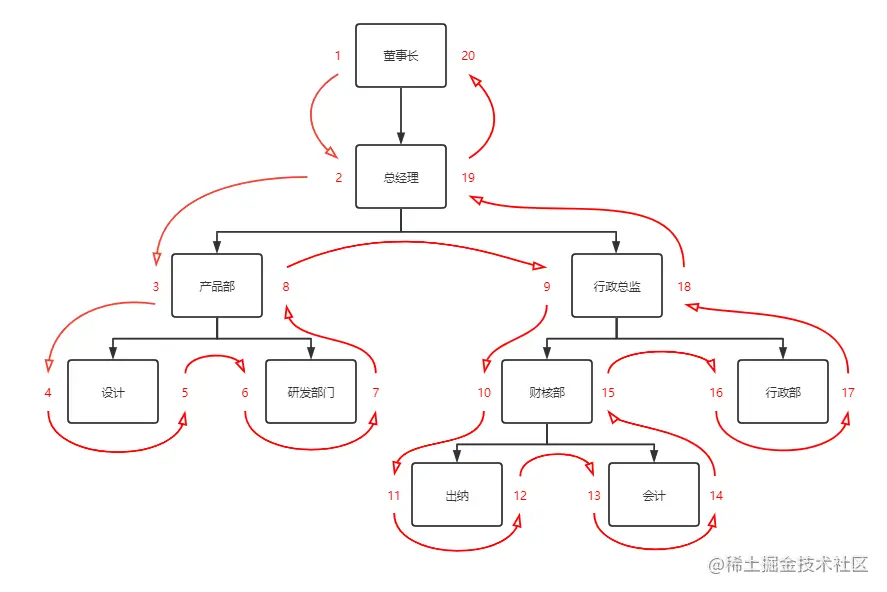
遍历完后每一个节点都有与之对应的左右值。这个时候可以去除parent_id字段,添加lft,rgt,来存储左右值。
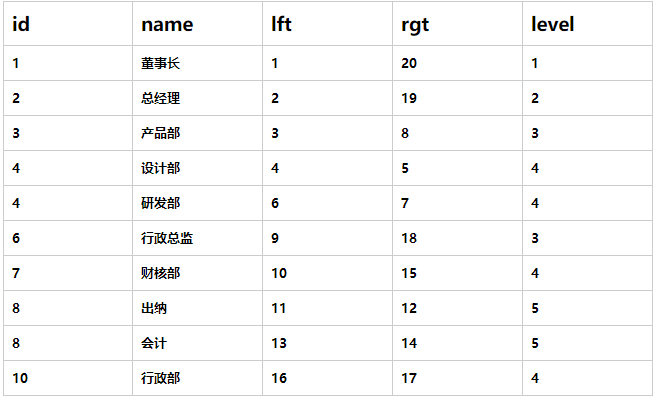
数据和结构准备完毕,我们来试试操作解决上面的需求~
查出所有子孙部门
根据当前表结构的规律,可以发现,要想查出所有子孙部门,只要查左值在 被查寻部门的左\右数之间的节点,查出来都是他的子节点。
例如:查询行政总监的所有子部门,行政总监的左右数是9和18,因此只需要用9和18做lft字段的between查询,查询出的结果就是【被查部门本身数据和所有子孙部门】;
SET @lft := 9;SET @rgt := 18;SELECT * FROM department WHERE lft BETWEEN @lft AND @rgt ORDER BY lft ASC;/*例子中用BETWEEN将被查部门本身也查了出来。实际中可以用大于小于*/
完美~
查询子孙部门总数
到这里可能会说,需求1都解决了,查总数自然也就解决了,直接上select count
就可以了,确实没有错,但是没有那个必要,因为有个简单公式可以直接计算
公式:总数 = (右值 - 左值 - 1) 2
例如:
行政总监的子孙部门数 = (18 - 9 - 1) 2 = 4董事长的子孙部门数 = (20 - 1 - 1) 2 = 9会计的子部门数 = (14 - 13 - 1) 2 = 0
可以数数看,确实没错哦~
判断是否叶子节点
通过有了上述计算公式算总数的经验后,现在判断是否叶子节点,有的小伙伴已经知道了怎么做,那就是:
右值 - 1 == 左值
那他就是叶子节点,或者左值 + 1 == 右值
那他就是叶子节点,反之则不是叶子节点。
例如:
设计部, 5 - 1 == 4
,因此他是叶子节点。董事长, 20 - 1 != 1
,因此他不是叶子节点。
至此已经完美的解决了上述需求问题,接下来再尝试一下业务的基本操作。
其他基本操作
新增部门
当新增一个部门时,需要对新增节点位置的后续边缘进行加2操作,因为每一个节点有左右两个数值。这个操作通常需要放到事务中进行处理。例如:在研发部门下添加一个新部门:
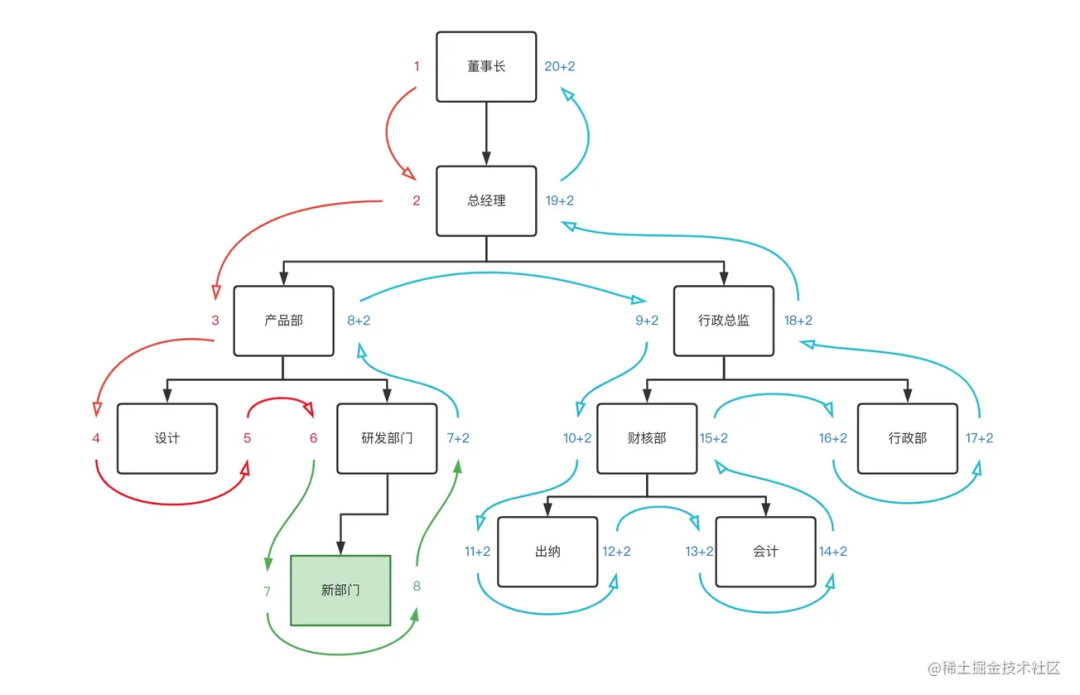
对应sql:
SET @lft := 7;/*新部门的左值*/SET @rgt := 8;/*新部门的左值*/SET @level := 5;/*新部门的层级*/begin;/*将插入的后续边缘的节点左右数+2*/UPDATE department SET lft=lft+2 WHERE lft > @lft;UPDATE department SET rgt=rgt+2 WHERE rgt >= @lft;/*插入数据*/INSERT INTO department(name,lft,rgt,level) VALUES('新部门',@lft,@rgt,level);/*新增影响行数为0时,必须回滚*/commit;/*rollback;*/
删除部门
删除部门与新增部门类似,不同的是需要对删除节点的后续边缘节点减2操作。例如:删除刚刚添加的新部门:
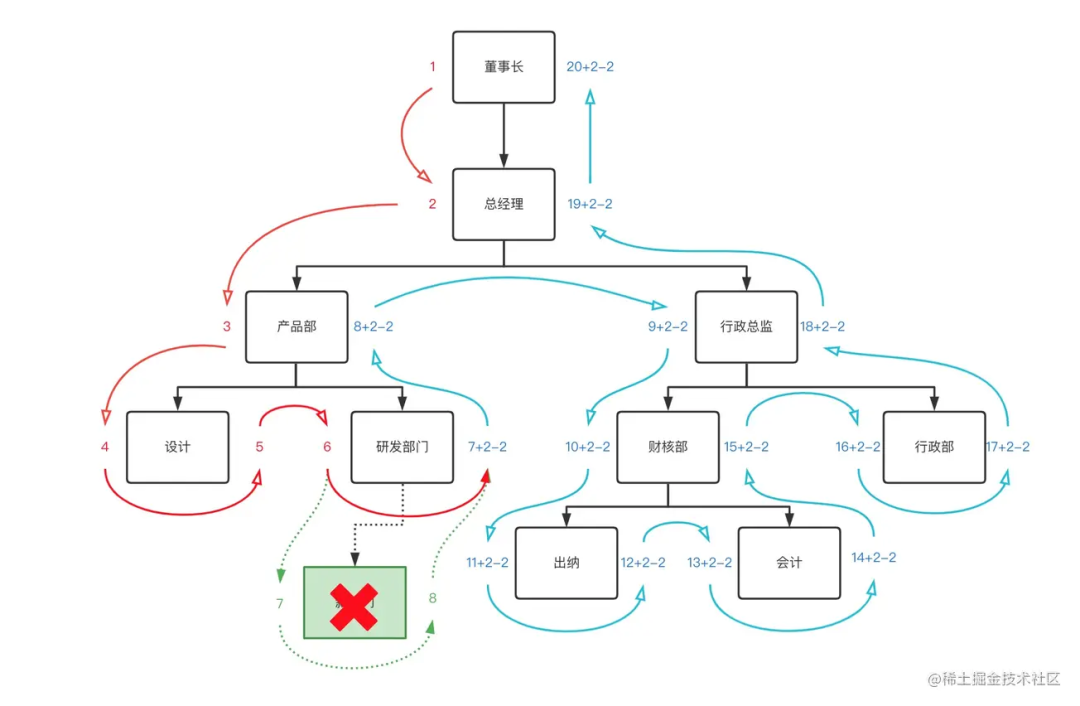
对应sql
SET @lft := 7;/*要删除的节点左值*/SET @rgt := 8;/*要删除的节点右值*/begin;UPDATE department SET lft=lft-2 WHERE lft > @lft;UPDATE department SET rgt=rgt-2 WHERE rgt > @lft;/*删除节点*/DELETE FROM department WHERE lft=@lft AND rgt=@rgt;/*删除影响行数为0时,必须回滚*/commit;/*rollback*/
查询直接子部门
查询某部门的直接子部门(即不包含孙子部门),例如:查询总经理下的直接子部门。正常需要返回产品部和行政总监
对应的sql
SET @level := 2;/*总经理的level*/SET @lft := 2;/*总经理的左值*/SET @rgt := 19;/*总经理的右值*/SELECT * FROM department WHERE lft > @lft AND rgt < @rgt AND level = @level+1;
查询祖链路径
查询某部门的祖链路径。例如:查询产品部的祖链路径,正常需要返回董事长,总经理
SET @lft := 3;/*产品部左值*/SET @rgt := 8;/*产品部右值*/SELECT * FROM department WHERE lft < @lft AND rgt > @rgt ORDER BY lft ASC;
树形数据展示(JS示例)
查出的列表数据,转成树形结构,示例:
let list = [//模拟sql查出来的列表。 {id:1,name:'root',lft:1,rgt:8,level:1}, {id:2,name:'child',lft:2,rgt:7,level:2}, {id:3,name:'grandson',lft:3,rgt:4,level:3}, {id:4,name:'grandson2',lft:5,rgt:6,level:3}];let rights = [] /*类似于一个栈结构(后进先出)*/let mp = {}//list.sort((a,b) => a.lft - b.lft)//如果你在sql中没有进行排序,需要在这里给他排序。list.forEach(item => { if(rights.length > 0) { while(rights[rights.length-1] < item.rgt) { rights.splice(-1, 1)//从rights末尾去除 } } let _level = rights.length; item._level = _level; mp[_level] = item.id item.parent_id = _level - 1 in mp ? mp[_level - 1] : null;//计算出上级部门编号 item.is_leaf = item.lft === item.rgt - 1;//判断是否叶子部门 rights.push(item.rgt)})/*上级部门计算出来了,和存parent_id的效果就一样了,后面只需要递归即可*//*递归函数 示例*/let recursive = (_list, parent_id = null) => { let _tree = []; _list.forEach(item => { if(item.parent_id == parent_id) { let childs = recursive(_list, item.id) _tree.push({ ...item, children: childs.length > 0 ? childs : (item.isLeaf ? null : []) }) } }) return _tree}console.log(recursive(list))
完结
在我目前看来,这个方法的唯一缺点就是,每一次的新增或删除,操作节点的后续边缘走到的节点都要加/减2操作。
最后给大家分享我写的SQL两件套:《SQL基础知识第二版》和《SQL高级知识第二版》的PDF电子版。里面有各个语法的解释、大量的实例讲解和批注等等,非常通俗易懂,方便大家跟着一起来实操。 有需要的读者可以下载学习,在下面的公众号「数据前线」(非本号)后台回复关键字:SQL,就行 数据前线 ——End——
后台回复关键字:1024,获取一份精心整理的技术干货
后台回复关键字:进群,带你进入高手如云的交流群。
推荐阅读









