要进行排序合并关联(Sort Merge Join),必须有一个前提:两边数据集中的数据都已经按照关联字段排序,否则,优化器会加上一个排序操作(Sort Join),使数据集按照关联字段排序。其实现的过程大致如此:从两边数据集的第一条记录开始匹配,如果数值相同,则返回记录;如果外数据记录中的数值小于内数据记录,则外数据集的游标向下移,读取下一条记录进行匹配;反正,则内数据集的游标向下移,读取下一条记录进行匹配。
IO 代价计算
从合并关联的实现过程可以看出,这种关联方式下,两边数据集都只要被扫描一次就可以完成 关联操作。因此,它的 IO 代价也就是内、外数据集的上子操作的 IO 代价。
IOCOST[SMJ] = IOCOST[Outer] + IOCOST[Inner]
提示:笛卡尔合并关联(MERGE JOIN CARTESIAN)也是以合并方式进行关联,但是内数据集的每条记录需要与外数据集做一次关联,其代价计算公式与嵌套关联相同。例如,下面第一条语句是笛卡尔合并关联操作,第二条语句是嵌套关联操作,它们的代价计算方法和结果是相同的:

CPU 代价计算
在计算排序合并关联操作的 CPU 代价时,优化器除了需要考虑内、外数据集的上子操作本身的
CPU 代价以外,还要考虑到这样一种情况:如果内、外数据集上都有多条记录的匹配字段为相同的某个数值,假设外侧有 M 条记录,内侧有 N 条记录;那么,这些数据记录之间都存在关联关系,
也就相当于要做一次笛卡尔(Cartesian)关联,即匹配数据记录数为 M*N。这样一种情况下的代价, 优化器中称之为多重匹配代价(Multiple Match Cost)。而在计算 CPU 代价时,多重匹配代价也就
成为影响代价值的重要因素之一。显然,多重匹配代价系数(multiMatchCost)的计算是和关联选 择率及关联数据集的基数相关的。其 CPU 代价计算公式为:
#CPUCYCLES[multiMatch] = GREATEST(TRUNC(CARD[Join]- GREATEST(CARD[Outer],CARD[Inner]))*100,0)
相应的,序合并关联操作的 CPU 代价估算公式为:
#CPUCYCLES[SMJ] = #CPUCYCLES[multiMatch]+#CPUCYCLES[Outer]+#CPUCYCLES[Inner]
= GREATEST(TRUNC(CARD[Join]- GREATEST(CARD[Outer],CARD[Inner])))100,0)+#CPUCYCLES[Outer]+#CPUCYCLES[Inner]
代价计算演示

先计算外据集的 IO 和 CPU 代价。索引 T_TABLES_IDX1 的索引树高度为 1,叶子数据块数为 5, 索引记录数为 2071,簇集因子为 315。表 T_TABLES 的数据记录数为 2071,字段 OWNER 的唯一值数为 21。
IOCOST[Left] = 1 + 5 + 3151
= 321
#CPUCYCLES[Left] = ROUND(321*(0.328192 + 3650 + 850)) + 2071200 + 2071130 + 2071GREATEST(1, 6, 0)*20
= 3217932
再计算内数据集的 IO 和 CPU 代价。表 T_OBJECTS 的数据块数为 830,数据记录数为 47585,字段 OWNER 的唯一值数为 22。相关的系统参数数值为:
系统统计数据收集模式:NOWORKLOAD
IOTFRSPEED:4096 IOSEEKTIM:8.381 CPUSPEEDNW:1974.735 SASIZE:208896 SMASIZE:41943040 SAMINIO:57344 OPTBLKSIZE:8192 MBRC:16
ACL[owner]:6 ACL[subobject_name]:25 ACL[created]:8
其排序的 IO 代价计算:
MREADTIM = 8.381 + 168192/4096 = 40.381 SREADTIM = 8.381 + 8192/4096 = 10.381 RROWSIZE = LEAST(123, (6+25+8)) = 39
SROWSIZE = 39 + 10 + CEIL(39/10) = 53
SDSIZE = 47585 * 53 = 2522005 MBDRC = 57344/8192 = 7
SORTWIDTH = FLOOR((41943040-((6041943040/1024/320-40*(41943040/1024/320- 1))+LOG(2,7)80)1024)/((57344+8192)2.5))
= 238
INTRUNS = GREATEST(CEIL(2522005/41943040), 2) = 2
MERGES = CEIL(LOG(238, 2)) = 1
SORTBLKS = CEIL(2522005/(8192-24)) = 309
PASSIO = CEIL(309(740.381/10.381)/(7+1)/(16-1))2 + CEIL(309(16-1-7)/(7+1)/(16-1))2
= 184
IOCOST[Sort] = 309 + 1184 = 493
IOCOST[FullTableScan] = CEIL(CEIL(830/16)(8.381+16*8192/4096)/(8.381+8192/4096)) + 1
= 204
IOCOST[Right] = IOCOST[Sort] + IOCOST[FullTableScan] = 697
内数据集的 CPU 代价计算:
BLKCYCLES = (1+1)309 * (81921.5+200*(1-57344/8192/(57344/8192+1)))
= 7609434
ROWCYCLES = ROUND((1-0.002213)15047585LOG(10,47585))
= 33312727
#CPUCYCLES[Sort] = 7609434 + 33312727 + ROUND(10.3811974.7351000)
= 61421885
#CPUCYCLES[FullTableScan] = ROUND(830(0.328192 + 3650 + 850)) + 47585130 + 47585*(1*7)*20
= 18758745
#CPUCYCLES[Right] = #CPUCYCLES[Sort] + #CPUCYCLES[FullTableScan]
= 80180630
最后计算排序合并关联操作的代价
IOCOST[SMJ] = IOCOST[Outer] + IOCOST[Inner]
= 321 + 697
= 1018
#CPUCYCLES[SMJ] = GREATEST(TRUNC(CARD[Join]-GREATEST(CARD[Outer],CARD[Inner]))*100, 0)+#CPUCYCLES[Outer]+#CPUCYCLES[Inner]
= GREATEST(TRUNC(CARD[Outer]*CARD[Inner]/GREATEST(NDV[Outer], NDV[Inner])- GREATEST(CARD[Outer],CARD[Inner]))100, 0)+#CPUCYCLES[Outer]+#CPUCYCLES[Inner]
= GREATEST(TRUNC(207147585/GREATEST(21, 22)-GREATEST(2071,47585))*100, 0)+3217932+80180630
= 526587862
计算结果和实际结果基本一致。
6.9.4 哈希关联代价计算
哈希关联(Hash Join)的实现原理是:将内外表的数据以关联字段数值的哈希值分组,仅当内外表记录的哈希值匹配时,才对关联字段进行精确匹配。
它的实现过程如下:
1、 将外表(也称为构建表)的记录依据关联字段的哈希值在内存中构建一个哈希表;
2、 扫描内表(也称为探测表)的每条记录,使用相同的哈希函数获取关联字段的哈希值, 从哈希表中找到具有相同哈希值的内表数据记录做精确匹配,将匹配的数据输出。
由于是先通过哈希值进行匹配,从而避免了内表的所有记录与外表的所有记录进行匹配比较, 从而提高关联操作的效率。这样的关联算法是经典哈希关联算法,我们称其为简单关联算法。但是, 这种关联方法中,如果外表太大,以至于内存无法容纳下整个哈希表,则只能现在内存中构建出一 个不完整的哈希表,然后扫描内表进行哈希关联,完成后,再将外表中剩余的数据构建出哈希表。 如果内存还是不足以容纳下剩余数据的哈希表,则重复这一过程(扫描内表与哈希表进行匹配), 知道全部数据完成匹配。这样就会造成多次扫描内表,从而降低性能。
因此,在经典哈希关联算法的基础上,出现了一种更高效的哈希关联算法————GRACE 哈希关联算法(因其首先出现在 GEACE 数据库系统中而得名)。这种算法的核心思想是:先将外表、内表使用一个哈希算法分区,将具有相同哈希值的数据写入一个分区。如此,内外表的每个分区是 一一匹配的。也就是说,内表中一个分区中的数据仅会与外表中的某一个分区的数据匹配。然后, 将外表中的每个分区构建一个哈希表在内存中,扫描内表中的相应分区进行哈希匹配。因为数据被 划分为多个分区,每个分区的大小远小于整个数据集的大小,因此,其哈希表被完全载入内存的概 率就更高了。而如果分区的哈希表还是大于可用内存大小,则采用另外一个哈希算法将分区化为子 分区,如此类推,直到哈希表能被完全载入内存。
在 GRACE 哈希关联算法中,每一个分区都要被先写入磁盘后,再被读入内存进行匹配。为了减少磁盘 IO,可以将外表的第 0 块分区直接构建到内存中而不写入磁盘,相应的,外表中属于第 0 个
分区的数据也不被写入磁盘,而是与内存中外表的第 0 块分区直接进行哈希关联,从而减了磁盘的读写。这一改进算法也被称为混合哈希关联算法。
混合哈希关联算法相当灵活,它可以根据当前可以工作内存大小和构建的哈希表的大小来调整分区大小。当内存足够大能容纳下整个构建的哈希表时,整个哈希表都可以放入分区 0 当中,从而
避免临时磁盘的读写;而如果内存不足时,分区 0 中的数据也同样可以避免被二次读写。因此,优化器进行哈希关联代价估算时,会根据数据量及工作区内存大小的情况,采用不同的计算公式来估 算代价。由于从 9i 到 11g,每个版本对内存的管理策略都有大幅度的改变,因而 Oracle 对像哈希关 联这样对内存依赖性较强的操作的实现也有相应的改进,其代价的估算方法也存在差异。在下面的 代价估算公式描述过程中,我会分别依据 10.2.0.4 和 11.2.0.1 分别注明 10gR2 和 11gR2 的计算差别。
哈希表数据计算
哈希表的大小以及哈希工作区的大小是决定哈希匹配过程中读写次数的重要因素。要计算哈希 关联操作的代价,首先要获得和计算哈希表的相关数据。
o 哈希表大小(Hash Table Size,HSIZE)
无论是构建表还是探测表,它们的哈希表的大小由谓词条件字段和选择字段的总的平均长度、 及内外数据集的基数计算得来。
HSIZE[Outer] = CARD[Outer]*(LEAST(ARL[Outer], SACL[Outer])+12)
HSIZE[Inner] = CARD[Inner]*(LEAST(ARL[Inner], SACL[Inner])+12)
其中,
• CARD[Outer]为外数据集的基数;CARD[Inner]为内数据集的基数
• SACL[Outer]为外表谓词条件字段和选择字段的总的平均长度;SACL[Inner]为内表谓词条件 字段和选择字段的总的平均长度;并且计算采用的长度不能超过表的记录平均长度
(Average Row Length,ARL)。
SACL[Outer] = ACL[OuterCol1]+…ACL[OuterColn] SACL[Inner] = ACL[InnerCol1]+…ACL[InnerColn]
o 哈希区大小(HASHAREA)和最大哈希区大小(MAXHASHAREA)
哈希区大小决定了是否需要将哈希表划分为多个分区,也就决定了是否需要额外读写临时磁盘。哈希区大小和最大哈希区大小的计算公式如下:
MAXHASHAREA = CEIL(SMMAX2/OPTBLKSIZE) HASHAREA =
CEIL(LEAST(GREATEST(SAMAXIO4/OPTBLKSIZE,SMMIN2/OPTBLKSIZE),MAXHASHAERA0.08))
其中,
• SMMAX 为工作区最大大小,自动管理模式下由参数"_smm_max_size"决定;
• SMMIN 为工作区最小大小,自动管理模式下由参数"_smm_min_size"决定;
• SAMAXIO 为工作区数据一次读写到临时磁盘的最大大小,自动管理模式下由参数
“_smm_auto_max_io_size"决定;
• OPTBLKSIZE 为优化器采用的数据块大小,由参数”_optimizer_block_size"决定。
而哈希区大小是否可以容纳下构建哈希表则决定了是否需要将哈希分区写入临时磁盘:即当
HSIZE[Outer]大于 HASHAREA*OPTBLKSIZE 时,需要划分多个分区,并读写临时磁盘。
o 哈希表的数据块数(Hash Blocks,HASHBLKS)
Oracle 在读写哈希表的数据时,同样是以数据块为单位的。这一数据块数也是影响 IO 和 CPU 代价的重要因素。构建表的哈希数据块数称为构建片段数(Build Fragments,BULDFRAGS);探测表的哈希数据块称为探测片段数(Probe Fragments,PROBEFRAG)。总的哈希数据块数则为它们之和。
BULDFRAGS = TRUNC(HSIZE[Outer]/OPTBLKSIZE+1) PROBEFRAGS = TRUNC(HSIZE[Inner]/OPTBLKSIZE+1) HASHBLKS = BULDFRAGS + PROBEFRAGS
IO 代价计算
因为需要分别读取内外数据集生成构建哈希表和探测哈希表,因此哈希关联的 IO 代价中包含内外数据集的 IO 代价。
IOCOST[HJ] = IOCOST[Outer] + IOCOST[Inner] + IOCOST[Hash]
如果哈希工作区能容纳下整个构建哈希表(即 HSIZE[Outer]<HASHAREA*OPTBLKSIZE)时,在获取探测表数据生成哈希值的过程中就可以直接产生关联结果,因此没有额外的 IO 代价,即:
IOCOST[Hash] = 0
如果哈希工作区能无法容纳下整个构建哈希表(即 HSIZE[Outer]>HASHAREA*OPTBLKSIZE)时, 则除分区 0 以外的分区都要被先写入临时磁盘,再被读入工作区进行哈希匹配。临时磁盘读写是以多数据块为单位的直接读写,产生的相应的 IO 代价按以下公式计算:
IOCOST[Hash] = CEIL(2HASHBLKS/(MBRC- 1)(MREADTIM/SREADTIM+MBRC/TRUNC(SAMAXIO/OPTBLKSIZE) - (1+MREADTIM/SREADTIM/TRUNC(SAMAXIO/OPTBLKSIZE))))
其中,MBRC 为多数据块读的数据块数,MREADTIM 为多数据块读时间,SREADTIM 为单数据块读时间,它们有系统统计数据得来,计算方式和前面章节相同。
注意,在 10.2.0.4 中,我们注意到当以下条件成立时,优化器则采用了另外一个计算公式。当然,实际的计算可能不是做这样的简单判断来选择某个公式,而是在各种综合条件下的计算得到与 该公式相等或者相近的结果:
120/LEAST(15,MBRC) < TRUNC(SAMAXIO/OPTBLKSIZE)
IOCOST[Hash] = HASHBLKS2/(MBRC-1)((MREADTIM/SREADTIM- MBRC/LEAST(15,MBRC))+2*MBRC/15 - (LEAST(15,MBRC)+MREADTIM/SREADTIM)/15)
CPU 代价
同样因为需要分别读取内外数据集生成构建哈希表和探测哈希表,哈希关联操作的 CPU 代价中包含了读取内外数据集的 CPU 代价。此外,在进行哈希关联时,如果内外数据集的关联数值存在多条记录时,也会产生多重匹配(Multiple Match)代价。哈希关联操作的 CPU 代价中最后一个组成部分就是构建哈希表(分区)、读写临时磁盘(如果需要读写临时磁盘的话)以及探测哈希键值 的代价,计算公式为:
CPUCYCLES[HJ] = CPUCYCLES[Outer] + CPUCYCLES[Inner] + CPUCYCLES[multiMatch] + CPUCYCLES[Hash]
当关联数据集的基数大于探测数据集(内数据集)的基数时,会产生多重匹配代价:
CPUCYCLES[multiMatch] = ROUND(GREATEST(CARD[Join]-CARD[Inner],0))*100
哈希代价中则包括了读取构建数据集和探测数据集的数据以生成哈希键值的代价
(CPUCYCLES[Genkey]),以及在需要读写临时磁盘时的读写代价(CPUCYCLES[Hashio]):
CPUCYCLES[Hash] = CPUCYCLES[Genkey] + CPUCYCLES[Hashio]
其中,生成哈希键值的 CPU 代价按以下公式计算:
CPUCYCLES[Genkey] = ROUND(CPUSPEED1000SREADTIM/2+CARD[Inner]100+150GREATEST(CARD[Outer],1))
而当需要读写临时磁盘(即 HSIZE[Outer]>HASHAREAOPTBLKSIZE)时,哈希分区的读写代价则按以下公式计算:
CPUCYCLES[Hashio] = CARD[Inner]100+CEIL((OPTBLKSIZE/2+16001024/LEAST(10241024,SMAXIO))*HASHBLKS)
注意,10.2.0.4 中,我们观察到的哈希分区的读写代价计算公式稍有不同:
CPUCYCLES[Hashio] = CARD[Inner]100+CEIL((OPTBLKSIZE/2+16001024/LEAST(120*1024,SMAXIO))HASHBLKS)
代价计算演示
我们以 11.2.0.1 中的以下语句来解释代价估算过程。其中的提示用于指定关联方式及内外表。
先计算外据集的 IO 和 CPU 代价。索引 T_TABLES_IDX1 的索引树高度为 1,叶子数据块数为 5, 索引记录数为 2071,簇集因子为 315。表 T_TABLES 的数据记录数为 2071,字段 OWNER 的唯一值数为 21。
IOCOST[Left] = 1 + 5 + 3151
= 321
#CPUCYCLES[Left] = ROUND(321*(0.328192 + 3650 + 850)) + 2071200 + 2071130 + 2071GREATEST(1, 6, 0)*20
= 3217932
再计算内数据集的 IO 和 CPU 代价。表 T_OBJECTS 的数据块数为 830,数据记录数为 47585,字段 OWNER 的唯一值数为 22。相关的系统参数数值为:
系统统计数据收集模式:NOWORKLOAD
IOTFRSPEED:4096 IOSEEKTIM:8.381 CPUSPEEDNW:1974.735 SASIZE:208896 SMASIZE:41943040 SAMINIO:57344 OPTBLKSIZE:8192 MBRC:16
ACL[owner]:6 ACL[subobject_name]:25 ACL[created]:8
其排序的 IO 代价计算:
MREADTIM = 8.381 + 168192/4096 = 40.381 SREADTIM = 8.381 + 8192/4096 = 10.381 RROWSIZE = LEAST(123, (6+25+8)) = 39
SROWSIZE = 39 + 10 + CEIL(39/10) = 53
SDSIZE = 47585 * 53 = 2522005 MBDRC = 57344/8192 = 7
SORTWIDTH = FLOOR((41943040-((6041943040/1024/320-40*(41943040/1024/320- 1))+LOG(2,7)80)1024)/((57344+8192)2.5))
= 238
INTRUNS = GREATEST(CEIL(2522005/41943040), 2) = 2
MERGES = CEIL(LOG(238, 2)) = 1
SORTBLKS = CEIL(2522005/(8192-24)) = 309
PASSIO = CEIL(309(740.381/10.381)/(7+1)/(16-1))2 + CEIL(309(16-1-7)/(7+1)/(16-1))2
= 184
IOCOST[Sort] = 309 + 1184 = 493
IOCOST[FullTableScan] = CEIL(CEIL(830/16)(8.381+16*8192/4096)/(8.381+8192/4096)) + 1
= 204
IOCOST[Right] = IOCOST[Sort] + IOCOST[FullTableScan] = 697
内数据集的 CPU 代价计算:
BLKCYCLES = (1+1)309 * (81921.5+200*(1-57344/8192/(57344/8192+1)))
= 7609434
ROWCYCLES = ROUND((1-0.002213)15047585LOG(10,47585))
= 33312727
#CPUCYCLES[Sort] = 7609434 + 33312727 + ROUND(10.3811974.7351000)
= 61421885
#CPUCYCLES[FullTableScan] = ROUND(830(0.328192 + 3650 + 850)) + 47585130 + 47585*(1*7)*20
= 18758745
#CPUCYCLES[Right] = #CPUCYCLES[Sort] + #CPUCYCLES[FullTableScan]
= 80180630
最后计算排序合并关联操作的代价
IOCOST[SMJ] = IOCOST[Outer] + IOCOST[Inner]
= 321 + 697
= 1018
#CPUCYCLES[SMJ] = GREATEST(TRUNC(CARD[Join]-GREATEST(CARD[Outer],CARD[Inner]))*100, 0)+#CPUCYCLES[Outer]+#CPUCYCLES[Inner]
= GREATEST(TRUNC(CARD[Outer]*CARD[Inner]/GREATEST(NDV[Outer], NDV[Inner])- GREATEST(CARD[Outer],CARD[Inner]))100, 0)+#CPUCYCLES[Outer]+#CPUCYCLES[Inner]
= GREATEST(TRUNC(207147585/GREATEST(21, 22)-GREATEST(2071,47585))*100, 0)+3217932+80180630
= 526587862
计算结果和实际结果基本一致。
6.9.4 哈希关联代价计算
哈希关联(Hash Join)的实现原理是:将内外表的数据以关联字段数值的哈希值分组,仅当内外表记录的哈希值匹配时,才对关联字段进行精确匹配。
它的实现过程如下:
1、 将外表(也称为构建表)的记录依据关联字段的哈希值在内存中构建一个哈希表;
2、 扫描内表(也称为探测表)的每条记录,使用相同的哈希函数获取关联字段的哈希值, 从哈希表中找到具有相同哈希值的内表数据记录做精确匹配,将匹配的数据输出。
由于是先通过哈希值进行匹配,从而避免了内表的所有记录与外表的所有记录进行匹配比较, 从而提高关联操作的效率。这样的关联算法是经典哈希关联算法,我们称其为简单关联算法。但是, 这种关联方法中,如果外表太大,以至于内存无法容纳下整个哈希表,则只能现在内存中构建出一 个不完整的哈希表,然后扫描内表进行哈希关联,完成后,再将外表中剩余的数据构建出哈希表。 如果内存还是不足以容纳下剩余数据的哈希表,则重复这一过程(扫描内表与哈希表进行匹配), 知道全部数据完成匹配。这样就会造成多次扫描内表,从而降低性能。
因此,在经典哈希关联算法的基础上,出现了一种更高效的哈希关联算法————GRACE 哈希关联算法(因其首先出现在 GEACE 数据库系统中而得名)。这种算法的核心思想是:先将外表、内表使用一个哈希算法分区,将具有相同哈希值的数据写入一个分区。如此,内外表的每个分区是 一一匹配的。也就是说,内表中一个分区中的数据仅会与外表中的某一个分区的数据匹配。然后, 将外表中的每个分区构建一个哈希表在内存中,扫描内表中的相应分区进行哈希匹配。因为数据被 划分为多个分区,每个分区的大小远小于整个数据集的大小,因此,其哈希表被完全载入内存的概 率就更高了。而如果分区的哈希表还是大于可用内存大小,则采用另外一个哈希算法将分区化为子 分区,如此类推,直到哈希表能被完全载入内存。
在 GRACE 哈希关联算法中,每一个分区都要被先写入磁盘后,再被读入内存进行匹配。为了减少磁盘 IO,可以将外表的第 0 块分区直接构建到内存中而不写入磁盘,相应的,外表中属于第 0 个
分区的数据也不被写入磁盘,而是与内存中外表的第 0 块分区直接进行哈希关联,从而减了磁盘的读写。这一改进算法也被称为混合哈希关联算法。
混合哈希关联算法相当灵活,它可以根据当前可以工作内存大小和构建的哈希表的大小来调整分区大小。当内存足够大能容纳下整个构建的哈希表时,整个哈希表都可以放入分区 0 当中,从而
避免临时磁盘的读写;而如果内存不足时,分区 0 中的数据也同样可以避免被二次读写。因此,优化器进行哈希关联代价估算时,会根据数据量及工作区内存大小的情况,采用不同的计算公式来估 算代价。由于从 9i 到 11g,每个版本对内存的管理策略都有大幅度的改变,因而 Oracle 对像哈希关 联这样对内存依赖性较强的操作的实现也有相应的改进,其代价的估算方法也存在差异。在下面的 代价估算公式描述过程中,我会分别依据 10.2.0.4 和 11.2.0.1 分别注明 10gR2 和 11gR2 的计算差别。
哈希表数据计算
哈希表的大小以及哈希工作区的大小是决定哈希匹配过程中读写次数的重要因素。要计算哈希 关联操作的代价,首先要获得和计算哈希表的相关数据。
o 哈希表大小(Hash Table Size,HSIZE)
无论是构建表还是探测表,它们的哈希表的大小由谓词条件字段和选择字段的总的平均长度、 及内外数据集的基数计算得来。
HSIZE[Outer] = CARD[Outer]*(LEAST(ARL[Outer], SACL[Outer])+12)
HSIZE[Inner] = CARD[Inner]*(LEAST(ARL[Inner], SACL[Inner])+12)
其中,
• CARD[Outer]为外数据集的基数;CARD[Inner]为内数据集的基数
• SACL[Outer]为外表谓词条件字段和选择字段的总的平均长度;SACL[Inner]为内表谓词条件 字段和选择字段的总的平均长度;并且计算采用的长度不能超过表的记录平均长度
(Average Row Length,ARL)。
SACL[Outer] = ACL[OuterCol1]+…ACL[OuterColn] SACL[Inner] = ACL[InnerCol1]+…ACL[InnerColn]
o 哈希区大小(HASHAREA)和最大哈希区大小(MAXHASHAREA)
哈希区大小决定了是否需要将哈希表划分为多个分区,也就决定了是否需要额外读写临时磁盘。哈希区大小和最大哈希区大小的计算公式如下:
MAXHASHAREA = CEIL(SMMAX2/OPTBLKSIZE) HASHAREA =
CEIL(LEAST(GREATEST(SAMAXIO4/OPTBLKSIZE,SMMIN2/OPTBLKSIZE),MAXHASHAERA0.08))
其中,
• SMMAX 为工作区最大大小,自动管理模式下由参数"_smm_max_size"决定;
• SMMIN 为工作区最小大小,自动管理模式下由参数"_smm_min_size"决定;
• SAMAXIO 为工作区数据一次读写到临时磁盘的最大大小,自动管理模式下由参数
“_smm_auto_max_io_size"决定;
• OPTBLKSIZE 为优化器采用的数据块大小,由参数”_optimizer_block_size"决定。
而哈希区大小是否可以容纳下构建哈希表则决定了是否需要将哈希分区写入临时磁盘:即当
HSIZE[Outer]大于 HASHAREA*OPTBLKSIZE 时,需要划分多个分区,并读写临时磁盘。
o 哈希表的数据块数(Hash Blocks,HASHBLKS)
Oracle 在读写哈希表的数据时,同样是以数据块为单位的。这一数据块数也是影响 IO 和 CPU 代价的重要因素。构建表的哈希数据块数称为构建片段数(Build Fragments,BULDFRAGS);探测表的哈希数据块称为探测片段数(Probe Fragments,PROBEFRAG)。总的哈希数据块数则为它们之和。
BULDFRAGS = TRUNC(HSIZE[Outer]/OPTBLKSIZE+1) PROBEFRAGS = TRUNC(HSIZE[Inner]/OPTBLKSIZE+1) HASHBLKS = BULDFRAGS + PROBEFRAGS
IO 代价计算
因为需要分别读取内外数据集生成构建哈希表和探测哈希表,因此哈希关联的 IO 代价中包含内外数据集的 IO 代价。
IOCOST[HJ] = IOCOST[Outer] + IOCOST[Inner] + IOCOST[Hash]
如果哈希工作区能容纳下整个构建哈希表(即 HSIZE[Outer]<HASHAREA*OPTBLKSIZE)时,在获取探测表数据生成哈希值的过程中就可以直接产生关联结果,因此没有额外的 IO 代价,即:
IOCOST[Hash] = 0
如果哈希工作区能无法容纳下整个构建哈希表(即 HSIZE[Outer]>HASHAREA*OPTBLKSIZE)时, 则除分区 0 以外的分区都要被先写入临时磁盘,再被读入工作区进行哈希匹配。临时磁盘读写是以多数据块为单位的直接读写,产生的相应的 IO 代价按以下公式计算:
IOCOST[Hash] = CEIL(2HASHBLKS/(MBRC- 1)(MREADTIM/SREADTIM+MBRC/TRUNC(SAMAXIO/OPTBLKSIZE) - (1+MREADTIM/SREADTIM/TRUNC(SAMAXIO/OPTBLKSIZE))))
其中,MBRC 为多数据块读的数据块数,MREADTIM 为多数据块读时间,SREADTIM 为单数据块读时间,它们有系统统计数据得来,计算方式和前面章节相同。
注意,在 10.2.0.4 中,我们注意到当以下条件成立时,优化器则采用了另外一个计算公式。当然,实际的计算可能不是做这样的简单判断来选择某个公式,而是在各种综合条件下的计算得到与 该公式相等或者相近的结果:
120/LEAST(15,MBRC) < TRUNC(SAMAXIO/OPTBLKSIZE)
IOCOST[Hash] = HASHBLKS2/(MBRC-1)((MREADTIM/SREADTIM- MBRC/LEAST(15,MBRC))+2*MBRC/15 - (LEAST(15,MBRC)+MREADTIM/SREADTIM)/15)
CPU 代价
同样因为需要分别读取内外数据集生成构建哈希表和探测哈希表,哈希关联操作的 CPU 代价中包含了读取内外数据集的 CPU 代价。此外,在进行哈希关联时,如果内外数据集的关联数值存在多条记录时,也会产生多重匹配(Multiple Match)代价。哈希关联操作的 CPU 代价中最后一个组成部分就是构建哈希表(分区)、读写临时磁盘(如果需要读写临时磁盘的话)以及探测哈希键值 的代价,计算公式为:
CPUCYCLES[HJ] = CPUCYCLES[Outer] + CPUCYCLES[Inner] + CPUCYCLES[multiMatch] + CPUCYCLES[Hash]
当关联数据集的基数大于探测数据集(内数据集)的基数时,会产生多重匹配代价:
CPUCYCLES[multiMatch] = ROUND(GREATEST(CARD[Join]-CARD[Inner],0))*100
哈希代价中则包括了读取构建数据集和探测数据集的数据以生成哈希键值的代价
(CPUCYCLES[Genkey]),以及在需要读写临时磁盘时的读写代价(CPUCYCLES[Hashio]):
CPUCYCLES[Hash] = CPUCYCLES[Genkey] + CPUCYCLES[Hashio]
其中,生成哈希键值的 CPU 代价按以下公式计算:
CPUCYCLES[Genkey] = ROUND(CPUSPEED1000SREADTIM/2+CARD[Inner]100+150GREATEST(CARD[Outer],1))
而当需要读写临时磁盘(即 HSIZE[Outer]>HASHAREAOPTBLKSIZE)时,哈希分区的读写代价则按以下公式计算:
CPUCYCLES[Hashio] = CARD[Inner]100+CEIL((OPTBLKSIZE/2+16001024/LEAST(10241024,SMAXIO))*HASHBLKS)
注意,10.2.0.4 中,我们观察到的哈希分区的读写代价计算公式稍有不同:
CPUCYCLES[Hashio] = CARD[Inner]100+CEIL((OPTBLKSIZE/2+16001024/LEAST(1201024,SMAXIO))HASHBLKS)
代价计算演示
我们以 11.2.0.1 中的以下语句来解释代价估算过程。其中的提示用于指定关联方式及内外表。


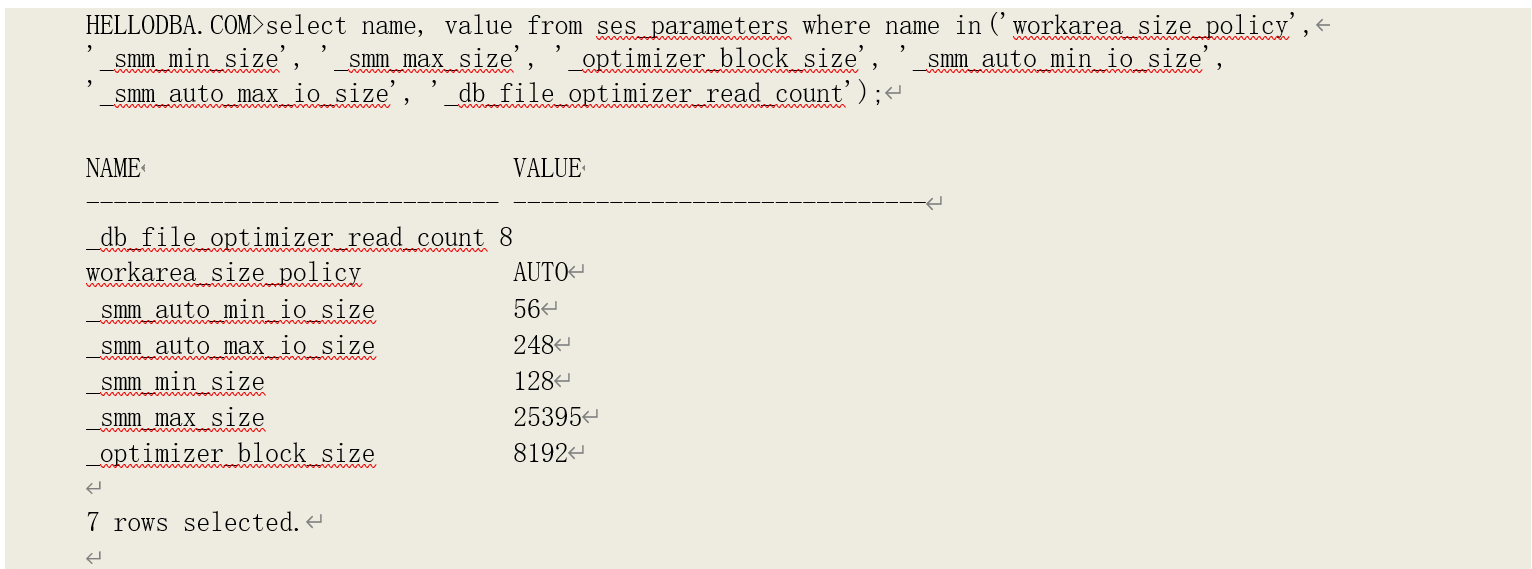
获取系统参数及系统统计数据:

然后获取表及字段的统计数据:

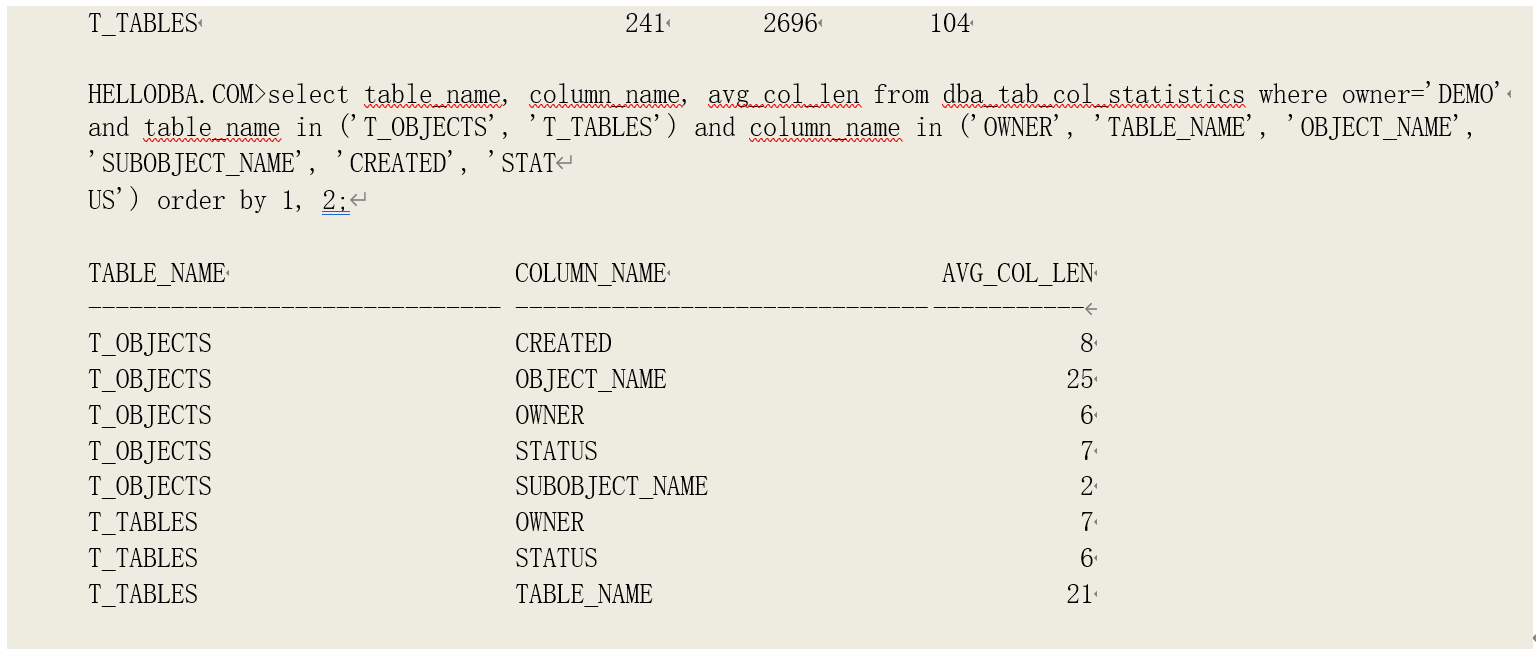
由于表 T_TABLES 的关联字段(OWNER, TABLE_NAME)上存在索引 T_TABLES_PK,我们还需要获取该索引的统计数据用于计算关联选择率:

o 系统统计数据的计算
由于当前环境的系统数据是 NOWORKLOAD 的模式先获得的,多数据块读数(MBRC)由参数
"_db_file_optimizer_read_count"的值(8)决定。相应的多数据块读时间和单数据块读时间为: SREADTIM = IOSEEKTIM + OPTBLKSIZE/IOTFRSPEED
= 10 + 8192/4096
= 12
MREADTIM = IOSEEKTIM + MBRCOPTBLKSIZE/IOTFRSPEED
= 10 + 88192/4096
= 26
o 关联选择率(JOINSEL)
由于表 T_TABLES 的关联字段(OWNER, TABLE_NAME)上存在索引 T_TABLES_PK,因此优化器采用的关联选择率由其唯一键值数计算得出:
JOINSEL = 1/NDK
= 1/2696
关联数据集的基数(CARD[Join])
CARD[Join] = CARD[Join] * CARD[Join] * JOINSEL
= 7211626961/2696
= 72116
o 哈希表大小(HSIZE)
根据对象统计数据,外表上相关字段的总平均长度(SACL[Outer])为 41,内表上相关字段的总平均长度(SACL[Inner])为 34,并且都未超过各自表的平均记录长度。相应的哈希表的大小为:
HSIZE[Outer] = CARD[Outer](LEAST(ARL[Outer], SACL[Outer])+12)
= 72116(LEAST(100, 41)+12)
= 3822148
HSIZE[Inner] = CARD[Inner](LEAST(ARL[Outer], SACL[Inner])+12)
= 2696(LEAST(241, 34)+12)
= 124016
o 哈希区大小(HASHAREA)和最大哈希区大小(MAXHASHAREA)
当前为自动关联模式,哈希区的大小由参数"_smm_max_size"、"_smm_min_size"和
"_smm_auto_max_io_size"的值决定:
MAXHASHAREA = CEIL(SMMAX2/OPTBLKSIZE)
= CEIL(2539510242/8192)
= 6349
HASHAREA = CEIL(LEAST(GREATEST(SAMAXIO4/OPTBLKSIZE,SMMIN2/OPTBLKSIZE),MAXHASHAERA0.08))
= CEIL(LEAST(GREATEST(24810244/8192,12810242/8192),6349*0.08))
= 124
哈希区的容量大小为 124*8192=1015808,小于构建哈希表的大小(3822148),因此,在计算
IO 代价和 CPU 代价时都需要考虑分区写入临时磁盘及从其读取的代价。
o 哈希表的数据块数(Hash Blocks,HASHBLKS)
有哈希表的大小不难计算出构建片段数、探测片段数以及总的哈希数据块数:
BULDFRAGS = TRUNC(HSIZE[Outer]/OPTBLKSIZE+1)
= TRUNC(3822148/8192+1)
= 467
PROBEFRAGS = TRUNC(HSIZE[Inner]/OPTBLKSIZE+1)
= TRUNC(124016/8192+1)
= 16
HASHBLKS = BULDFRAGS + PROBEFRAGS
= 467+16
= 483
o IO 代价
哈希关联的 IO 代价中包含了内外数据集的 IO 代价,我们根据内外数据集的操作(全表扫描) 的相应代价计算公式计算出他们的代价:
IOCOST[Outer] = CEIL(TABBLKS[Outer]/MBRC*MREADTIM/SREADTIM)+1
= CEIL(CEIL(830/8)26/12)+1
= 227
IOCOST[Inner] = CEIL(TABBLKS[Inner]/MBRCMREADTIM/SREADTIM)+1
= CEIL(CEIL(104/8)*26/12)+1
= 30
因为哈希区的容量大小小于构建哈希表的大小,需要计算临时磁盘读写的 IO 代价:
IOCOST[Hash] = CEIL(2HASHBLKS/(MBRC- 1)(MREADTIM/SREADTIM+MBRC/TRUNC(SAMAXIO/OPTBLKSIZE) - (1+MREADTIM/SREADTIM/TRUNC(SAMAXIO/OPTBLKSIZE))))
= CEIL(2483/(8-1)(26/12+8/TRUNC(2481024/8192) - (1+26/12/TRUNC(2481024/8192))))
= 187
哈希关联操作总的 IO 代价为:
IOCOST[HJ] = IOCOST[Outer] + IOCOST[Inner] + IOCOST[Hash]
= 227 + 30 + 187
= 444
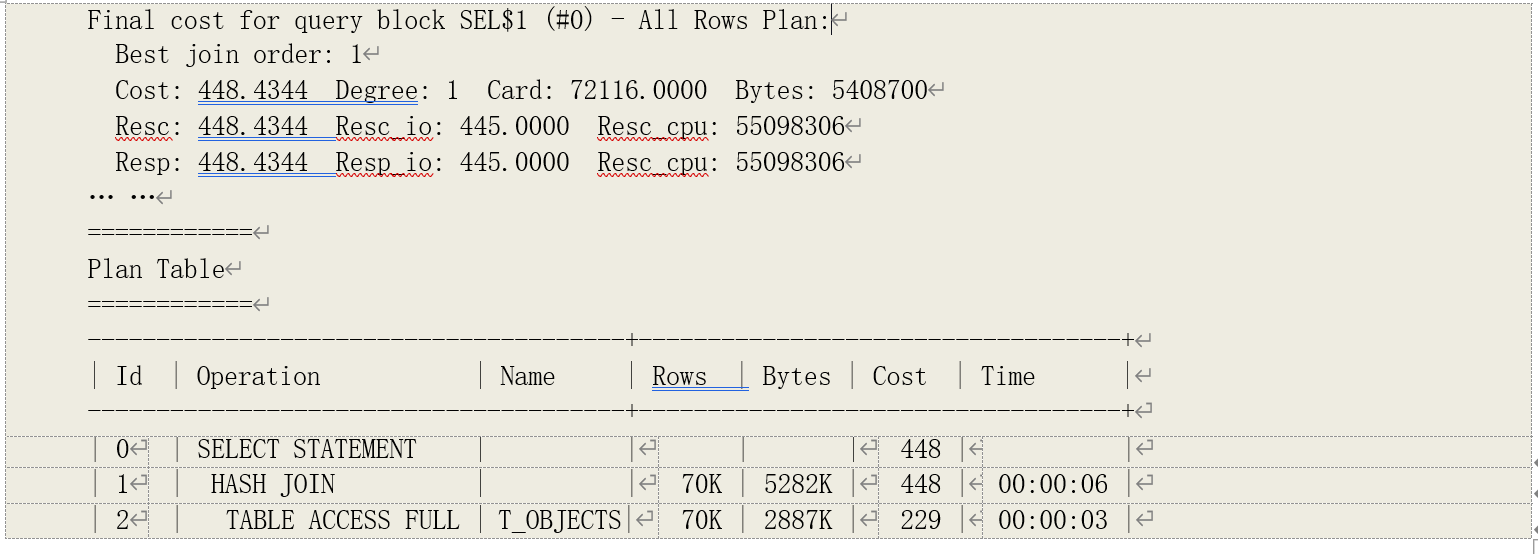
这一结果与执行计划中的实际结果基本一致,相差 1 可能是由于取整函数导致的。
o CPU 代价
同样,哈希关联的 CPU 代价中包含了内外数据集的操作的 CPU 代价:
CPUCYCLES[Outer] = ROUND(830*(0.328192 + 3650 + 850)) + 72116130 + 72116*(17)20
= 25382115
CPUCYCLES[Inner] = ROUND(104(0.328192 + 3650 + 850)) + 2696130 + 2696(1*6)*20
= 1414630
由于关联数据集的基数大于探测数据集的基数,因此会产生多重匹配代价:
CPUCYCLES[multiMatch] = ROUND(GREATEST(CARD[Join]-CARD[Inner],0))*100
= ROUND(GREATEST(72116-2696,0))*100
= 6942000
同样因为哈希区的容量大小小于构建哈希表的大小,需要计算临时磁盘读写的 CPU 代价:
CPUCYCLES[Hash] = CPUCYCLES[Genkey] + CPUCYCLES[Hashio]
= ROUND(CPUSPEED1000SREADTIM/2+CARD[Inner]100+150GREATEST(CARD[Outer],1)) + CARD[Inner]100+CEIL((OPTBLKSIZE/2+16001024/LEAST(10241024,SMAXIO))HASHBLKS)
= ROUND(1336.91275100012/2+2696100+150GREATEST(72116,1)) + 2696100+CEIL((8192/2+16001024/LEAST(10241024,2481024))*483)
= 21359562
总的 CPU 代价为:
CPUCYCLES[HJ] = CPUCYCLES[Outer] + CPUCYCLES[Inner] + CPUCYCLES[multiMatch] + CPUCYCLES[Hash]
= 25382115 + 1414630 + 6942000 + 21359562
= 55098307
与实际结果吻合。实际结果
以下为该执行计划的实际代价估算结果,与我们的计算基本吻合:
读者可以参考上例的优化器跟踪文件“06_94_10053_HJ_Demo_11gr2.trc”。






