❝「尺有所短,寸有所长;不忘初心,方得始终。」
❞
「B+tree之前以及介绍过了,不清楚的可以看看之前的文章《索引基本原理》,这里先来看看什么是跳表」。
一、什么是跳表(SkipList)
「跳表全称为跳跃列表,它允许快速查询,插入和删除一个有序连续元素的数据链表」。
跳跃列表的平均查找和插入时间复杂度都是O(logn)。
1.1 链表的结构
我们说「跳表是一个数据链表组成」的,那先来看看链表的结构:

如上图,「看起来链表与数组的结构很类似,实际上它们之间有很大的区别,可以看到上图有一个【next】,它是执行链表中下一个节点的指针,而数组是直接通过下标定位」。
所以在查找数据时:「数组可以通过下标直接快速定位,或者通过二分法查找,查找效率很快,而链表只能按照顺序通过【next】一个一个元素向后查找」。如下:

1.2 跳表的结构
了解了链表的结构,再看跳表就很好理解了,其实跳表就是在链表的基础上加了一个目录,类似书本的目录页一样,「给链表加上一个索引链表」,如下

「当我们访问某个节点时,不需要在原始链表中一个一个结点访问,而是首先访问索引链表」。例如查找节点20:
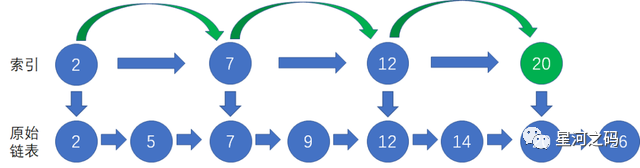
「在索引链表找到结点之后,顺着索引链表的结点向下,找到原始链表的结点」

当数据量比较大,一层索引不足以有明显的性能提升时,「可以基于原始链表的第1层索引,抽出了第2层/第3层更为稀疏的索引,结点数量是上一层索引的一半」。如下:
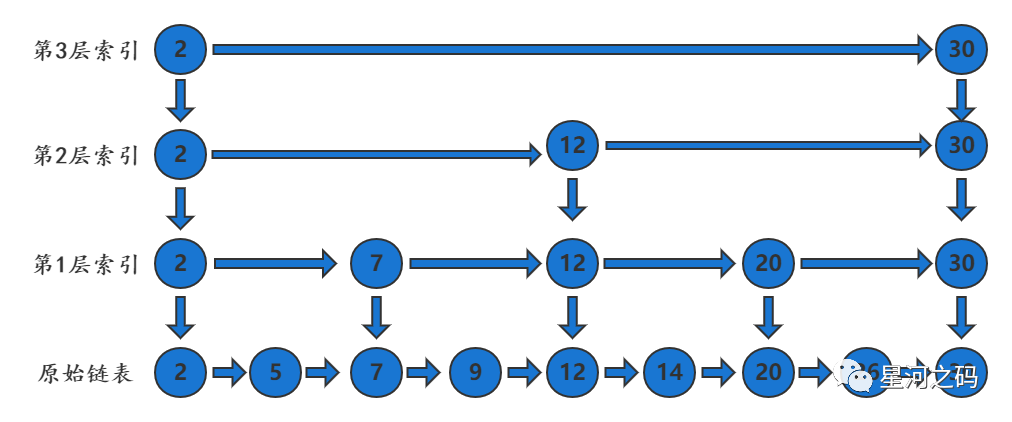
「当我们访问上述节点20时,首先从最上层索引开始查找,依次往下」:
「在第3层索引中发现20小于节点30」
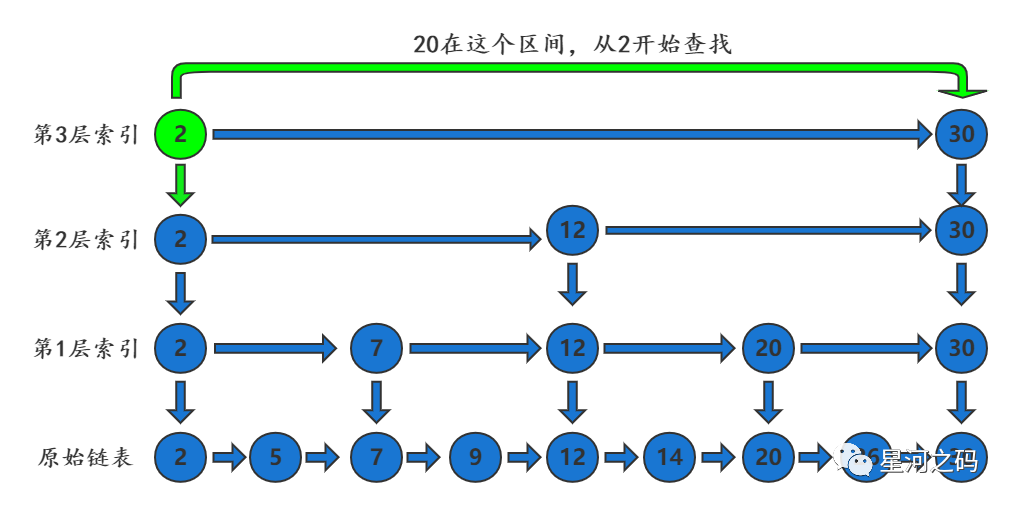
「在第2层索引中发现20大于节点2小于节点30,通过节点2向下一层索引继续查找」
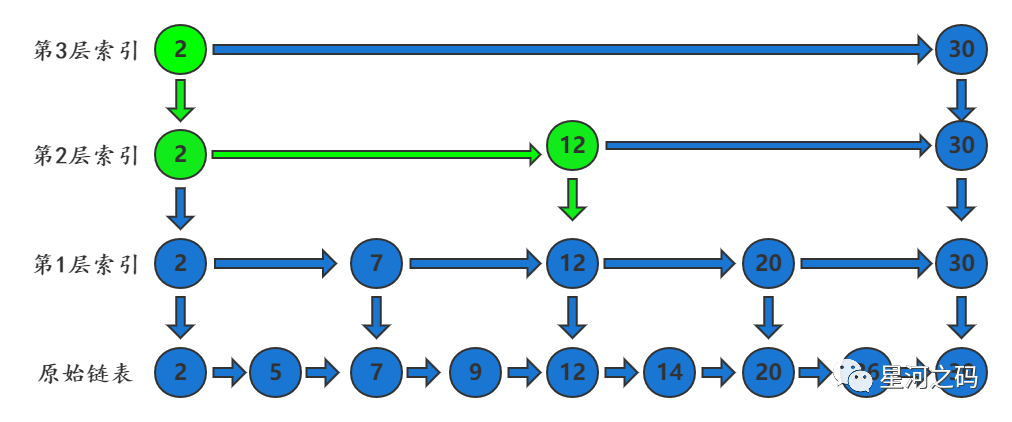
「在第1层索引中发现20大于节点12等于节点20,此时找到了节点20」
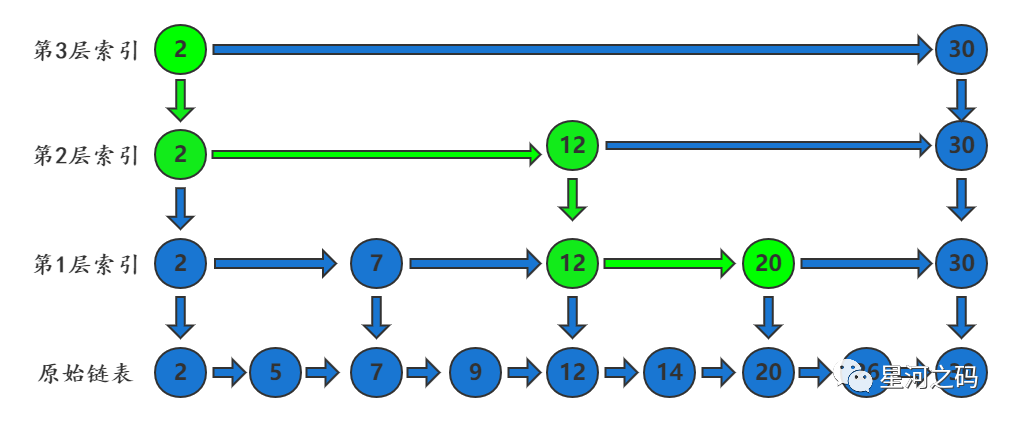
「通过第1层索引的结点20向下,找到原始链表的结点20」
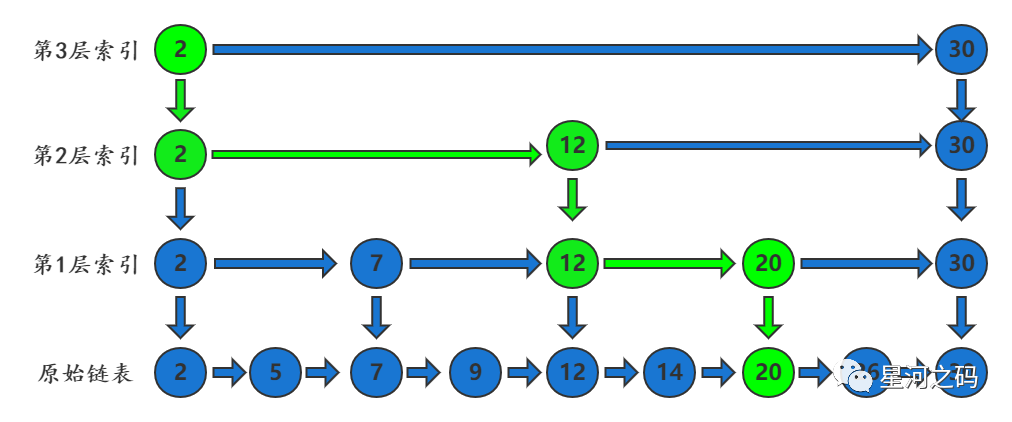
通过上述描述,可以看到通过对链表抽出索引层,可以快速定位节点位置,提升查找效率。
「当原始链表有n个结点,则索引的层级数为log(n)-1,在每一层的访问次数是常量,因此查找结点的平均时间复杂度是O(logn)」。 「相比线性依次访问链表节点的方式,性能大幅度提升,相应的由于增加了索引层,空间开销也会变大,也就是常说的空间换时间」。 「这种针对链表抽出索引层进行优化而得到的数据结构,称之为跳表」。
二、跳表的应用场景
跳表能够极大的提升效率,而且实现简单,在应用方面也比较常见
redis的zset里用到的「跳表」。 Febook开发的rocksDB的存储引擎 ElasticSearch Lucene
三 、InnoDB为什么不使用跳表
了解了跳表的基本原理之后,我们来看看InnoDB为什么不使用跳表而是使用B+tree,其实要弄清楚这个问题并不复杂,大多这类问题,无非就考虑两点:
「写入的效率」 「查询的效率」
结合这两点比较,选择一个服务应用场景的就可以了,「一般而言,大部分系统符合【二八原则】,即80%的请求是读请求,20%的请求是写请求」,所以一般考虑这个问题的时候都会侧重于查询的效率。
接下来就具体看一下跳表与B+tree的读写效率是怎么样。
3.1 跳表的写入
在上面的跳表的介绍中我们知道,「跳表的最下面一层是原始数据层,其他的都是索引,所以当我们要写入的时候,就需要在最底层的原始链表插入数据」。
例如我们现在要在上面这个链表中插入一个节点13

「第一步:在最底层的原始链表找到待插入结点的前置结点(仅小于待插入结点)」
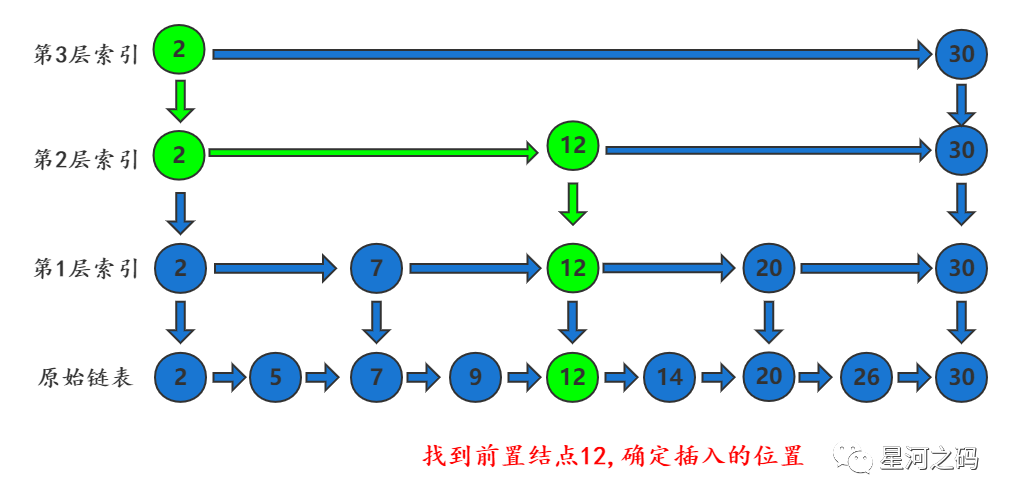
第二步:在前置结点后插入新节点
「由于最底层的原始链表就是一个普通的链表,所以按照普通链表的插入方式插入节点即可」,
❝
插入方式:新增一个节点13,将节点12指向下一个节点的指针【next的值】赋值给新节点13,更新节点12的指针【next的值】为节点13的地址
❞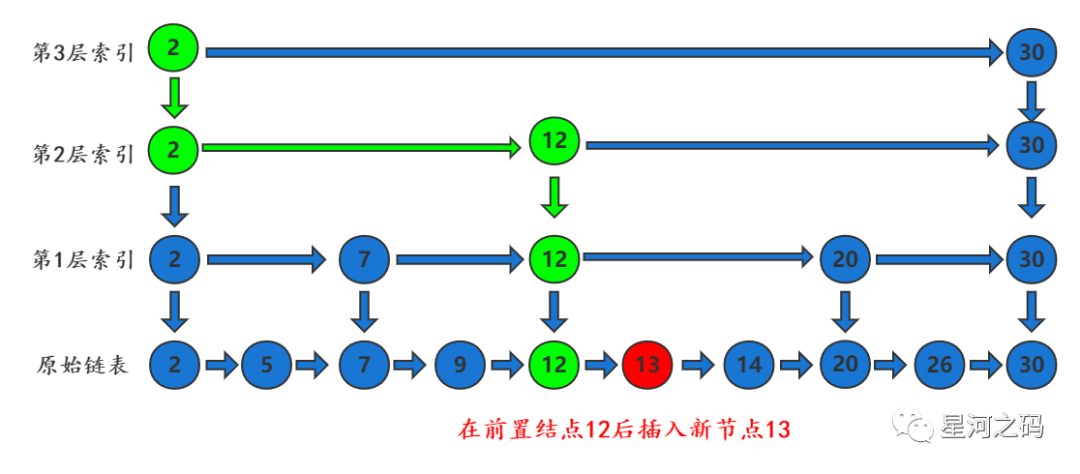
「第三步:更新索引层(这一步非必须)」
「当原始链表的节点非常多的时候,我们插入新节点后,就需要随之改变相应的索引层,并且每一层相对上一层都有50%的可能性要调整」。
理论上每一层索引的结点数都是下一层结点数的二分之一,才能满足二分的条件。
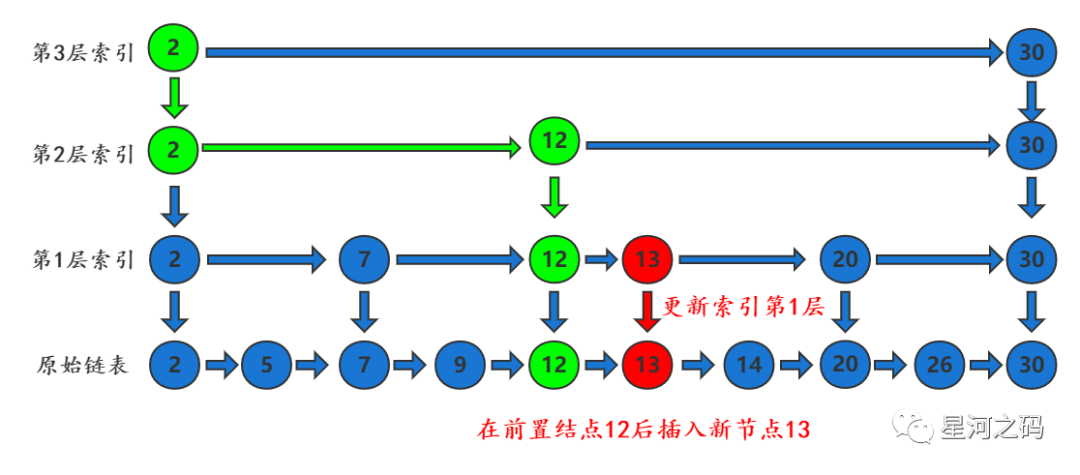
「第四步:继续更新索引层(这一步非必须)」
这一步跟第三步是一样的,基于第1层索引的链表,通过随机函数判断是否需要更新第2层索引,并且以此类推,直到索引更新完成,如果插入的节点连续随机成功,「直到超过最顶层索引,就直接加一层索引」。
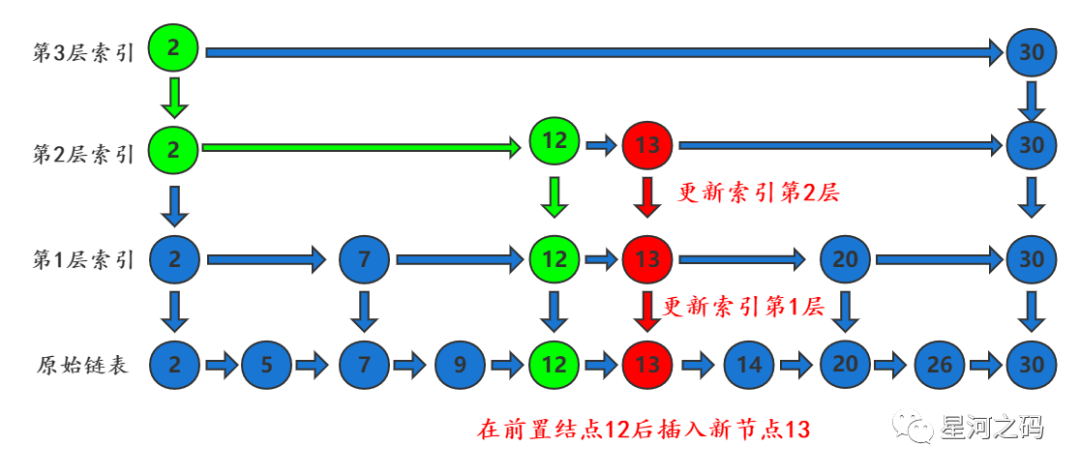
到此处,链表的插入就完成了,如果要删除节点也是一样的,先找到要删除的节点,然后依次删除原始链表,第一层索引,第二层索引 ....直到将此节点在所有索引层全部
3.2 B+Tree的写入
在索引的《索引基本原理》中介绍了B+tree的基本结构,不清楚可以看一下之前的文章,「在B+Tree由叶子结点和非叶子结点组成。跟跳表类似,最底层的叶子结点存放的是原始数据,非叶子结点存放索引,叶子结点和非叶子结点都以数据页为单位,大小为16K」
在B+Tree是一种平衡二叉树,为了保证其平衡,会使其各个分支高度都一样,当插入数据时,会更新叶子结点数据页中的数据和非叶子结点数据页中的索引,这一点跟链表很类似。
由于新增数据会更新叶子结点和非叶子结点,所以对于B+Tree会有不同的影响:
「叶子结点和非叶子结点都没满」
数据页都没满的情况下,直接找到要插入数据的叶子结点数据页,将数据写入即可。
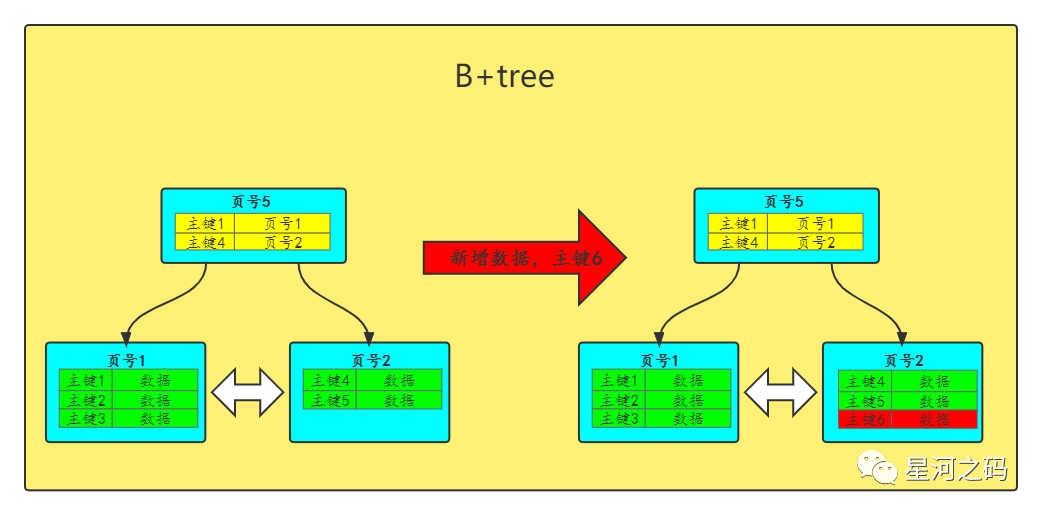
如上图,这种情况不会对B+tree的结构产生什么影响
「叶子结点满了,但非叶子结点没满」
「此时会分裂叶子结点,将包括待插入数据在内的数据均分成两个新结点,同时索引结点会增加新的索引信息」。
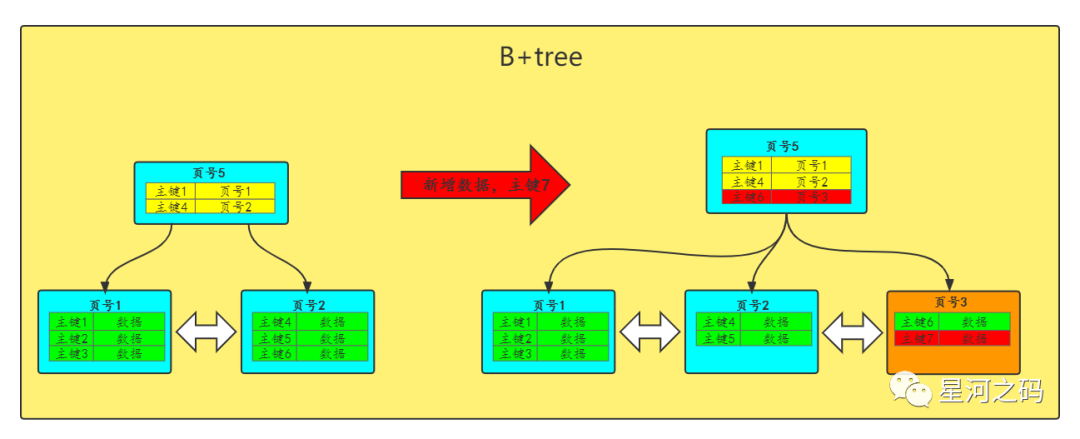
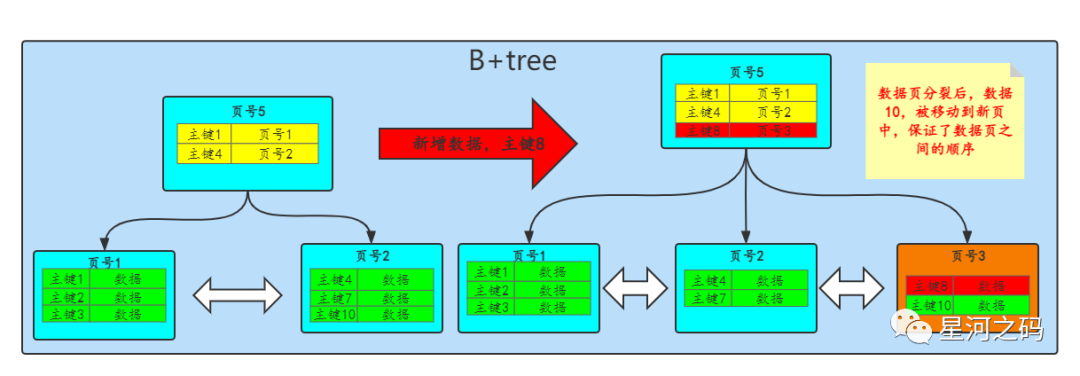
这里可能会有点疑惑,为什么会将数据页2中原本的数据(主键为6)也放在新的数据页3中?这个其实就是B+tree的一个「数据页分裂问题」。
❝
如上图:「当我们对数据页进行分裂后,会将数据10移动到新的数据页中,从而保证前后数据页之间的顺序性,以此保证主键索引在数据页中总是递增的」。
❞这里可能会有一个疑问,为啥不将数据8放在数据页2中,而是空出一个?我认为有两个原因:
第一:如果将数据8放在数据页2中,「当数据页足够多时,是否要判断将数据页10放在另一个已存在的数据页中,而不是新增数据页,以此类推,直到最后一个数据页」,这样无疑会非常的繁琐,相当于遍历剩余所有数据页和数据。这肯定是不可取的。
第二:将数据页2空出来了,下次如果有新的数据插入,假设这个数据介于7和8之间,那么它就可以直接插入,不必在新增数据页。
「在之前的《索引基础知识回顾》一文中提到索引是排序过的,并且在InnoDB中主键索引是递增的,在这种情况下,即使数据页不分裂也可以构建完整的B+Tree结构」。但是如果主键索引是自定义的,那就不能保证一定是自增的(UUID),这种情况过不分裂,「就有可能会出现后一个数据页中的所有行并不一定比前一个数据页中的行的id大」,如下
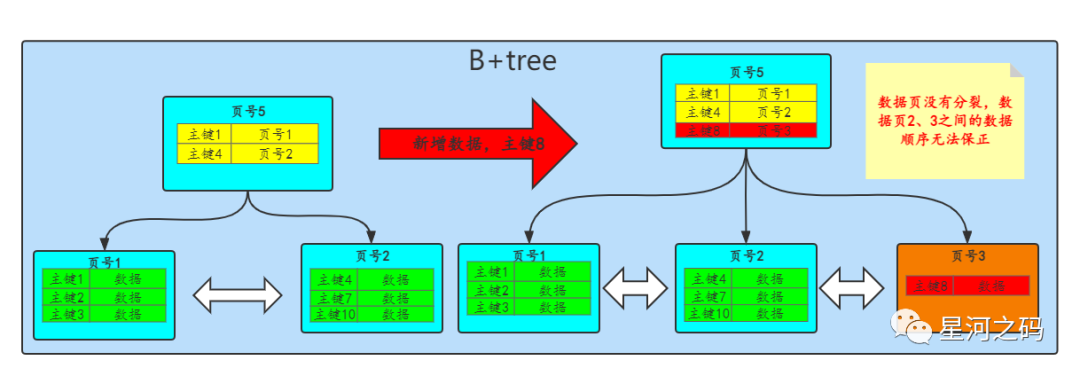
❝
如图,不分裂的情况下,数据页的主键8是小于数据页2的主键10的,所以这就会导致我们的数据乱掉。索引排序也就失效了
❞「页分裂的目的:保证后一个数据页中的所有行主键值比前一个数据页中主键值大」。
「叶子结点和非叶子结点都满了」
这种情况同样也需要进行数据页分裂,而且叶子和非叶子结点都要拆裂
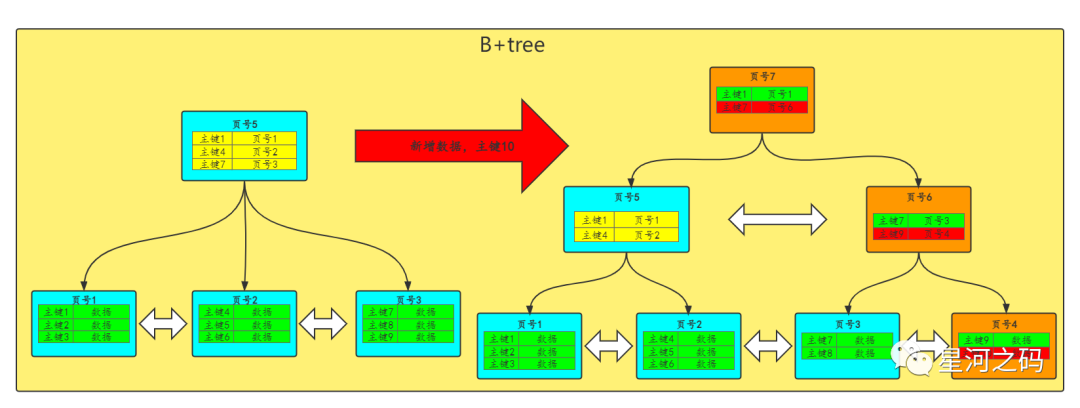
「叶子结点数据页分裂,新增一个数据页,将数据均分到两个数据页中」。 「非叶子结点数据页分裂,将数据页指针信息均分到两个数据页中,并且往上再加一层索引」。
3.3 InnoDB为什么使用B+树而不使用跳表
通过上述分析, 现在可以来看看为什么InnoDB为什么使用B+树而不使用跳表了,还是回到上面说读写两个方向来看:
「写入的效率」
总结一下跳表写入与B+Tree写入,其实方式上有点类似
❝
「在写入时,由于B+Tree需要分裂合并索引数据页,以及调整二叉树,维持平衡」;
「跳表却是独立插入,且根据随机函数确定层数,没有旋转和维持平衡的开销,因此跳表的写入性能会比B+树要好。」
❞「都是最底层存放数据,上层存索引」。 「写入数据时,都有可能会更新索引层,甚至增大层高」。 「查询的效率」
在之前的《单表最大2000W行数据》文中解释了「三层的B+Tree就可以存储2000W的数据,查找数据最多只需要三次磁盘IO即可」。
「跳表是链表结构,并且通过二分查找的方式去查找数据,当存储2000W数据并且满足二分查找时,需要24层索引,24层索引分散在不同的数据页中,查找数据最多会有24次磁盘IO」。
「结论」
「磁盘IO是非常慢的,3次IO的效率远远高于24次,也就是说B+Tree的查找效率远远高于跳表,虽然跳表写入的效率比B+Tree高,但是根据【二八原则】,系统写入的频率远低于读取,因此InnoDB最终选择使用B+树而不是跳表」。
❝
上面的【二八原则】可能不一定准确,但是当我们真的有系统的写频率超过读的频率的时候,也可以不用InnoDB引擎,使用其他的存储引擎也是一样的,具体还是要看应用场景。
❞「跳表写入效率比B+Tree高。而读取效率主要受限于磁盘IO的效率,因此Redis的有序集合Zset就是基于链表实现的,因为Redis 是纯内存数据库,压根就不需要操作磁盘,B+Tree的低层级、仅3次IO的优势就体现不出来了」。








