引言

Levenshtein 距离是衡量两个字符串距离的基本度量算法，对字符串的度量要求满足三角不等式^[1]（z ≤ x+y），例如，字符串“Sam”和“Samuel” 可以被认为是近似值。

在 Elasticsearch 所实现的模糊查询中，Levenshtein distance（莱文斯坦距离）是计算两个词项之间编辑距离的基本计算方法，比如以下几种情况均为Levenshtein 计算距离的基本情况：

•    混淆字符 (box → fox)•    缺少字符 (black → lack)•    多出字符 (sic → sick)•    颠倒次序 (act → cat)

1、Elasticsearch 中的模糊查询

举个最常见 的例子，当我们在搜索引擎中搜索“Elasticsearch”，但可能是由于有意或无意的原因，在输入的时候产生了拼写错误，而造成了拼写错误，错误的情况可能是以上四种情况之一，也可能同时包含多种情况，但是搜索引擎依然能为我们匹配到正确的相关结果：

2、距离计算

这种“智能纠错”的功能在 Elasticsearch 是如何实现的呢？

在 Lucene中，使用距离计算公式为 Levenshtein 距离，以下为 a，b 之间的 Levenshtein 距离长度 lev(a,b)，其计算公式为：

例如，“kitten”和“sitting”之间的 Levenshtein 距离为 3，因为以下 3 次编辑将一个更改为另一个，并且少于 3 次编辑没有办法做到这一点：

1. k itten → s itten（用“s”代替“k”），

2. sitt e n → sitt i n（用“i”代替“e”），

3. sittin → sitting（在末尾插入“g”）。

递归实现

这种实现非常低效，因为它多次重新计算相同子序列的 Levenshtein 距离。

更有效的方法永远不会重复相同的距离计算。比如，所有可能前缀的 Levenshtein 距离可能存储在一个数组中 M，并且M[i][j]是字符串 s 的最后 i 个字符与字符串 t 的最后 j 个字符之间的距离。表格很容易从第 0 行开始一次构建一行。当整个表格构建完成后，所需的距离是在表格中的最后一行和最后一列，表示所有字符s
与所有字符之间的距离中的字符t
。

全矩阵迭代法

通过保存第一个字符串的所有前缀和第二个字符串的所有前缀之间的 Levenshtein 距离，可以以动态编程方式计算矩阵中的值，并且因此找到两个完整字符串之间的距离作为计算的最后一个值。

伪代码实现：返回长度为 m 的字符串 s 和长度为 n 的字符串 t 之间的 Levenshtein 距离

3、Damerau–Levenshtein distance

Elasticsearch采用基于Levenshtein改进的 Damerau-Levenshtein 距离计算公式，与 Lucene 中的 Levenshtein 距离的不同之处在于，除了三个经典的单字符编辑操作（插入、删除和替换）之外，它还允许在其允许的操作中包含换位。

比如：axe => aex，两个字符串的容错距离为：Levenshtein = 2，而 Damerau-Levenshtein = 1。

在 Damerau-Levenshtein 中，a，b 两个字符串之间的距离计算公式 d_a，b（i，j）为：

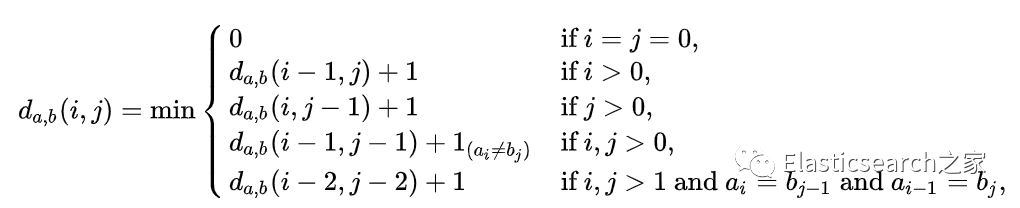
每个递归调用都匹配 Damerau-Levenshtein 距离所涵盖的一种情况：

•  d_a，b（i-1，j）+1 对应删除（从a到b）

   •  d_a，b（i，j-1）+1 对应插入（从a到b） 

   •  d_a，b（i-1，j-1）+ 1（a_i≠b_j）对应匹配或不匹配，取决于各自的符号是否相同   •  d_a，b（i-2，j-2）+ 1对应于两个连续符号之间的调换。

这里介绍两种算法：

第一种，计算所谓的最佳字符串对齐距离或受限编辑距离，伪代码实现：

与 Levenshtein 距离算法的不同之处在于增加了一个递归：

第二种，计算具有相邻换位的 Damerau-Levenshtein 距离。两种算法之间的区别在于，最优字符串对齐算法计算在没有子字符串被多次编辑的情况下使字符串相等所需的编辑操作数，而第二种算法则没有这样的限制。伪代码实现：

以CA和ABC之间的编辑距离为例。Damerau-Levenshtein 距离 LD( CA , ABC ) = 2 因为 CA → AC → ABC，但最优字符串对齐距离 OSA( CA , ABC ) = 3 因为如果使用操作CA → AC则无法使用AC → ABC因为这需要多次编辑子字符串，这在 OSA 中是不允许的，因此最短的操作序列是CA → A → AB →美国广播公司。请注意，对于最佳字符串对齐距离，三角不等式不成立：OSA( CA , AC ) + OSA( AC , ABC ) < OSA( CA , ABC )，因此它不是真正的衡量标准。

不当你的世界  只做你的肩膀

○

无畏的太阳

○

心情|阅读|鸡汤|电影|牢骚

请留下你指尖的温度

让太阳拥抱你

记得这是一个有温度的公众号

References

[1]
 三角不等式: https://en.wikipedia.org/wiki/Triangle_inequality