原文链接: http://tecdat.cn/?p=14200
之前我们在关于投资组合优化相关的内容中已经看到了Markowitz的理论,其中给出了预期收益和协方差矩阵
> pzoo = zoo ( StockIndex , order.by = rownames ( StockIndex ) )
> rzoo = ( pzoo / lag ( pzoo , k = -1) - 1 ) * 100
>
ans <- do.call ( method , list ( x = x , ... ) ) + return ( getCov ( ans ) )} > covmat=Moments(as.matrix(rzoo),"CovClassic")
> (covmat=round(covmat,1))
SP500 N225 FTSE100 CAC40 GDAX HSI
SP500 17.8 12.7 13.8 17.8 19.5 18.9
N225 12.7 36.6 10.8 15.0 16.2 16.7
FTSE100 13.8 10.8 17.3 18.8 19.4 19.1
CAC40 17.8 15.0 18.8 30.9 29.9 22.8
GDAX 19.5 16.2 19.4 29.9 38.0 26.1
HSI 18.9 16.7 19.1 22.8 26.1 58.1
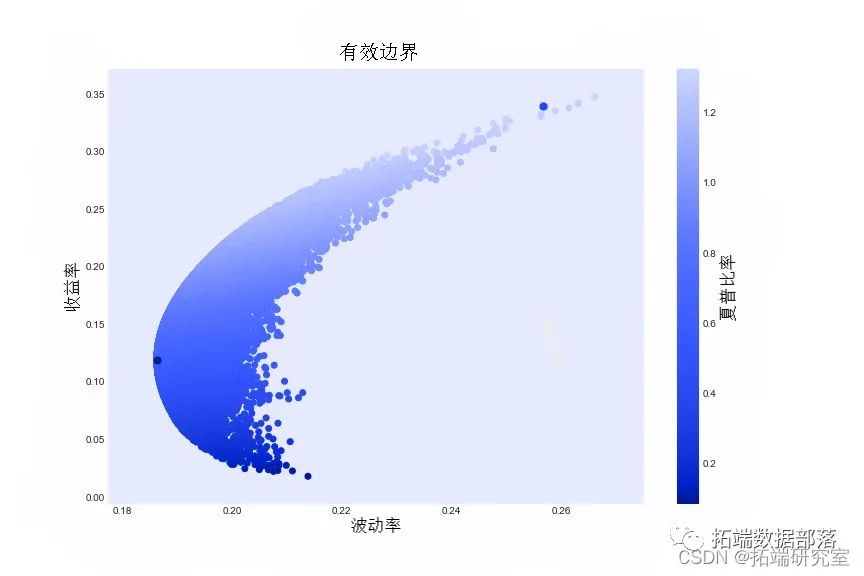
现在,我们可以可视化下面的有效边界(和可接受的投资组合)
> points(sqrt(diag(covmat)),er,pch=19,col="blue")
> text(sqrt(diag(covmat)),er,names(er),pos=4, col="blue",cex=.6)
> polygon(u,v,border=NA,col=rgb(0,0,1,.3))
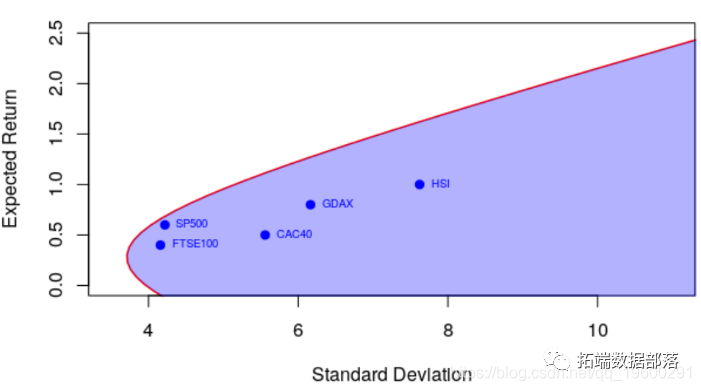
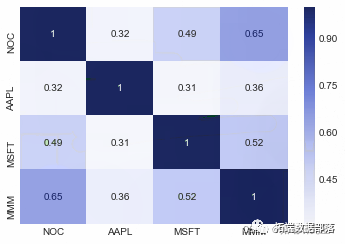
实际上很难在该图上将重要的东西可视化:收益之间的相关性。它不是点(单变量,具有预期收益和标准差),而是有效边界。例如,这是我们的相关矩阵
点击标题查阅往期内容


左右滑动查看更多

SP500 N225 FTSE100 CAC40 GDAX HSI
SP500 1.00 0.50 0.79 0.76 0.75 0.59
N225 0.50 1.00 0.43 0.45 0.43 0.36
FTSE100 0.79 0.43 1.00 0.81 0.76 0.60
CAC40 0.76 0.45 0.81 1.00 0.87 0.54
GDAX 0.75 0.43 0.76 0.87 1.00 0.56
HSI 0.59 0.36 0.60 0.54 0.56 1.00
我们实际上可以更改FT500和FTSE100之间的相关性(此处为.786)
courbe=function(r=.786){
ef
plot(ef$sd,ef$er,type="l",xlab="Standard Deviation",ylab="Expected Return",
points(sqrt(diag(covmat)),er,pch=19,col=c("blue","red")\[c(2,1,2,1,1,1)\])
polygon(u,v,border=NA,col=rgb(0,0,1,.3))
}
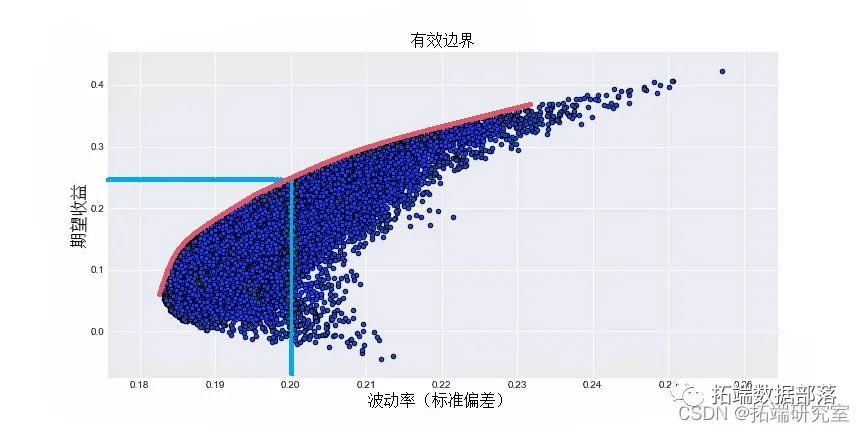
例如,相关系数为0.6,我们得到以下有效边界
> courbe(.6)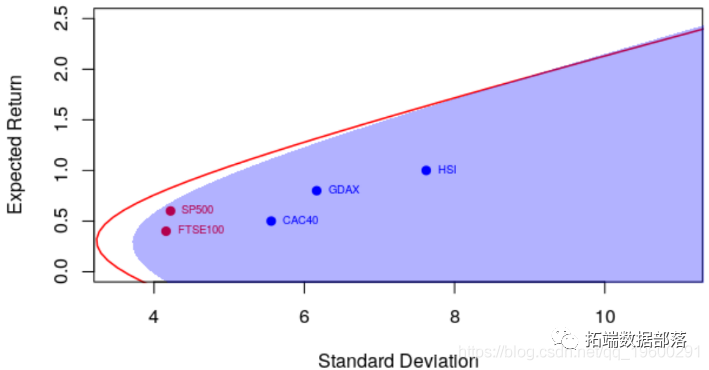
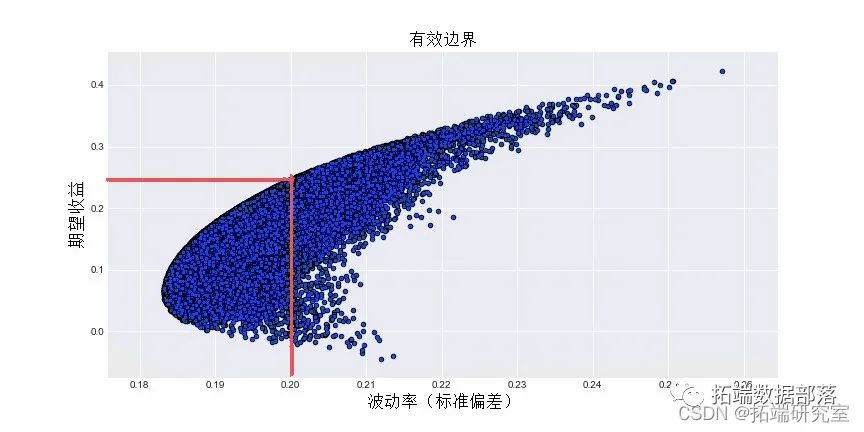
并具有更强的相关性
> courbe(.9)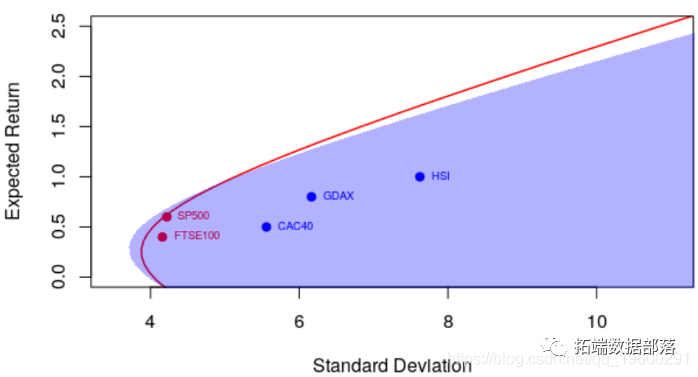
很明显,相关性很重要。但更重要的是,期望收益和协方差不是给出而是估计的。以前,我们确实将标准估计量用于方差矩阵。但是可以考虑使用另一个更可靠的估计器
covmat=Moments(as.matrix(rzoo),"CovSde")
points(sqrt(diag(covmat)),er,pch=19,col="blue")
text(sqrt(diag(covmat)),er,names(er),pos=4,col="blue",cex=.6)
polygon(u,v,border=NA,col=rgb(0,0,1,.3))
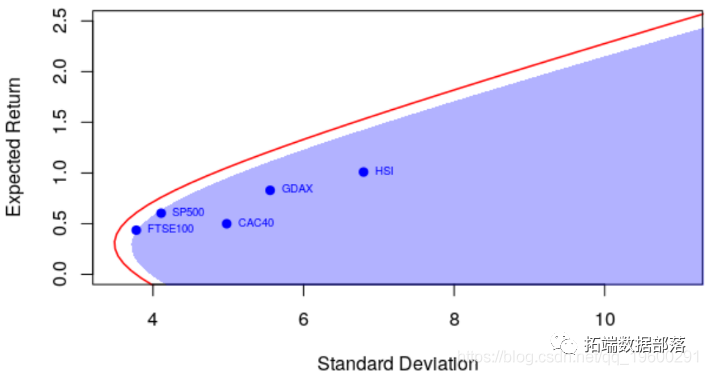
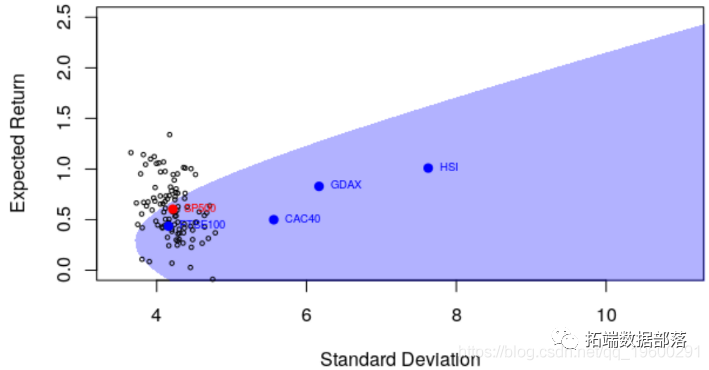
它确实影响了点的(水平)位置,因为方差现在以及有效边界都不同,而方差明显更低。
为了说明最后一点,说明我们确实有基于观察到的收益的估计量,如果我们观察到不同的收益怎么办?了解可能发生的情况的一种方法是使用引导程序,例如每日收益。
> plot(ef$sd,ef$er,type="l",xlab="Standard Deviation",ylab="Expected Return", xlim=c(3.5,11),ylim=c(0,2.5),col="white",lwd=1.5)
> polygon(u,v,border=NA,col=rgb(0,0,1,.3))
> for(i in 1:100){
+
+
+ er=apply(as.matrix(rzoo)\[id,\],2,mean)
+ points(sqrt(diag(covmat))\[k\],er\[k\],cex=.5)
+ }
或其他资产
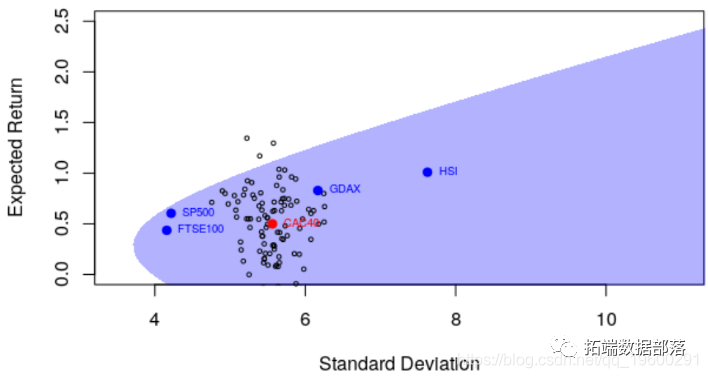
这是我们在(估计的)有效边界上得到的
> polygon(u,v,border=NA,col=rgb(0,0,1,.3))
> for(i in 1:100){
+
+
+
+ ef <- efficient.frontier(er, covmat, alpha.min=-2.5, alpha.max=2.5, nport=50)
+ lines(ef$sd,ef$er,col="red")
+ }
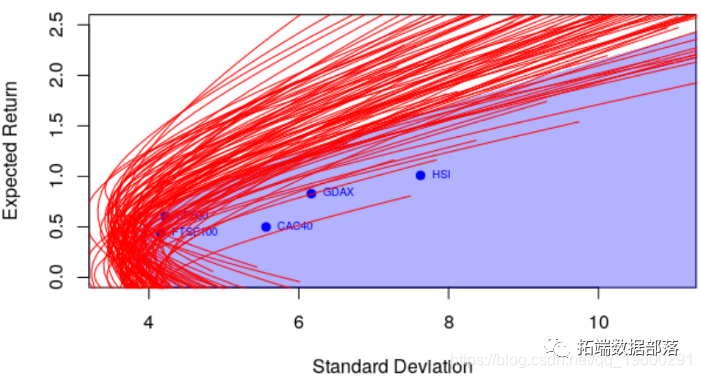
因此,至少在统计学的角度上,要评估一个投资组合是否最优是很困难的。

点击文末“阅读原文”
获取全文完整资料。
本文选自《R语言Markowitz马克维茨投资组合理论分析和可视化》。
点击标题查阅往期内容



文章转载自拓端数据部落,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。