算法-排序系列02之冒泡排序

冒泡排序

基本思想

每次都操作两个相邻的数据.每次冒泡操作都对相邻的两个数据进行比较,看是否满足大小关系要求,如果不满足,就进行互换。每次冒泡都会冒出一个最小/大值，并移动到它应该在的位置.重复 n 次,就完成了对 n 个数据的排序工作.

排序逻辑图

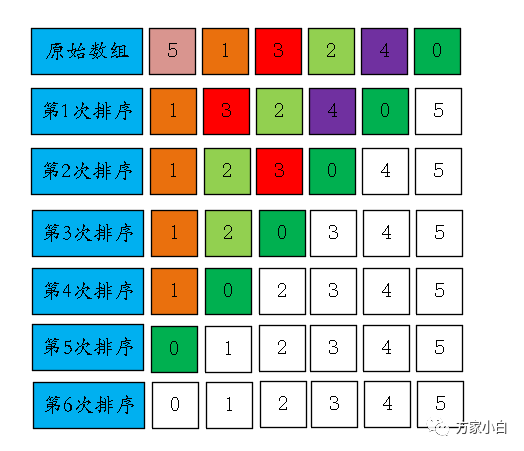
这里在详细的写一下第一次排序的过程：

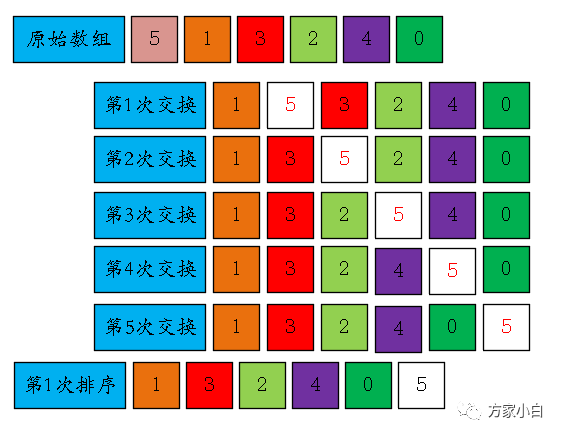
按照以上逻辑的代码实现

算法实现

int *bubble_sort(int *a, int length) {

    for (int i = 0; i < length; i++) {
        for (int j = 1; j < length-i; j++) {
            if (a[j - 1] > a[j]) {
                int temp = a[j - 1];
                a[j - 1] = a[j];
                a[j] = temp;
            }
        }
        // print(a, length);
    }
    return a;
}

这种实现，在这种情景下，就会浪费时间。

如果原始数组为:

[5,0,1,2,3,4]

排序过程如下:

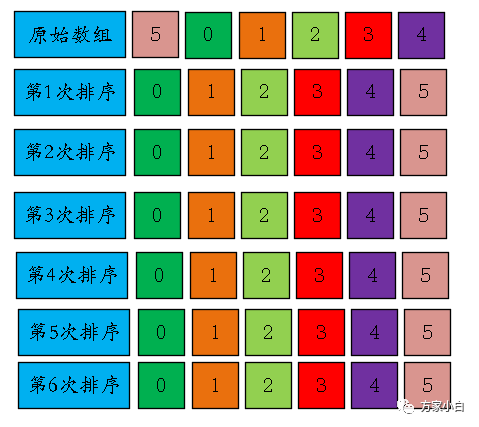
可以发现,在完成第一趟排序的时候，实际上已经是正确的排序结果了.我们可以采用下面的方式进行优化

int* bubble_sort(int *a, int length){

    for (int i = 0; i < length; i++) {
        int flag = 0;
        for (int j = 1; j < length - i; j++) {
            if (a[j - 1] > a[j]) {
                int temp = a[j - 1];
                a[j - 1] = a[j];
                a[j] = temp;
                flag = 1;
            }
        }
        if (!flag) {
            break;
        }
        //print(a, length);
    }
    return a;
}

从上面的代码可以看出:

• 冒泡排序是基于比较,交换的排序算法。

• 冒泡排序使用的空间复杂度为O(1),是一个原地排序算法。

• 以上代码实现的冒泡算法是稳定的排序算法. if(a[i]<=a[j])
  就是一个不稳定的排序算法了.

• 冒泡算法最好情况下的时间复杂度是O(n),最坏情况下的时间复杂度是O(n2). 那平均情况下的时间复杂度怎么计算呢?

计算平均情况下的时间复杂度

这里，我们引入三个概念

• 有序元素对: 如果 i<j
  ,并且 a[i]<a[j]
  ,那么这个一对儿数就是有序的。

• 逆序元素对: 如果 i<j
  ,并且 a[i]>a[j]
  ,那么这个一对儿数就是逆序的。

• 有序度: 数组中具有有序关系的元素对的个数.

• 满有序度: 完全有序的数列。

其中 满有序度
= 有序度
+ 逆序度
。

举个例子:

[4,5,6,3,2,1]

有序度为 3,也称为 原始有序度, 分别为: (4,5)
(4,6)
(5,6)

满有序度为 2n∗(n−1)=15

冒泡排序中包含两个操作原子,比较和交换.没交换一次，有序度就会加 1. 所以，交换次数，就是逆有序度。那么，逆有序度 = 满有序度 - 初始有序度
. 也就是: 15 - 3 = 12. 需要进行 12 次操作。

平均情况下，要进行4n∗(n−1)次操作. 比较操作肯定要比交换操作多，而最坏情况下的时间复杂度就是 O(n2), 所以平均情况下的时间复杂度就是 O(n2)