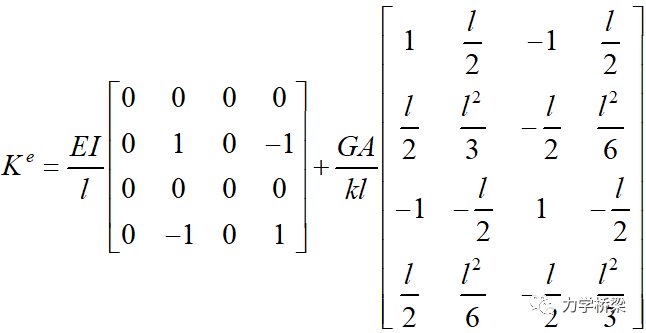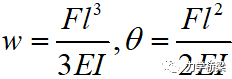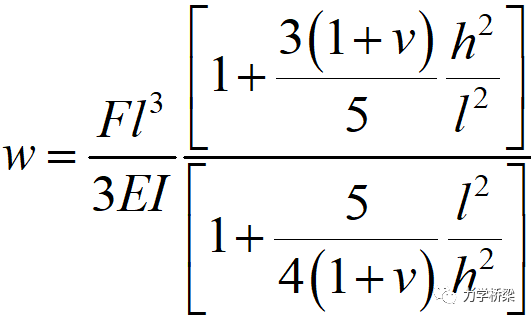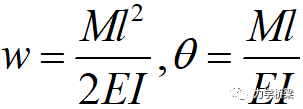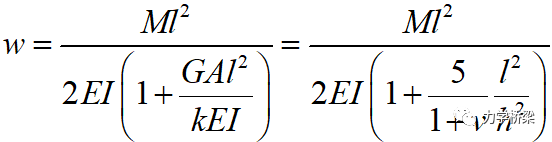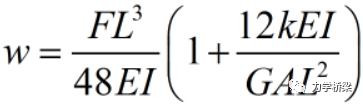[前述]
伯努利梁(Euler-Bernoulli Beam)和铁木辛柯梁(Timoshenko Beam)通常我们不怎么去区分,建模的时候也很少去考虑究竟用何种梁单元。本文将从两种梁单元的本质出发,并结合有限元理论去探讨两种梁单元之间的区别。
伯努利梁的一个非常重要的假定为平截面假定。平截面假定指梁在变形过程中横断面仍保持原来的平面,且与对应位置的梁轴线切线垂直。共传递两个关键信息:
1.梁变形过程中横断面为刚性平面,即不会随竖向荷载而发生畸变;
梁受弯后变形前后梁截面仍然保持原有的截面形状和尺寸,即截面上各点的相对位置关系不变。同时由于横断面与梁轴线垂直,那么梁轴线的切线角度即为梁截面的转动角度。在小变形范围内,梁截面各点的纵向位移即为转动角度乘上其距梁轴线的距离。具体公式推导如下。


从以上的推导分析来看,平截面假定隐含了一个条件:梁单元的剪切应变为0,即不考虑剪切变形的影响。平常我们进行计算分析的时候一般都是采用伯努利梁。伯努利梁可模拟刚性移动、刚性转动、纯弯曲,但是不能模拟纯剪切!当我们用伯努利梁进行计算时,通常剪应力均是根据剪力再按照截面特性进行计算的。铁木辛柯梁算是改进版的伯努利梁,其在伯努利梁的基础上考虑了剪切变形。对平截面假定进行了略微调整。铁木辛柯梁认为在外荷载作用下,变形前垂直于中面的截面变形后不再保持垂直。这是因为梁内的横向剪切力产生的剪切变形引起了附加挠度。图示如下。
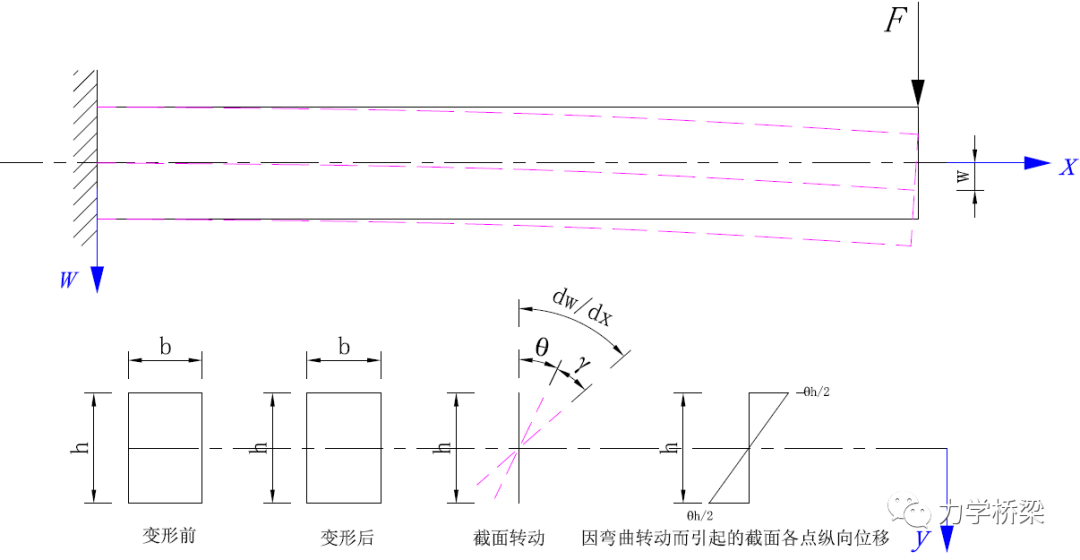
此时,梁截面各点的纵向应变不再与梁轴线的切线斜率呈正比关系,而是需要将剪切变形引起的转动量去除后才是弯曲转动引起的量,可以看成叠加原理的一个运用。具体公式推导如下所示。(本次推导采用挠度和转角分开进行插值)

故而,铁木辛柯梁单元刚度矩阵如下:
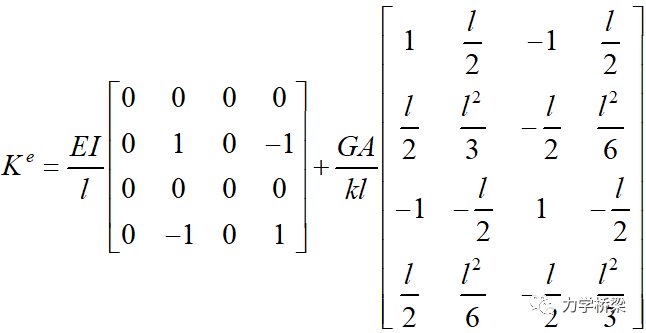
这里说一下剪切应变能中为什么会有系数k。系数k指截面剪切校正因子。因为梁弯曲过程中截面为平面,也就是剪应力和剪应变在截面上是均匀分布的。但是实际剪应力和剪应变在截面上不是均匀分布的,而是抛物线分布的,在中面达到最大值,在上下表面等于0。所以需要引入校正因子k对剪切应变能进行修正。k有不同的计算方法。一种理论是认为剪应力取截面实际剪应力的平均值,据此,矩形截面k=3/2,圆形截面k=4/3。另一种理论认为应使得应变能等效一致。据此,矩形截面k=6/5,圆形截面k=10/9。有限元中通常采用能量等效方法。
考虑一悬臂梁长L,弹性模量为E,在悬臂端作用一集中力F和一集中弯矩M,截面为矩形,宽×高=b×h。分别求伯努利梁和铁木辛柯梁在两种荷载下挠度与转角之间的关系。结构图示如下。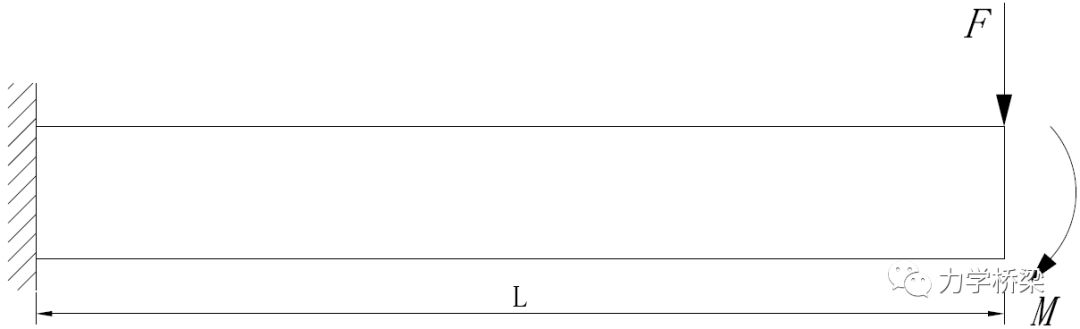
[单独集中荷载下]
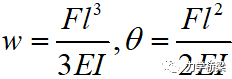
铁木辛柯梁求得的悬臂端挠度如下:
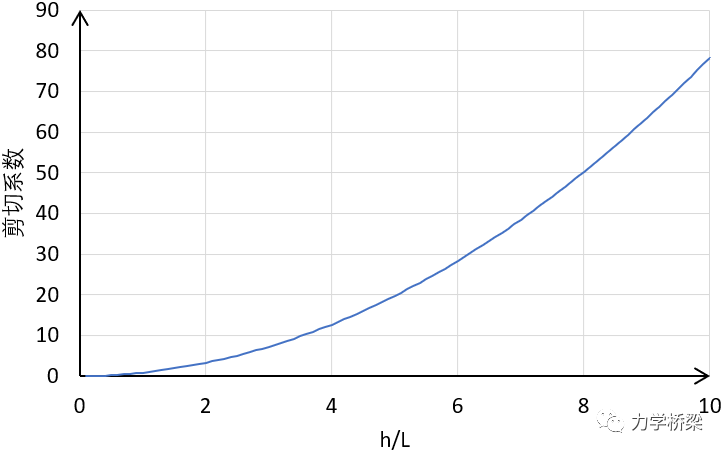
由上可知,铁木辛柯梁在集中荷载作用下挠度多了一项系数,当高跨比h/L趋向0时,即往薄梁靠近,分子趋向于1,但是分母却却趋向于∞。说明精确积分下产生了剪切锁死现象。取泊松比v=0.3,h/L=0.1,则该系数为0.01,与伯努利梁计算值相差近100倍!!!
上图说明在精确积分下,高跨比的影响呈指数型分布!且当梁越薄时其计算异常越大。说明当进行计算的时候,一阶构造函数下的精确积分铁木辛柯梁精度欠缺。
[单独弯矩荷载下]
伯努利梁求得的悬臂端挠度和转角如下:
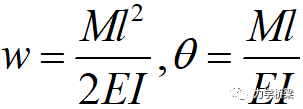
铁木辛柯梁求得的悬臂端挠度如下:
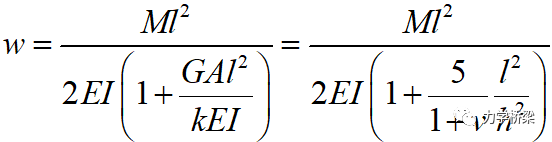
可见精确积分下挠度仍会出现h/L的系数,说明当h/L趋向于0时,结构将会出现剪切锁死。从单元刚度矩阵也可得,2节点铁木辛柯梁单元不能描述纯弯曲状态。如若采用,应当采用3节点铁木辛柯梁。
[对比小节]
从上述的对比分析看,2节点铁木辛柯梁会出现剪切锁死现象,从而导致计算异常,建议在建模计算中采用2节点伯努利梁或者3节点铁木辛柯梁。本例中的对比分析仅是从有限元角度去对比的,并不是说铁木辛柯梁本身计算精度低于伯努利梁。由于单元刚度矩阵插值函数的构造方式不同,阶数不同,才导致铁木辛柯梁出现计算精度异常的现象。
剪切锁死可以采取缩减积分和增加梁单元数,也可以改善2节点铁木辛柯梁的计算精度。也可以通过改变挠度插值函数的构造方法,从而从根源解决剪切锁死。换句话说,剪切锁死并不是铁木辛柯梁的“固有特性”,而是因为离散单元的插值构造函数本身阶数存在不足以描述纯弯曲状态导致的。《公路钢筋混凝土及预应力混凝土桥涵设计规范》(2018)第8.4.2条中认为高跨比h/L<0.2或者跨高比L/h>5.0时为伯努利梁。后附简支梁均布荷载、跨中集中荷载下跨中挠度铁木辛柯梁的理论计算值。
简支梁均布荷载:

简支梁跨中集中荷载:
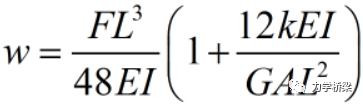
说明考虑剪切变形其挠度会偏大。