作为一个MATLAB小白,每次遇到需要用MATLAB分析的问题,都抱着侥幸心理绕道而走。最近,避无可避,迟到的终究还是来了。频率响应的重要性不必多说,这里把用MATLAB做频率响应的方法简单记录一下。

首先是要在MATLAB中输入传递函数表达式。对于最常用的分式传递函数可以用tf()函数输入。然后直接用margin()函数可以直接得到频率响应。本例的传输函数如下图所示。
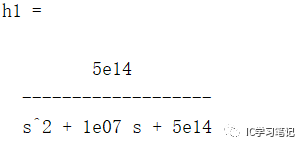
频率响应,显然是一个低通特性
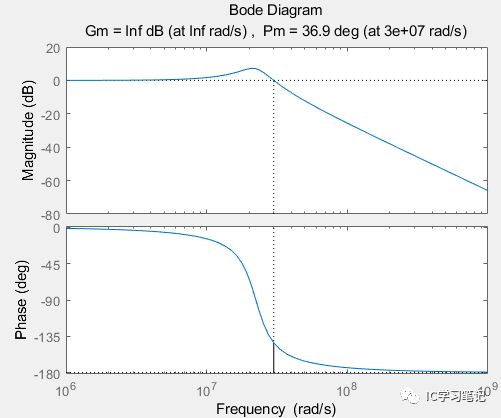
第二种传输函数的输入方法是,用我们平时手算习惯用的拉普拉斯表达式,如图,两种方法的到的结果是一样的。

但是第二种方法适用于所有形式的传输函数,例如针对下例的传输函数
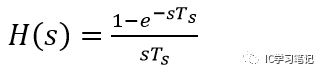
s项在指数里面,就没法用第一种传输函数的输入方法。
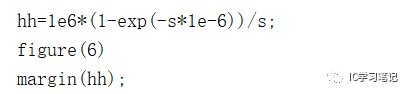
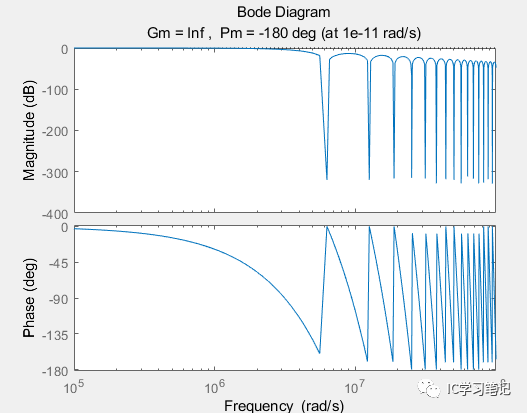
频率响应是频域特性,通常除了考查频率特性外,我们还要看时域特性。常用的有阶跃响应和冲击响应。MATLAB中用step()和impulse()函数可以直接得到结果。



另外,除了以上用MATLAB自带的函数求频率响应外,还可以用s=jw,再求模得到幅频响应。

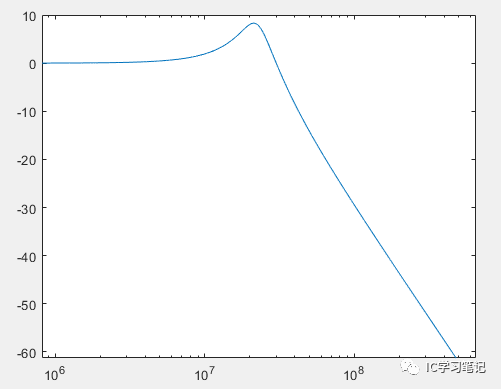
得到的结果相同。
%源码%
h=tf([5e14],[1 1e7 5e14]); %第一种传输函数表达式,针对s的多次幂分式
h1=h %重新赋值h,可以在命令行窗口显示传输函数
figure(1)
margin(h); %频率响应
s=tf('s');
H=5e14/(s^2+1e7*s+5e14); %第二种传输函数表达式,所有表达式都可用
figure(2)
margin(H); %两种表达式最后出来的结果一致
t=0:1e-8:1.5e-6;
figure(3)
step(H,t); %阶跃响应
figure(4)
impulse(H,t); %冲击响应
f=1:1e3:1e8;
w=2*pi*f;
F=5e14./((j*w).^2+1e7*(j*w)+5e14); %也可以用s=jw,再求模得到幅频响应
figure(5)
semilogx(w,10*log(abs(F)));
hh=1e6*(1-exp(-s*1e-6))/s;
figure(6)
margin(hh);






