文章信息
「来源」：Proceedings of the 39th International Conference on Machine Learning（ICML） 2022
「标题」：Scalable Deep Gaussian Markov Random Fields for General Graphs
「作者」：Joel Oskarsson, Per Sidén, Fredrik Lindsten
「链接」：https://proceedings.mlr.press/v162/oskarsson22a.html
内容简介
图是科学建模中非常重要的结构。图上的机器学习方法已被证明在许多应用中很有用，因为它们能够处理一般结构化的数据。在这个领域，发现了概率图模型，另一个较新的基于图的模型系列是图神经网络 (GNN)。将统计上合理的方法与深度学习相结合是基于图的方法领域和整个现代机器学习的一个重要目标。
因此十分有必要去设计一种具有强大统计基础且具有GNN可扩展性的方法。虽然一些图（例如描述分子的图）相对较小，但社交网络和交通网络中会出现大量图。在许多情况下，不仅需要产生准确的预测，还需要对预测的不确定性进行某种度量。「贝叶斯方法提供了一种获得预测不确定性估计的原则方法，该方法可以正确解释潜在变量中的不确定性」。一种利用图稀疏性的贝叶斯模型是高斯马尔可夫随机场 (GMRFs)。高斯马尔可夫随机场(GMRFs)框架提供了一种利用其稀疏结构在图上定义高斯模型的原则方法。Sid ́ en 和 Lindsten (2020) 的 Deep GMRF (DGMRF) 框架结合了具有卷积神经网络 (CNN) 的GMRFs，用于图像结构化数据的特殊情况。DGMRFs可以有效地训练并保留GMRFs的所有有用属性，例如潜在场的精确贝叶斯推理。基于深度GMRF的多层结构的通用图，本文提出了一种最初仅针对格图的灵活的GMRF模型。通过设计一种新型层，模型能够扩展到大图。该层的构造允许使用变分推理和用于图神经网络的现有软件框架进行有效训练。通过在许多合成和现实世界数据集上的实验，所提出模型的有用性得到了验证，即在这些数据集上，它与其他贝叶斯和深度学习方法相比具有优势。
本文的主要贡献如下：
通过设计一种基于GNN的新型层结构，将DGMRF框架扩展到一般图。 利用改进的变分分布使DGMRF训练适应这种新设置。 提出了可扩展的方法，以执行对训练至关重要的对数行列式计算。 在合成数据上展示了所得模型的属性。 在多个真实世界的数据集上进行实验，发现本文提出的模型优于现有方法。
相关理论与技术
高斯马尔可夫随机场(GMRFs)
在图模型中，一组随机变量与图的节点相关联。GMRFs是无向图模型，其中节点共同遵循高斯分布。更具体地说，让是一个无向图，其中N个节点连接在随机向量 中,其均值为，精度矩阵为。GMRF是一个多元高斯，其精度矩阵与图一样稀疏。但是请注意，协方差矩阵仍然可以是完全密集的，从而在图中的所有节点之间启用依赖关系。
深度高斯马尔可夫随机场(DGMRFs)
对于仿射图 ，Sid ́ en和Lindsten将GMRF 定义为：
其中 是一个矩阵，是一个偏移向量。这导致GMRF的平均值 和精度矩阵 。上述公式使隐式定义，不同于将高斯噪声映射到数据的其他生成模型的设置。
方法介绍
本文将DGMRF框架扩展到一般图，消除了格图的假设以匹配GMRF的一般定义。为了实现这一点，本文设计了一种新型层，而不对图结构做任何假设。接着提出了一种使用可扩展对数行列式计算和新的、更灵活的变分分布来训练这种新型DGMRF的方法。模型概述如图 2 所示。
图层
将 Sid ́ en 和 Lindsten (2020) 的基于 CNN 的 DGMRF 层推广到一般图需要一些特殊考虑。其中，考虑图中不同的节点度是不可或缺的。为了实现这一点， 本文提出的层定义为：
变分训练
DGMRF的参数可以通过最大化
来训练。然而，这通常是不可行的，因为它需要计算后验精度矩阵的行列式。对于较大的N，可以使用变分推断，最大化证据下界 (ELBO)：计算对数行列式
计算方程式中必要的对数行列式。基于CNN的DGMRF是在格图上定义的，它在上创建了一个特殊的结构，并允许为对数行列式找到有效的封闭式表达式。由于本文不对图结构做出任何此类假设，因此文本在这里提出了新的可扩展方法来计算对数行列式。
「特征值法」
「幂级数法」
实验分析
图DGMRF是使用PyTorch和PyTorch Geometric GNN库 (Fey & Lenssen, 2019) 实现的。本文在许多合成和现实世界的数据集上评估所提出的模型。对5个不同的随机种子重复所有DGMRF训练，并将DGMRF结果报告为这些种子的平均值。
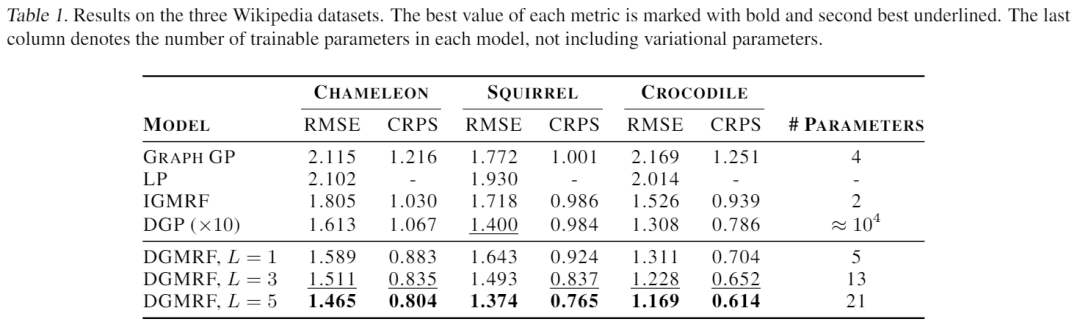维基百科图表上的DGMRFs和基线模型的结果如表1所示。就RMSE而言，1层DGMRF的性能与基线模型相似或更好。层数越多似乎越有益，因为在 时达到了最佳性能。值得注意的是，所考虑的图的直径约为10，这意味着5层的DGMRF对应于几乎完全密集的精度矩阵。通过接近精确的后验推断，DGMRF模型还给出了原则上的不确定性估计，这反映在有利的CRPS值中。
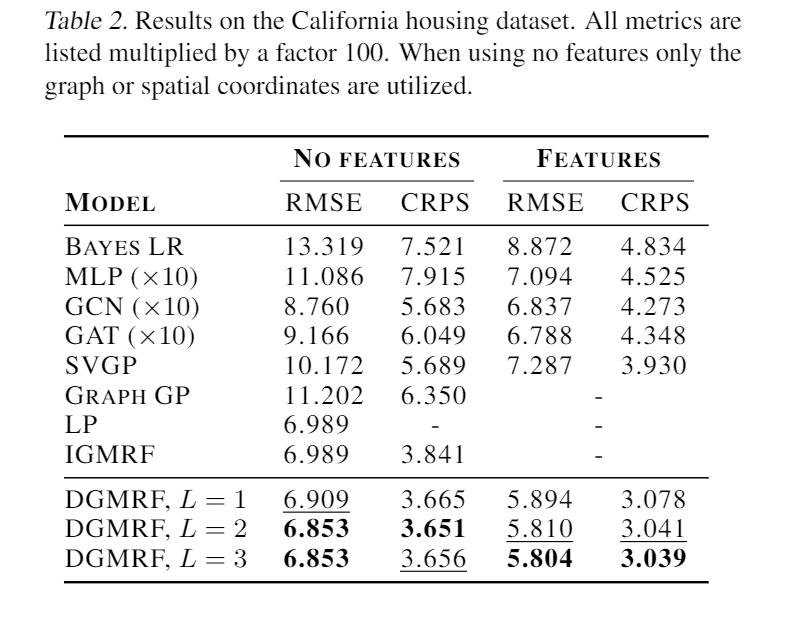在表2中，报告了使用和不使用节点特征的结果。结果展示了如何利用图结构和节点特征使本文的DGMRF能够准确地对数据进行建模。即使没有节点特征，本文的DGMRF的概率预测也会导致最低的CRPS。
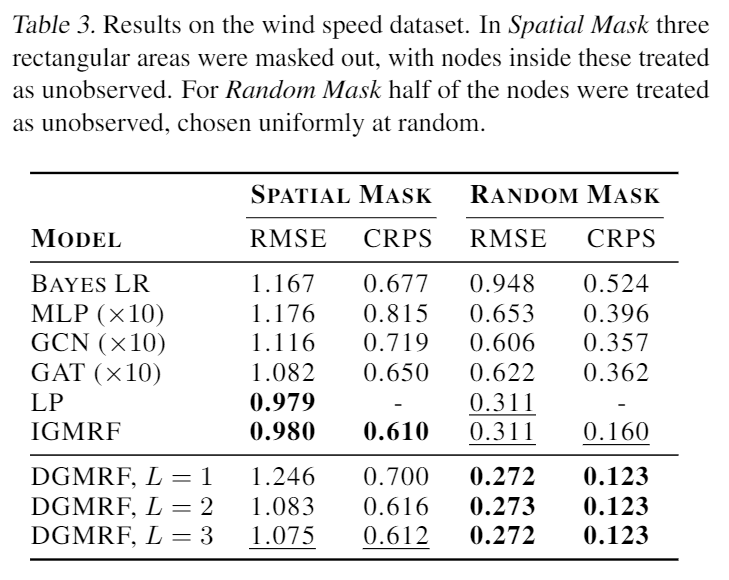风速数据集的结果如表3所示。实验展示了本文的模型在不牺牲预测性能的情况下扩展到大图的能力。
总结
本文介绍了「用于一般图」的「DGMRF」。通过「GNN的计算框架」和「可扩展的对数行列式计算」，该模型可以应用于大型图。在实验中，所提出的模型优于其他贝叶斯和深度学习方法。本文目前只考虑了高斯似然，但对非共轭设置的扩展可能很有趣（例如节点分类）。未来工作的其他方向包括更好的方法来利用节点特征和联合学习图结构的方法。
