ICML  2022 | A New Perspective on the Effects of Spectrum in Graph Neural Networks

“

文章信息

来源：Proceedings of the 39th International Conference on Machine Learning（ICML） 2022
标题：A New Perspective on the Effects of Spectrum in Graph Neural Networks
作者：Mingqi Yang, Yanming Shen, Rui Li, Heng Qi, Qiang Zhang, Baocai Yin
链接：https://proceedings.mlr.press/v162/yang22n.html
代码：https://github.com/qslim/gnn-spectrum

”

内容简介

GNN的许多改进可以看作是对底层图矩阵的谱的操作，这促使本文直接研究谱的特性及其对GNN性能的影响。通过对现有GNN体系结构的总结，本文发现由非光滑谱引起的相关性问题是GNN应用更强大的图滤波器和开发深层结构的障碍，从而制约了GNN的性能。受此启发，本文提出了无相关结构，它自然地消除了不同信道之间的相关性问题，使得在每个信道中使用更复杂的滤波器成为可能。最终的无相关结构与更强大的滤波器一致地提高了学习图表示的性能。

与图的谱相关联的相关分析进一步表明，相关问题本质上是由图的谱引起的。换句话说，对于谱不光滑的图拓扑，即使在浅层结构下也会出现这个问题，而深度模型进一步使谱不光滑，最终加剧了这个问题。同时，相关性分析也提供了一个统一的解释的有效性的各种现有的改进与图的频谱，因为他们都隐含地施加了一些限制频谱，以缓解相关性问题。然而，这些改进是在缓解相关性问题和应用更强大的图滤波器之间的折衷：由于滤波器实现直接反映在频谱上，针对相关信号模式的更合适的滤波器可能对应于不适定的频谱，这反过来不会获得性能改进。因此，在一般的GNN结构中，相关性问题成为应用更强大滤波器的障碍。虽然理论上可以通过增加多项式的阶数k来逼近更复杂的图滤波器（Shuman et al.，2013)，但在流行的模型中，简单滤波器，如低通滤波器（Kipf&Welling,2017；Wu et al.，2019)，或固定滤波器系数（Klicpera et al.，2019a；b）作为实际适用的选择。

有了以上的理解，关键的解决方案是将相关问题从滤波器设计中解耦，这就产生了本文的无相关结构。与现有方法相比，它允许专注于探索更复杂的过滤器，而不考虑相关性问题。有了这个保证，本文可以改进多项式滤波器的逼近能力，以更好地逼近所需的更复杂的滤波器（Hammond et al.，2011；Defferrard et al.，2016)。然而，本文也发现仅仅增加多项式基的个数是不能实现的，因为基的特征隐含地限制了多项式滤波器中可用基的个数。因此，常用的（归一化）邻接或拉普拉斯矩阵以其谱为基，不能有效地利用高阶基。为了解决这个问题，本文提出了新的图矩阵表示，它能够利用更多的基和可学习的滤波器系数来更好地响应更复杂的信号模式。所得到的模型显著提高了学习图表示的性能。尽管关于多项式滤波器的研究包括固定系数和可学习系数（Defferrard et al.，2016；Levie et al.，2019；Chien et al.，2021；He et al.，2021)，但就作者所知，他们都集中在系数设计上，并使用（归一化）邻接或拉普拉斯矩阵作为基础。因此，作者的工作与它们有很好的区别。

本文的主要贡献

• 证明了一般的GNN结构都存在相关问题，并用谱平滑性来量化这个问题；
• 提出了一种无相关的结构，将相关问题与图卷积解耦；
• 证明了谱特性也阻碍了多项式滤波器的逼近能力，并通过改变图的谱来解决这一问题。

相关工作

GNNS的许多改进可以统一到谱平滑操作中，如低通滤波器（Wu et al.，2019；Zhu et al.，2021；Klicpera et al.，2019a；B；Chien et al.，2021；Balcilar et al.，2021)、缓解过moothing（Ming Chen et al.，2020；Xu et al.，2018；Liu et al.，2020；Li et al.，2018)、图归一化（Cai et al.，2021)等，本文对相关问题与底层图矩阵谱关系的分析为它们的有效性提供了统一的解释。

Chebynet(Defferrard et al.，2016)、Caylenet(Levie et al.，2019)、Appnp(Klicpera et al.，2019a)、SSGC(Zhu&Koniusz，2020)、GPR(Chien et al.，2021)、Bernnet(He et al.，2021)等探索各种多项式滤波器，并使用归一化邻接或拉普拉斯矩阵作为基。通过改变滤波器基的谱来提高多项式滤波器的逼近能力。所得到的基允许利用更多的基来逼近更复杂的滤波器，并且更适合从头开始学习系数。

同时的工作（Jin et al.，2022)也指出了无限深度情况下的过相关问题，而没有进一步讨论这种现象背后的原因（如图的谱）。相反，本文指出相关性本质上是由底层图滤波器的谱不光滑引起的，并用谱光滑性来量化这种影响。它允许分析跨所有层的相关性，而不仅仅是理论上的无限深度。

无相关体系结构

从图的频谱角度进行相关性分析表明，在一般的GNN结构中，不光滑的频谱会导致相关问题，从而阻碍了深入结构的开发和利用更有表现力的图滤波器。可以定义为如下公式：

和 都是特征变换神经网络，分别具有可学习参数 和 。如下：

基于滤波器的光谱优化

人们可以直接对S的谱应用平滑函数，这有助于缩小特征值接近1或-1的范围。可以有各种方法来达到这一目的，在本文中提出了以下基于特征分解的对称矩阵的方法:

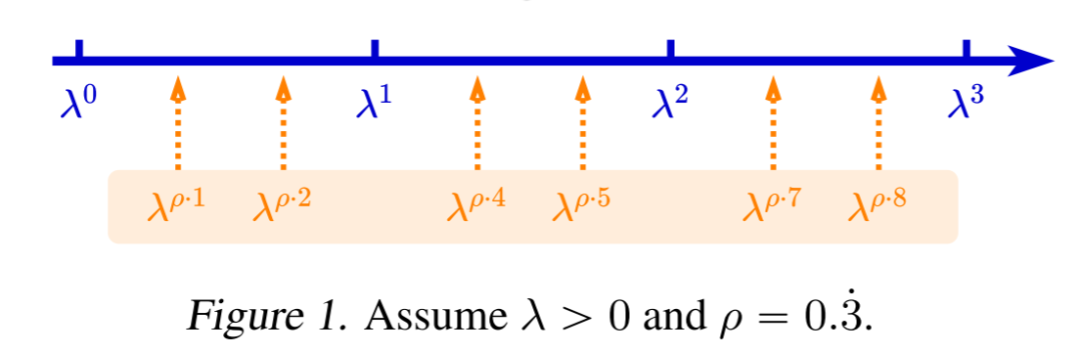
与一般谱方法不同， 不需要是有界谱。它可以利用更多的基，同时通过将控制在一个较小的范围内来缓解递减和发散问题。因此，如下图所示，可以被认为是一种基增强技术：

滤波器基上的广义归一化

直接对频谱进行运算，可以实现对频谱范围的精确控制，但需要进行特征分解。为了避免特征分解，本文还研究了图归一化对谱的影响，将归一化邻接矩阵推广如下 ：

实验分析

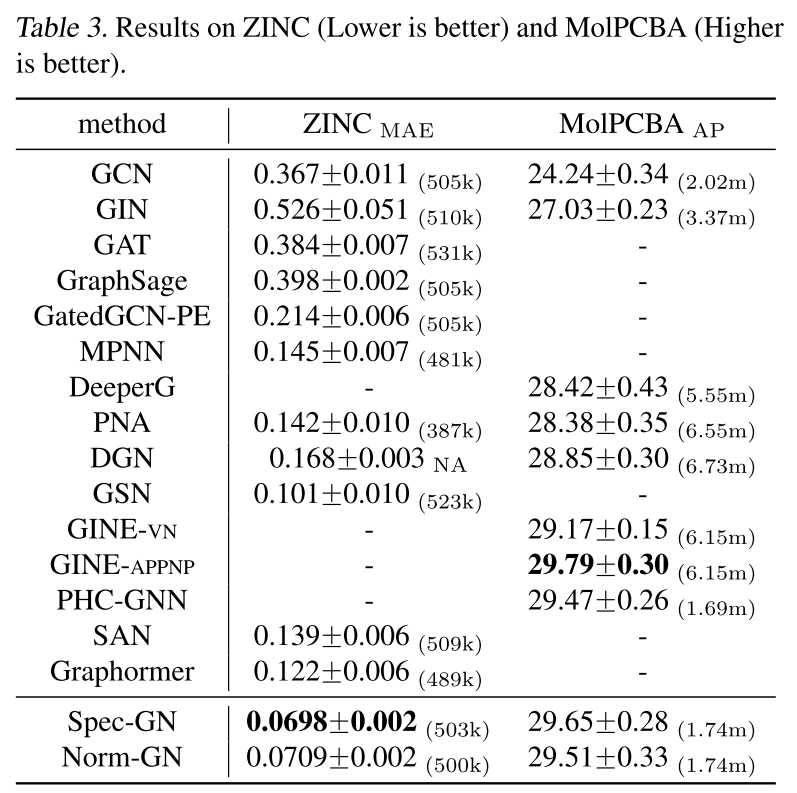
下表总结了本文的方法与TUDatasets、ZINC和MolPCBA基线的比较：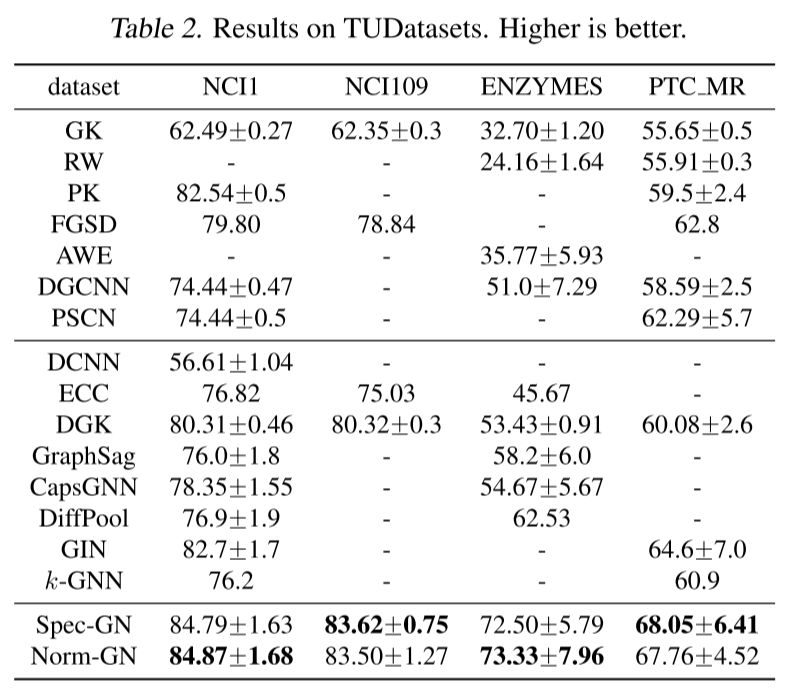

总结

本文研究了GNNS中光谱的影响。结果表明，在现有的结构中，不光滑的频谱会导致相关性问题，这是开发深层模型和应用更强大的图滤波器的障碍。在此基础上，本文提出了无相关结构，将相关问题与滤波器设计解耦。然后本文证明了谱特性也阻碍了多项式滤波器的逼近能力，并通过改变图的谱来解决这一问题。本文的大量实验表明，具有强大滤波器的无相关结构具有显著的性能增益。