ICML 2022 | Nonlinear Feature Diffusion on Hypergraphs
“文章信息
来源:Proceedings of the 39th International Conference on Machine Learning(ICML) 2022
”
标题:Nonlinear Feature Diffusion on Hypergraphs
作者:Konstantin Prokopchik, Austin R Benson, Francesco Tudisco
链接:https://proceedings.mlr.press/v162/prokopchik22a.html
代码:https://github.com/compile-gssi-lab/HyperND
内容简介
超图是数据中多向关系的常见模型,超图半监督学习是在给定标签的几个节点上为超图中的所有节点分配标签的问题。扩散和标签传播是图设置中半监督学习的经典技术,并且有一些标准方法可以将它们扩展到超图。然而这些方法是线性模型,并没有提供一种明显的方式来结合节点特征进行预测。本文在超图上开发了一个非线性扩散过程,它按照超图结构传播特征和标签。尽管该过程是非线性的,但本文展示了对于广泛的非线性类别的全局收敛到一个独特的限制点,并且证明了这种限制是一种新的正则化半监督学习损失函数的全局最小值,该损失函数旨在减少广义形式的跨超边的节点特征的方差。限制点作为一个节点嵌入,本文从中使用线性模型进行预测。本文的方法与流行的图和超图神经网络基线具有竞争力,而且训练时间也更少。
本文的主要贡献如下:
本文将 GNN 的思想和超图上 SSL 的扩散与一种根据超图结构同时扩散标签和特征的方法相结合。除了结合特征之外,新的扩散方法还可以结合广泛的非线性来提高建模能力,这对于图和超图神经网络的架构都至关重要。该过程的限制点在每个节点处提供嵌入,然后可以将其与更简单的模型(例如多项逻辑回归)结合以在每个节点处进行预测。这导致了一种比典型 GNN 快得多的方法,因为训练阶段和嵌入计算是解耦的。 即使模型是非线性的,本文仍然可以证明一些关于扩散过程的理论性质。特别是本文证明了该过程的限制点是唯一的,并提供了一种简单的、全局收敛的迭代算法来计算它。此外,本文表明这个限制点是可解释的超图 SSL 损失函数的全局最优值,该损失函数定义为数据拟合项和类似拉普拉斯的正则化器的组合,旨在减少每个超边上的“广义方差”形式。 实验表明,使用本文的非线性超图扩散的极限点作为线性模型的特征,在几个真实世界的数据集上与各种图和超图神经网络基线以及其他扩散算法具有竞争力。该研究还通过删除或修改节点特征来研究输入特征嵌入对分类性能的影响。将超图 GNN 的最终嵌入作为扩散模型中的附加特征并不能提高准确性,这证明本文的模型对于经验数据是足够的。
相关工作
本文回顾了用于 SSL 和超图标签传播 (HLS) 的超图神经网络 (HNN) 的基本思想,把接下来开发的方法背景化。
神经网络方法
图神经网络是广泛采用的图半监督学习方法。已经提出了对超图的几种概括,本文总结了最基本的想法。当 对于所有,超图是标准图 。图卷积网络 (GCN) 的基本公式 (Kipf & Welling, 2017) 是基于图信号上卷积算子的一阶近似 (Mallat, 1999)。这种近似归结为图的归一化邻接矩阵给出的映射,其中 是(可能重新缩放的)归一化拉普拉斯算子,A 是邻接矩阵。两层 GCN 的前向模型是
拉普拉斯正则化和标签传播
基于类拉普拉斯正则化策略的半监督学习在 (Zhou et al., 2004) 中开发用于图,然后在 (Zhou et al., 2007) 用于超图。这些方法的主要思想是通过最小化正则化平方损失函数来获得分类器
其中是考虑超图结构的正则化项。(请注意,这里只使用标签,而不是特征。)特别是如果 ,: 表示 的第行,则图扩展方法定义 ,和
超边方差正则化和非线性扩散
本文提出了一个新的超图正则化项,它不是最小化超边上每个节点对之间的距离,而是旨在减少超边节点之间的方差(或广义方差),准确地说,考虑形式的正则化项
非线性扩散法
考虑正则化损失函数,一般是非二次且非凸的。尽管如此,本文展示的全局解可以通过类似于 HLS 的非线性版本的简单超图扩散算法来计算,前提是将嵌入集限制为非负条目。
每个节点都有一个标签编码向量 (是初始未标记点 的全零向量)和一个特征向量 。因此,超图中的每个节点都有一个初始的 维嵌入,它形成了一个输入矩阵。本文所提出的超图半监督分类器使用非线性扩散过程的归一化极限点如下:
相关算法描述如下:
相关的非线性扩散模型
本文的非线性扩散过程通过超图传播输入节点标签和特征嵌入,但允许非线性激活,这增加了建模能力。首先,是扩展超图的归一化邻接矩阵的推广。其次,对于标准图,即所有边恰好有两个节点的超图,其中是图的邻接矩阵,是加权节点度的对角矩阵。类似地,对于一般超图 ,有恒等式 ,其中 是与 关联的扩展图邻接矩阵。那么,L可以表示为:
模型扩展到任意大小的超边的情况需要将超边分成相同大小的批次并计算相应的邻接张量。与本文提出的关联矩阵模型相比,这在计算上的要求要高得多,因为它需要计算几个高阶张量,而且张量的乘法运算比矩阵的乘法运算更昂贵(使用来自例如 NumPy 的快速 BLAS 例程) ,尤其是在用于传播高维特征而不仅仅是标签时。
实验分析
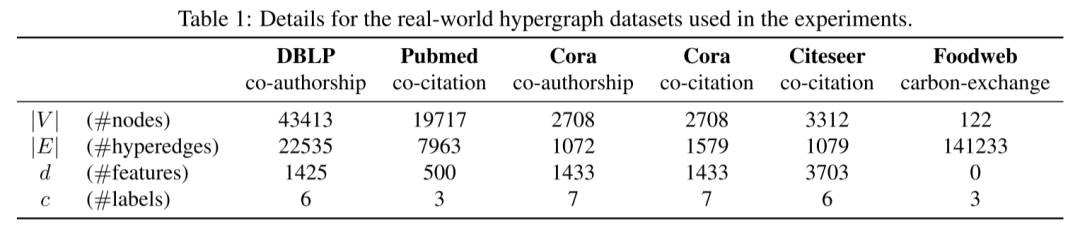
本文在几个真实世界的超图数据集上评估提出的方法,如下表所示:
本文使用五个共同被引和共同作者超图:Cora co-authorship、Cora cocitation、Citeseer、Pubmed (Sen et al., 2008) 和 DBLP (Rossi & Ahmed, 2015)。数据集中的所有节点都是文档,特征由摘要的内容给出,超边连接基于共同引用或共同作者。每个数据集的任务是预测文档所属的主题。本文还考虑了一个食物网超图,其中节点是生物体,超边表示佛罗里达湾中的定向碳交换,预测节点在食物链中的作用。这个超图没有特征,所以 HyperND 只使用标签,而对基线使用 onehot 编码。
实验结果如下图:

总结
图神经网络和超图标签扩展是两种不同的技术,对于具有高阶关系数据的半监督学习具有不同的优势。本文提出的扩散方法 (HyperND) 试图结合两种方法的优点:基于特征的学习、建模灵活性、基于标签的正则化和计算速度。重要的是,本文可以证明扩散收敛到嵌入,它是可解释的正则化损失函数的全局最小化,它在超边上强制执行小方差,并且有特定算法可以计算这个最佳嵌入。总体而言,HyperND 在多个数据集上优于各种基线神经网络和基于标签传播的方法。