一、任务
前面在《递归学习笔记(三)——几种递归方法的时间效率》一文中测试了尾递归函数的递归深度,发现跟普通的递归函数差不多,都是3000多一点。由于迄今为止的Python解释器并没有对尾递归进行优化,导致尾递归的空间效率没有充分发挥出来。
在Python当中对尾递归进行优化的方法还是有的,就是利用装饰器。小编对装饰器一点不懂,就抄一下作业,给出一个优化尾递归的例子。
二、环境
Win7中文旗舰版64位 + Python 3.64 64位
三、什么是尾递归
尾递归也不是太了解,直接给出百度词条上的解释:
如果一个函数中所有递归形式的调用都出现在函数的末尾,我们称这个递归函数是尾递归的。当递归调用是整个函数体中最后执行的语句且它的返回值不属于表达式的一部分时,这个递归调用就是尾递归。尾递归函数的特点是在回归过程中不用做任何操作,这个特性很重要,因为大多数现代的编译器会利用这种特点自动生成优化的代码。
我们通常写的递归程序,一般不是尾递归,例如,《递归学习笔记(三)——几种递归方法的时间效率》给出的函数p3所调用的递归函数p3sub,该函数是这么定义的:
def p3sub(a, n):
if n == 0:
return 1
else:
return a * p3sub(a, n-1)
尽管这个递归调用出现在了函数的末尾,但它不是尾递归,因为它的返回值是
a * p3sub(a, n-1)
它的递归调用属于表达式的一部分,这不算尾递归。
相比之下,p4sub就是一个尾递归函数:
def p4sub(a, t, n):
if n == 0:
return t
else:
return p4sub(a, t*a, n-1)
如何把普通递归转成尾递归,小编目前还不是太了解,但感觉从p3sub变到p4sub,递归函数多了一个参数,刚好用来逐步存储普通递归函数中的返回值是一个表达式,这个变量就是在递归终结时用来存储返回最终结果的。奔着这样的一个猜测,我们可以把一个求阶乘的普通递归函数跟改为尾递归函数。
求阶乘的普通递归函数:
def j(n):
if n<=1:
return 1
else:
return n * j(n-1)
求阶乘的尾递归函数:
def j2sub(t, n):
if n<=1:
return t
else:
return j2sub(t*n, n-1)
def j2(n):
return j2sub(1, n)
四、用装饰器来优化尾递归
这一部分是抄作业,感谢鸾林居士在CSDN上给出的一段优化尾递归的装饰器代码。这段代码的下载地址是:
https://blog.csdn.net/abc_12366/article/details/79798296
代码非常好用,一字不易抄在这里,当然,这段代码的版权属于鸾林居士所有:
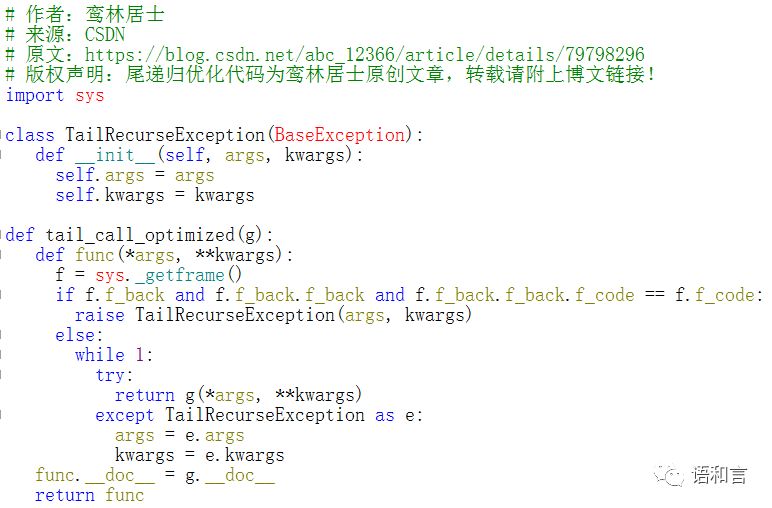
装饰器的用法:
在定义尾递归函数之前加上如下的一句:
@tail_call_optimized
其它一切照常写就行。下面给出完整的代码:
五、用装饰器优化尾递归的完整代码

六、测试结果
上面的代码,递归深度达到一亿也没问题,如果代码中不写 @tail_call_optimized 这个语句,递归调用900多次就崩溃了。这说明尾递归优化代码起作用了。不过运行到后来,速度会非常慢。






