1 前言
1.1 场(field)
在物理里,场是一个以时空为变数的物理量。空间中弥漫着的基本相互作用被命名为“场”。场可以分为标量场(scalar field)、向量场(vector field)和张量场(tensor field)等,依据场在时空中每一点的值是标量、向量还是张量而定。更进一步地,在每一范畴(标量、向量、张量)之中,场还可以分为“经典场”和“量子场”两种,依据场的值是数字或量子算符而定。
1.2 四元数
四元数(quaternion)是由爱尔兰数学家威廉·卢云·哈密顿(Hamilton)1843年创立出的数学概念,通常记为H或。如把四元数的集合考虑成多维实数空间的话,四元数则代表着一个四维空间,相对于复数为二维空间。四元数以a+bi+cj+dk的形式说明空间点所在位置,i、j、k作为一种特殊的虚数单位参与运算,并有以下运算规则:
四元数是复数的不可交换延伸。
一个四元数h=a+bi+cj+dk的共轭值定义为,其模为:
四元数的乘逆为:
四元数的矩阵表示:
泡利矩阵:
四元数矩阵:
任意的四元数可以表示为:
1.3 从四元数到算符
单位向量规则 
Hamilton引进符号(称其为"nabla")来代表向量微分算符(differential vector operators),在笛卡儿坐标中:
设,在四元数运算里:
数学家一时曾对四元数感兴趣,但物理、化学家却不然,上式由一个标量部分和一个三维向量构成,把标量部分(我们称之为f的散度)和向量部分(我们称为f的旋度)分开,分别应用不同的ijk规则,可以得到一些更有用的东西,看出这一点的正是Gibbs。于是,散度(divergence)定义为和向量函数的点积,旋度(curl)定义为和向量函数的叉积:
需要再次强调,ijk规则对于四元数和对于向量是不同的,而向量中对于点积和叉积又是不同的。
2 向量微分算符
2.1 梯度(gradient)
对标量函数的运算产生f的梯度(向量),设f=f(x,y,z),
2.1.1 方向导数
为考察梯度的物理意义,先回顾一下方向导数的概念。如下图,设函数f(x,y,z)在某一空间内有定义并且可微,令为一个使f(P)等于某个常数k的曲面或点的集合,令为另一个曲面,非常靠近,它使f(P') = k + Δk,则位于点A 的、方向是从A到A'的直线的方向导数为:
与在上取哪一点无关,但导数却与之有关。B是上最接近A的点,当|Δs|极小时,导数将有极大值,即Δs与AB(Δn)重合。若n是从A 指向B的单位长度向量,则n(df(P)/dn) 表示f(P)在大小和方向上的最大空间增加速率,是一个向量,我们称这个向量为f(x,y,z)在A点的梯度。 令为方向上的单位向量,则可以将该方向导数表示成:
当θ=0时,方向导数取到最大值,对应的是df(P)/ds变成df(P)/dn,其大小正是梯度的大小:
位于任何一点的梯度是一个向量,其大小是方向导数在该点可以取到的最大值,在梯度的方向上函数值变化最快。
2.1.2 一些例子
在我们熟悉的情况下:
考虑对的作用():
令r方向的单位向量为,则:
在库伦定律中,电势与1/r成正比,可以推出库仑力与距离的平方成正比
对于一般径向势的情形,,
与直觉一致,增加最快的方向是径向方向,其大小为。
2.2 散度(divergence)
2.2.1 连续性方程、管形场
通过考虑任何量(热、电荷、物质等等)通过一个体积元的流,可以看出散度的物理意义。
考虑一个体积元,其一角位于,令J为流过垂直于J的平面的单位面积流速。J沿x轴的分量如下图所示,在x方向上流进面上的流速为,在流出面的流速为,净流出为:
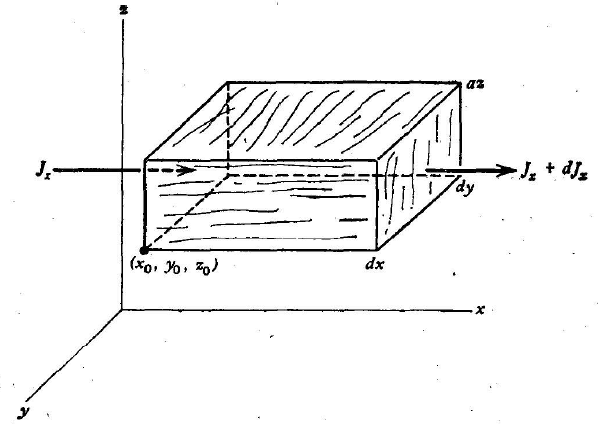
在y、z方向上用同样的方法,得到:
可见向量J的散度是单位体积的净流出体积流速。 若所考虑的物质的密度(不是流密度)是,则单位体积的物质损失速率也可以表示成,此时(v为速度),因此得到恒等式: 上式称为连续性方程,数学上表达了守恒(能量、电荷、物质等)定律。一个不可压缩流体流进和流出某一体积元的速率必相等,这样的流场的散度是零,就说它是管形的(solenoidal),相应的场为管形场/螺线向量场。
若J代表电流密度,即单位时间内流过单位曲面的电荷流,ρ代表某区域内的电荷密度,若电荷流是稳定的,电流密度不变(),则电荷守恒:
2.2.2 一些例子
坐标向量的散度
中心力场散度
利用:
得到:
当时:
2.3 旋度(curl)
2.3.1 无旋向量场
给定向量场B,考虑闭合路径线积分,分为1、2、3、4四段(z=0): 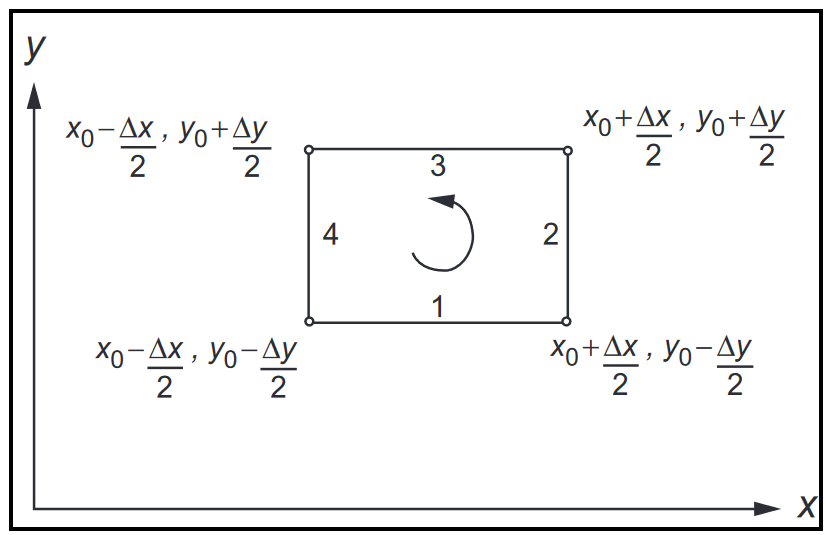
如果非零,对应着的非零组分,在小的环路内,线积分与环路面积成正比,单位区域的线积分值称为循环(circulation)(在流体力学中称为涡度(vorticity))。 我们将旋度为零的向量称为无旋(irrotational)的,相应的向量场为无旋向量场。
2.3.2 一些例子
中心力场的旋度(,其中):
可见中心力场的旋度为0。对于中心力场,力线(the lines of force)是辐射状的,无法形成闭环,相应的,我们发现旋度为零。
非零旋度
考虑,设,则,则:
在该例中,的流线(stream lines)是关于原点的逆时针圆,对应的旋度非零。
3 算符的复合
3.1 一些公式
若f和g是标量函数,A、B、C是向量函数,则下列各式成立:
3.2 的复合
当算符对某一个标量作用两次()时,就得到了Laplace算符(Laplacian):
Laplace 算符也可以对向量函数运算,但不像对标量函数的运算那样常见。
,假设一阶偏微分顺序可交换(即的二阶导数是连续的)
当我们写成行列式来记忆旋度运算时,是自上而下相乘的,因此将移到行列式外面是合理的。
从上式可以看出,梯度的旋度为零,梯度是无旋的。
,假设V具有足够的连续性。
从上式可以看出,旋度的散度为零,旋度是管形的。
向量拉普拉斯算符
先推导一下向量的三重积(Vector Triple Product)公式:
推导过程如下:
为列维-奇维塔符号(Levi-Civita symbol)(取值为+1、-1、0,顺序为+1,任意角标交换一次变号)
下面考虑
式中称为向量拉普拉斯算符(vector Laplacian),有时写为,在笛卡尔坐标系(直角坐标系和斜坐标系的统称),是向量,其第i个组分为。尽管公式是一般的,但分解为拉普拉斯算子作用于V的各个组分()只有在笛卡尔坐标系下才成立。
[1](美)登斯(J.B.DENCE). 化学中的数学方法[M]. 王知群.科学出版社, 1981.
[2] ARFKEN G B, WEBER H J, HARRIS F E. Mathematical Methods for Physicists: A Comprehensive Guide[M]. 7th edition. Amsterdam ; Boston: Academic Press, 2012.
[3] wikipedia






