背景介绍和问题定义
子图匹配(subgraph matching)是图数据管理中一个重要的问题,在社交网络、化学分子分析等领域也有其应用。
给定一个查询图Q和数据图G,子图匹配的目标是找到所有从查询图到数据图的子图同构。一个子图同构是从查询图到数据图的单射,保持查询图点和边的标签。也有些子图匹配任务目标是寻找子图同态。相比子图同构,子图同态取消了映射为单射的限制,可以让多个查询图中节点映射到同一个数据图中的点。
我们常用的图数据管理系统gStore的查询本质上是找到所有子图同态。如果想要在gStore在子图同构的意义下进行子图匹配,可以利用“filter”语句,如“filter ?v1 != ?v2”可以限制变量?v1和?v2的映射像不同。
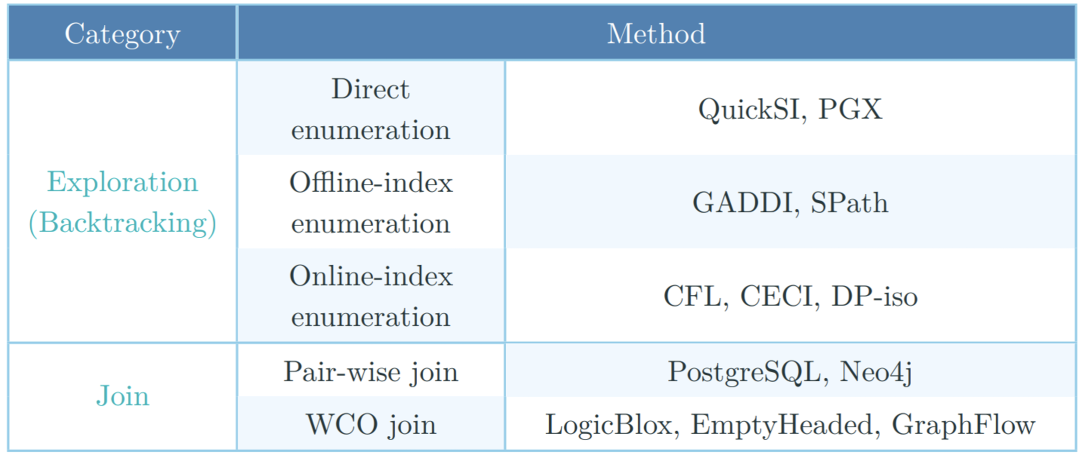
现有的子图匹配方法可以分为基于探索(exploration)(本质是回溯(backtracking)算法)和基于连接(join)两大类方法[1]。其中基于探索的方法又可根据是否使用索引和使用何种索引进一步分类为直接枚举、offline-index枚举、online-index枚举三类方法。基于连接的方法又可进一步分为两两连接和WCO连接的方法。详见下图:接下来我们会介绍上面分类中除了两两连接以外的方法的基本思想和代表作。直接枚举方法
一般而言,子图匹配算法主要有三大步骤:过滤候选集、生成变量搜索(或者连接)次序、根据候选集和搜索(连接)次序枚举。不同的方法会有不同方式进行这三大步骤。而直接枚举方法一般可以作为baseline。在过滤候选集阶段,会根据查询图的某些条件和特征,对每个变量Vi节点生成一个C(Vi)数据图中节点的集合,作为候选集。后续枚举会从这个候选集开始,避免了枚举数据图中没有匹配希望的节点引起的多余计算。常见的过滤方法包括根据标签(label)过滤、根据度数(degree)过滤等。在生成变量搜索次序阶段,会根据数据库的采样集合或者根据一些代价估计,生成一个查询图变量的次序 ,一般要求
,一般要求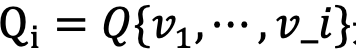 是联通的查询图。在第三阶段,会根据搜索次序,遍历变量的候选集,如果能形成一个匹配,则输出该匹配,否则考虑下一个可能的匹配。很容易发现,上面的直接枚举方法的复杂度为
是联通的查询图。在第三阶段,会根据搜索次序,遍历变量的候选集,如果能形成一个匹配,则输出该匹配,否则考虑下一个可能的匹配。很容易发现,上面的直接枚举方法的复杂度为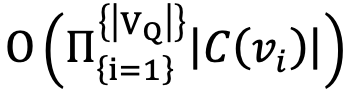 ,后续各种改进都试图通过各种技巧降低该复杂度。一个可能的方向是在直接枚举方法中引入并行处理技术,例如Oracle的PGX.ISO方法[2]。其并行技术中主要有两大改进:(a) 将一般的直接枚举方法中的枚举模式从DFS枚举改为BFS枚举模式,这个改进更加适合PGX.ISO的中间结果的存储和并行执行的进行。需要注意的是BFS可能会带来更大的内存开销,但由于PGX.ISO引入并行,内存开销也是可以接受的。(b)在枚举每一步的末尾,将各个工作线程的结果收集到一个总线程存储下来,收集完毕后,再平均分配给各个工作线程进行下一步枚举。
,后续各种改进都试图通过各种技巧降低该复杂度。一个可能的方向是在直接枚举方法中引入并行处理技术,例如Oracle的PGX.ISO方法[2]。其并行技术中主要有两大改进:(a) 将一般的直接枚举方法中的枚举模式从DFS枚举改为BFS枚举模式,这个改进更加适合PGX.ISO的中间结果的存储和并行执行的进行。需要注意的是BFS可能会带来更大的内存开销,但由于PGX.ISO引入并行,内存开销也是可以接受的。(b)在枚举每一步的末尾,将各个工作线程的结果收集到一个总线程存储下来,收集完毕后,再平均分配给各个工作线程进行下一步枚举。Offline-index枚举方法
Offline-index枚举方法通过预先处理数据库,一般是存储一些特殊图模式匹配的数目或具体匹配,从而便于实际执行查询时过滤查询变量的候选集:如果查询图某点附近的邻域内有某个模式,那么数据图中其匹配点的附近邻域也必有这个模式的匹配;否则数据图中的这个点不能匹配该查询点。下面介绍两个offline-index枚举方法的工作:GADDI和SPath。GADDI[3]预先扫描整个数据图,挖掘一些特殊的图模式。接着对于图中距离比较近的所有点对(u,v),计算u和v的k步邻域交集中那些图模式的匹配数目存储下来(这个值在原文中被称为neighboring discriminating substructure distance, NDS distance)。在查询执行的枚举过程中,如果数据图中的点与附近点的NDS距离比查询图中对应点对间的NDS距离小,则可以判定为不能匹配上,从而可从候选集中去除这个数据点。SPath[4]与一般方法不同,其主要思想为一次匹配一个路径(path),然后再对路径匹配的结果做连接,这样既减小了直接枚举方法复杂度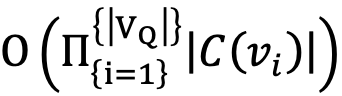 中的
中的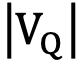 ,也减小了每个候选集的大小。其具体做法是,对数据图中的每个点u,存储数据图中与u最短距离恰好为k的那些点v,并根据的标签,分类存储好。通过这种离线索引,可以容易得找到查询图中一条路径的匹配,具体步骤限于篇幅在此不做展开,感兴趣的同学可以参考原文。
,也减小了每个候选集的大小。其具体做法是,对数据图中的每个点u,存储数据图中与u最短距离恰好为k的那些点v,并根据的标签,分类存储好。通过这种离线索引,可以容易得找到查询图中一条路径的匹配,具体步骤限于篇幅在此不做展开,感兴趣的同学可以参考原文。Online-index枚举方法
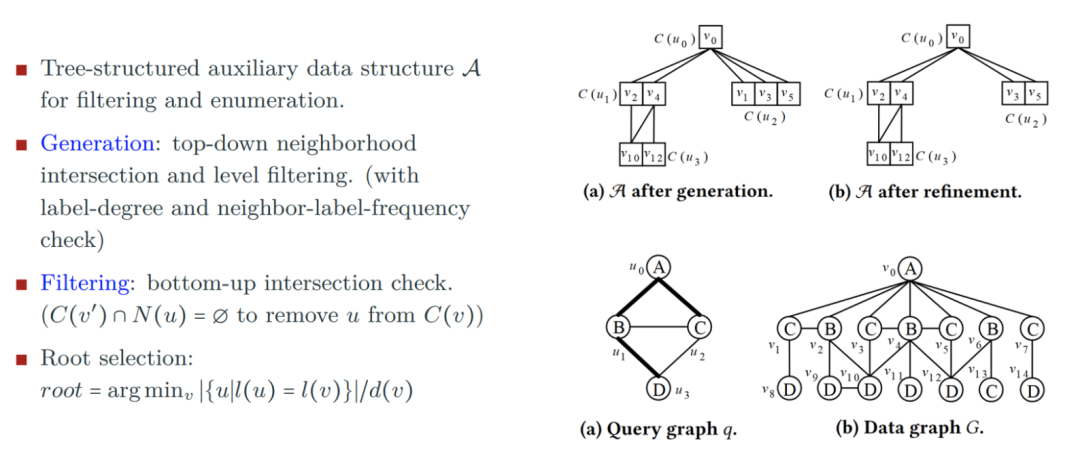
由于offline-index枚举方法需要预先处理数据,且构建索引时间较长,后续的基于索引的方法一般都是online的,即在查询过程中,构建索引结构帮助过滤候选集。由于上周公众号论文导读介绍过很多online-index枚举方法中,本文就仅介绍一个代表工作CFL,以此来说明offline-index枚举和online-index枚举的主要区别。CFL[5]方法中,在第一步生成候选集时,构建一个树形数据结构。具体做法为:首先根据代价模型选择查询图中一个点作为树的根节点,并抽取出树边,剩余边作为非树边。接着根据从根到叶子的从上至下和同层树节点连边生成每个查询点的候选集,并连接上下两层候选集点代表数据图中的边。最后再从底至上根据儿子过滤父亲节点的候选集。下图用一个例子说明了这个步骤。WCO Join方法
最坏情况最优连接(worst-case-optimal join)是近年来一种新的连接理念,其目标是在给定数据库元组数目的情况下,寻求一种通用的连接算法,使得最坏情况下(连接结果数最大),算法也能保证很好的性能。要深入理解这种连接算法,同学们可以去了解AGM bound、分数边覆盖等概念并阅读相关论文[6]。LogicBlox[7]是一个应用WCO join方法执行查询的系统。LogicBlox中应用的连接算法名为跳蛙算法(leapfrog triejoin),其包含单变量求交和多变量连接两块技巧。在单变量求交中,假设我们需要求一些集合元素的交集,我们预先将各个集合排序,再根据最小值的大小排成一列。如下图中A、B、C的顺序,我们发现集合A的最小元素与集合C的最小元素2不相等,我们便在A中寻找大于等于2的最小元素。依次做下去,知道迭代器位置的元素都是相同的,例如图中的元素8位置,则代表找到了一个交集中的元素,输出即可,再继续之前的步骤直到所有集合完成遍历。画出这个过程,便可直观地理解“跳蛙”之名的意义。在多变量连接中,LogicBlox也需要一个查询变量的连接次序,不同边代表关系存成Trie树,一层代表了一个变量,同层之间做上面介绍的单变量求交步骤,便可得到连接结果。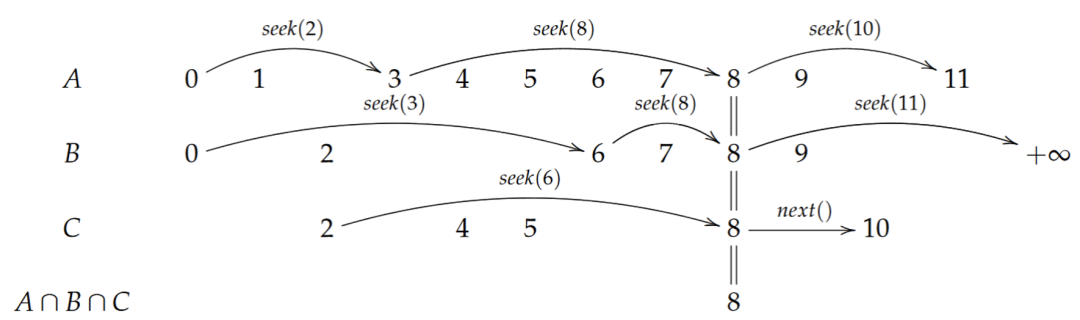
最近也还有其他一些应用WCO连接算法到图数据库查询中,例如EmptyHeaded[8]和GraphFlow[9]。当然,在最新的gStore图数据库系统[10]中,我们除了使用WCO连接算法,也考虑了二元连接优化。通过我们的优化器,我们可以生成包含WCO连接算法和二元连接的执行计划,从而加速查询。总结
通过研究这些子图匹配算法和系统,我们总结几点发现和可能的研究方向:1. 基于索引的方法中索引的作用主要是过滤候选集。Offline-index枚举方法通常需要大量预处理时间;而online-index枚举方法无需预先处理,且能在过滤候选集和枚举步骤中取得不错的性能。2. 基于探索的回溯算法与DFS枚举模式下的WCO连接算法本质上是一样的。而WCO连接算法在BFS枚举模式下非常适合并行。3. 有三个可能的研究方向:(a)更好的过滤候选集策略;(b)更优的变量探索(连接)次序;(c)在执行过程中引入并行。参考文献
[1] Shixuan Sun and Qiong Luo. In-memory subgraph matching: An in-depth study. In Proceedings of the2020 ACM SIGMOD International Conference on Management of Data, pages 1083–1098, 2020.[2] Raghavan Raman, Oskar van Rest, Sungpack Hong, Zhe Wu, Hassan Chafi, and Jay Banerjee. Pgx.iso: Parallel and efficient in-memory engine for subgraph isomorphism. In Proceedings of Workshop on GRAph Data Management Experiences and Systems, GRADES’14, page 1–6, New York, NY, USA, 2014. Association for Computing Machinery.[3] Shijie Zhang, Shirong Li, and Jiong Yang. Gaddi: Distance index based subgraph matching in biological networks. In Proceedings of the 12th International Conference on Extending Database Technology: Advances in Database Technology, EDBT ’09, page 192–203, New York, NY, USA, 2009. Association for Computing Machinery.[4] Peixiang Zhao and Jiawei Han. On graph query optimization in large networks. Proc. VLDB Endow., 3(1–2):340–351, sep 2010.[5] Fei Bi, Lijun Chang, Xuemin Lin, Lu Qin, and Wenjie Zhang. Efficient subgraph matching by postponing cartesian products. In Proceedings of the 2016 International Conference on Management of Data, SIGMOD ’16, page 1199–1214, New York, NY, USA, 2016. Association for Computing Machinery.[6] Hung Q. Ngo, Ely Porat, Christopher Ré, and Atri Rudra. Worst-case optimal join algorithms. J. ACM, 65(3), mar 2018.[7] Molham Aref, Balder ten Cate, Todd J. Green, Benny Kimelfeld, Dan Olteanu, Emir Pasalic, Todd L. Veldhuizen, and Geoffrey Washburn. Design and implementation of the logicblox system. In Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data, SIGMOD ’15, page 1371–1382, New York, NY, USA, 2015. Association for Computing Machinery.[8] Christopher R. Aberger, Susan Tu, Kunle Olukotun, and Christopher Ré. Emptyheaded: A relational engine for graph processing. In Proceedings of the 2016 International Conference on Management of Data, SIGMOD ’16, page 431–446, New York, NY, USA, 2016. Association for Computing Machinery.[9] Chathura Kankanamge, Siddhartha Sahu, Amine Mhedbhi, Jeremy Chen, and Semih Salihoglu. Graphflow: An active graph database. In Proceedings of the 2017 ACM International Conference on Management of Data, SIGMOD ’17, page 1695–1698, New York, NY, USA, 2017. Association for Computing Machinery.[10] Linglin Yang, Lei Yang, Yue Pang, and Lei Zou. gCBO: A cost-based optimizer for graph databases. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, pages 5054–5058, 2022.
欢迎关注北京大学王选计算机研究所数据管理实验室微信公众号“图谱学苑“
实验室官网:https://mod.wict.pku.edu.cn/
微信社区群:请回复“社区”获取
实验室开源产品图数据库gStore:
gStore官网:http://www.gstore.cn/
GitHub:https://github.com/pkumod/gStore
Gitee:https://gitee.com/PKUMOD/gStore
 ,一般要求
,一般要求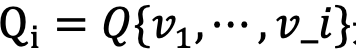 是联通的查询图。
是联通的查询图。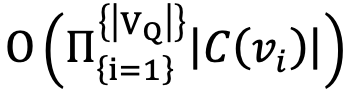 ,后续各种改进都试图通过各种技巧降低该复杂度。
,后续各种改进都试图通过各种技巧降低该复杂度。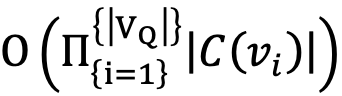 中的
中的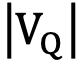 ,也减小了每个候选集的大小。其具体做法是,对数据图中的每个点u,存储数据图中与u最短距离恰好为k的那些点v,并根据的标签,分类存储好。通过这种离线索引,可以容易得找到查询图中一条路径的匹配,具体步骤限于篇幅在此不做展开,感兴趣的同学可以参考原文。
,也减小了每个候选集的大小。其具体做法是,对数据图中的每个点u,存储数据图中与u最短距离恰好为k的那些点v,并根据的标签,分类存储好。通过这种离线索引,可以容易得找到查询图中一条路径的匹配,具体步骤限于篇幅在此不做展开,感兴趣的同学可以参考原文。