一、说明
我们先来看一组例子
【PYTHON】
Python 3.6.10 (default, Apr 6 2021, 21:58:27)
[GCC 4.8.5 20150623 (Red Hat 4.8.5-44)] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>>
>>> round(1.45,1)
1.4
>>> round(1.55,1)
1.6
【JAVA】
public static void main(String[] args) {
System.out.println(1.45f + " --> " + String.format("%.1f", 1.45f));
System.out.println(1.55f + " --> " + String.format("%.1f", 1.55f));
}
结果:
1.45 --> 1.5
1.55 --> 1.5
大家看出问题来了吗,在python和java中四舍五入的结果跟我们想的不一样,而且python和java的四舍五入规则还不一样,这是为什么?
| 实际值 | 1.45 | 1.55 |
|---|---|---|
| python round | 1.4 | 1.6 |
| java round | 1.5 | 1.5 |
二、猜想
针对上面的现象,肯定不能说编程语言有bug,那么编程语言为什么会出现这样的结果呢,我猜想原因可能是这样的。在计算机中,所有数据的存储全是0和1,这是常识。对于数字也不例外,整数的存储很好理解,就是二进制,比如1001,就代表9。对于小数的存储,一般用浮点数表示,浮点数的整数部分可以用二进制精确表示,但是小数部分,却无法用二进制精确表示,只能是一个无限接近的值。对于上面round的结果跟我们预想的不一样会不会是由于浮点数特有的误差引起的呢?比如1.45在计算机中可能存的是1.44999999,也可能存的是1.45000001。前者round保留一位小数的确就是1.4,而后者却是1.5。
三、验证
为了验证上面的猜想,我们先用java看看一组数四舍五入后的结果。
public static void main(String[] args) {
float f[] = {1.05f, 1.15f, 1.25f, 1.35f, 1.45f, 1.55f, 1.65f, 1.75f, 1.85f, 1.95f};
for (float v : f) {
String result = String.format("%.1f", v);
System.out.println(v + " --> " + result);
}
}
结果:
1.05 --> 1.0 不正确
1.15 --> 1.1 不正确
1.25 --> 1.3
1.35 --> 1.4
1.45 --> 1.5
1.55 --> 1.5 不正确
1.65 --> 1.6 不正确
1.75 --> 1.8
1.85 --> 1.9
1.95 --> 2.0
现在我们只需要知道这个小数在计算机中是怎么存储的,就可以验证我们的猜想了。如何将一个小数转换为浮点数算法比较复杂,为了节约篇幅,不在本文介绍。我们可以通过一个小工具进行转换。现行的浮点数算法采用的是IEEE 754,我们可以登录这个网页(https://www.h-schmidt.net/FloatConverter/IEEE754.html),利用上面提供的工具将小数转换为浮点数,看看我们所输入的值实际在计算机中存储的是什么样子。在工具里填入一个实际的值,下面的结果自动生成。

输入值 --> 计算机实际存储的值
1.05 --> 1.0499999523162841796875
1.15 --> 1.14999997615814208984375
1.25 --> 1.25
1.35 --> 1.35000002384185791015625
1.45 --> 1.4500000476837158203125
1.55 --> 1.5499999523162841796875
1.65 --> 1.64999997615814208984375
1.75 --> 1.75
1.85 --> 1.85000002384185791015625
1.95 --> 1.9500000476837158203125
可以看到正好跟java吻合。1.05存储的是1.0499999523162841796875,将这个数四舍五入保留一位小数不正好就是1.0么。
接下来看看python中的情况
>>> l = [1.05, 1.15, 1.25, 1.35, 1.45, 1.55, 1.65, 1.75, 1.85, 1.95]
>>> for v in l:
... print(v, '-->', round(v,1))
...
1.05 --> 1.1
1.15 --> 1.1 不正确
1.25 --> 1.2
1.35 --> 1.4
1.45 --> 1.4 不正确
1.55 --> 1.6
1.65 --> 1.6 不正确
1.75 --> 1.8
1.85 --> 1.9
1.95 --> 1.9 不正确
可以看到python跟java又不太一样,难道说python使用的是另一种算法?猛然想起,浮点数还分单精度和双精度,java的float是单精度,python的小数会不会是双精度呢?我们先看看双精度的浮点数如何表示。上面的工具只提供了单精度的转换,我们再另外找一个工具(https://www.binaryconvert.com/result_double.html?decimal=049046057053)。下面贴出来双精度的转换结果。
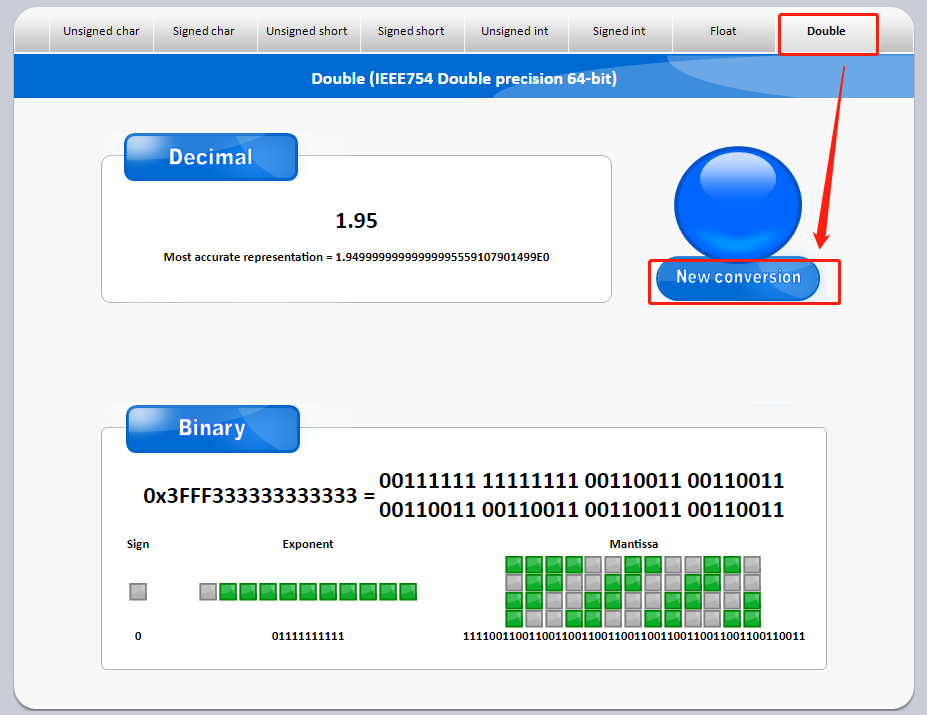
输入值 --> 计算机实际存储的值
1.05 --> 1.05000000000000004440892098501
1.15 --> 1.14999999999999991118215802999
1.25 --> 1.25
1.35 --> 1.35000000000000008881784197001
1.45 --> 1.44999999999999995559107901499
1.55 --> 1.55000000000000004440892098501
1.65 --> 1.64999999999999991118215802999
1.75 --> 1.75
1.85 --> 1.85000000000000008881784197001
1.95 --> 1.94999999999999995559107901499
可以看到双精度与python四舍五入的结果也正好吻合。
四、复核
到这里我其实很确信我的猜想是对的,但是为了进一步证明,我们还是要看官方的文档。
在python中我们可以通过以下代码,直接查看一个小数在计算机中存储的实际值,可以看到跟双精度浮点数完全一样。
>>> from decimal import Decimal
>>> l = [1.05, 1.15, 1.25, 1.35, 1.45, 1.55, 1.65, 1.75, 1.85, 1.95]
>>> for v in l:
... print(v, '-->', Decimal.from_float(v))
...
1.05 --> 1.0500000000000000444089209850062616169452667236328125
1.15 --> 1.149999999999999911182158029987476766109466552734375
1.25 --> 1.25
1.35 --> 1.350000000000000088817841970012523233890533447265625
1.45 --> 1.4499999999999999555910790149937383830547332763671875
1.55 --> 1.5500000000000000444089209850062616169452667236328125
1.65 --> 1.649999999999999911182158029987476766109466552734375
1.75 --> 1.75
1.85 --> 1.850000000000000088817841970012523233890533447265625
1.95 --> 1.9499999999999999555910790149937383830547332763671875
另外python的官方文档(https://python-reference.readthedocs.io/en/latest/docs/functions/round.html)里面也记录了一段话:“The behavior of round() for floats can be surprising: for example, round(2.675, 2) gives 2.67 instead of the expected 2.68. This is not a bug: it’s a result of the fact that most decimal fractions can’t be represented exactly as a float”。
五、联想
既然编程语言有这些现象,那么我们常用的数据库也有这个问题吗?因为我所处的行业是金融行业,对数据非常敏感,需要精确到分,即0.01,差一分也是问题。
1. 首先查看excel
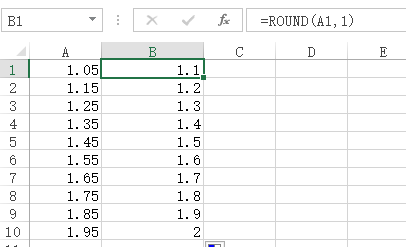
excel四舍五入正常
2. 其次查看oracle
SQL> create table t1 (id number, name varchar2(100));
SQL> insert into t1 values (1.05, '1.05');
SQL> insert into t1 values (1.15, '1.15');
SQL> insert into t1 values (1.25, '1.25');
SQL> insert into t1 values (1.35, '1.35');
SQL> insert into t1 values (1.45, '1.45');
SQL> insert into t1 values (1.55, '1.55');
SQL> insert into t1 values (1.65, '1.65');
SQL> insert into t1 values (1.75, '1.75');
SQL> insert into t1 values (1.85, '1.85');
SQL> insert into t1 values (1.95, '1.95');
SQL> commit;
SQL> select id, name, round(id, 1) from t1;
ID NAME ROUND(ID,1)
---------- ---------- -----------
1.05 1.05 1.1
1.15 1.15 1.2
1.25 1.25 1.3
1.35 1.35 1.4
1.45 1.45 1.5
1.55 1.55 1.6
1.65 1.65 1.7
1.75 1.75 1.8
1.85 1.85 1.9
1.95 1.95 2
oracle四舍五入正常
3. 再看mysql
mysql的小数有几种类型,float,double,decimal。float和double就是前面说的单精度和双精度浮点数,decimal是定点数,本文只讨论浮点数,因此定点数不做解释,只拿来做对比。
(root@localhost)[hello]> create table t2 (id1 float(10, 2), id2 decimal(10, 2), name varchar(100));
(root@localhost)[hello]> insert into t2 values (1.05, 1.05, '1.05');
(root@localhost)[hello]> insert into t2 values (1.15, 1.15, '1.15');
(root@localhost)[hello]> insert into t2 values (1.25, 1.25, '1.25');
(root@localhost)[hello]> insert into t2 values (1.35, 1.35, '1.35');
(root@localhost)[hello]> insert into t2 values (1.45, 1.45, '1.45');
(root@localhost)[hello]> insert into t2 values (1.55, 1.55, '1.55');
(root@localhost)[hello]> insert into t2 values (1.65, 1.65, '1.65');
(root@localhost)[hello]> insert into t2 values (1.75, 1.75, '1.75');
(root@localhost)[hello]> insert into t2 values (1.85, 1.85, '1.85');
(root@localhost)[hello]> insert into t2 values (1.95, 1.95, '1.95');
(root@localhost)[hello]> select id1, round(id1,1), id2, round(id2,1), name from t2;
+------+--------------+------+--------------+------+
| id1 | round(id1,1) | id2 | round(id2,1) | name |
+------+--------------+------+--------------+------+
| 1.05 | 1 | 1.05 | 1.1 | 1.05 |
| 1.15 | 1.1 | 1.15 | 1.2 | 1.15 |
| 1.25 | 1.2 | 1.25 | 1.3 | 1.25 |
| 1.35 | 1.4 | 1.35 | 1.4 | 1.35 |
| 1.45 | 1.5 | 1.45 | 1.5 | 1.45 |
| 1.55 | 1.5 | 1.55 | 1.6 | 1.55 |
| 1.65 | 1.6 | 1.65 | 1.7 | 1.65 |
| 1.75 | 1.8 | 1.75 | 1.8 | 1.75 |
| 1.85 | 1.9 | 1.85 | 1.9 | 1.85 |
| 1.95 | 2 | 1.95 | 2.0 | 1.95 |
+------+--------------+------+--------------+------+
可以看到mysql的浮点数四舍五入有问题,定点数四舍五入正常。
4. 最后看下sqlite
# ./sqlite3
SQLite version 3.36.0 2021-06-18 18:36:39
Enter ".help" for usage hints.
Connected to a transient in-memory database.
Use ".open FILENAME" to reopen on a persistent database.
sqlite>
sqlite> create table t3 (id1 real, id2 number(10,2), name varchar(100));
sqlite> insert into t3 values (1.05, 1.05, '1.05');
sqlite> insert into t3 values (1.15, 1.15, '1.15');
sqlite> insert into t3 values (1.25, 1.25, '1.25');
sqlite> insert into t3 values (1.35, 1.35, '1.35');
sqlite> insert into t3 values (1.45, 1.45, '1.45');
sqlite> insert into t3 values (1.55, 1.55, '1.55');
sqlite> insert into t3 values (1.65, 1.65, '1.65');
sqlite> insert into t3 values (1.75, 1.75, '1.75');
sqlite> insert into t3 values (1.85, 1.85, '1.85');
sqlite> insert into t3 values (1.95, 1.95, '1.95');
sqlite>
sqlite> select id1, round(id1,1), id2, round(id2,1), name from t3;
1.05|1.1|1.05|1.1|1.05
1.15|1.2|1.15|1.2|1.15
1.25|1.3|1.25|1.3|1.25
1.35|1.4|1.35|1.4|1.35
1.45|1.5|1.45|1.5|1.45
1.55|1.6|1.55|1.6|1.55
1.65|1.7|1.65|1.7|1.65
1.75|1.8|1.75|1.8|1.75
1.85|1.9|1.85|1.9|1.85
1.95|2.0|1.95|2.0|1.95
# ./sqlite3
SQLite version 3.28.0 2019-04-16 19:49:53
Enter ".help" for usage hints.
Connected to a transient in-memory database.
Use ".open FILENAME" to reopen on a persistent database.
sqlite>
sqlite> create table t4 (id1 real, id2 number(10,2), name varchar(100));
sqlite> insert into t4 values (1.05, 1.05, '1.05');
sqlite> insert into t4 values (1.15, 1.15, '1.15');
sqlite> insert into t4 values (1.25, 1.25, '1.25');
sqlite> insert into t4 values (1.35, 1.35, '1.35');
sqlite> insert into t4 values (1.45, 1.45, '1.45');
sqlite> insert into t4 values (1.55, 1.55, '1.55');
sqlite> insert into t4 values (1.65, 1.65, '1.65');
sqlite> insert into t4 values (1.75, 1.75, '1.75');
sqlite> insert into t4 values (1.85, 1.85, '1.85');
sqlite> insert into t4 values (1.95, 1.95, '1.95');
sqlite>
sqlite> select id1, round(id1,1), id2, round(id2,1), name from t4;
1.05|1.1|1.05|1.1|1.05
1.15|1.1|1.15|1.1|1.15
1.25|1.3|1.25|1.3|1.25
1.35|1.4|1.35|1.4|1.35
1.45|1.4|1.45|1.4|1.45
1.55|1.6|1.55|1.6|1.55
1.65|1.6|1.65|1.6|1.65
1.75|1.8|1.75|1.8|1.75
1.85|1.9|1.85|1.9|1.85
1.95|1.9|1.95|1.9|1.95
可以看到在老的版本上面(小于等于3.28),sqlite的四舍五入有问题,且sqlite的小数采用的是双精度,sqlite的官方文档(https://www.sqlite.org/datatype3.html)也记录了:“REAL. The value is a floating point value, stored as an 8-byte IEEE floating point number.”。number跟real的表现一致。不过新的版本没四舍五入的问题。
sqlite是个单文件库,如果用新版本的库打开旧版本的保存的db文件,以及用老版本打开新版本保存的db文件,又是什么情况。我这里直接说结论,我用3.36去打开用3.28保存的db文件,四舍五入没问题,用3.28打开3.36保存的db文件,四舍五入有问题,这说明四舍五入的特性与db文件无关,只与驱动版本有关。从sqlite的release ( https://www.sqlite.org/changes.html )里面也可以看到sqlite在这方面做的优化。
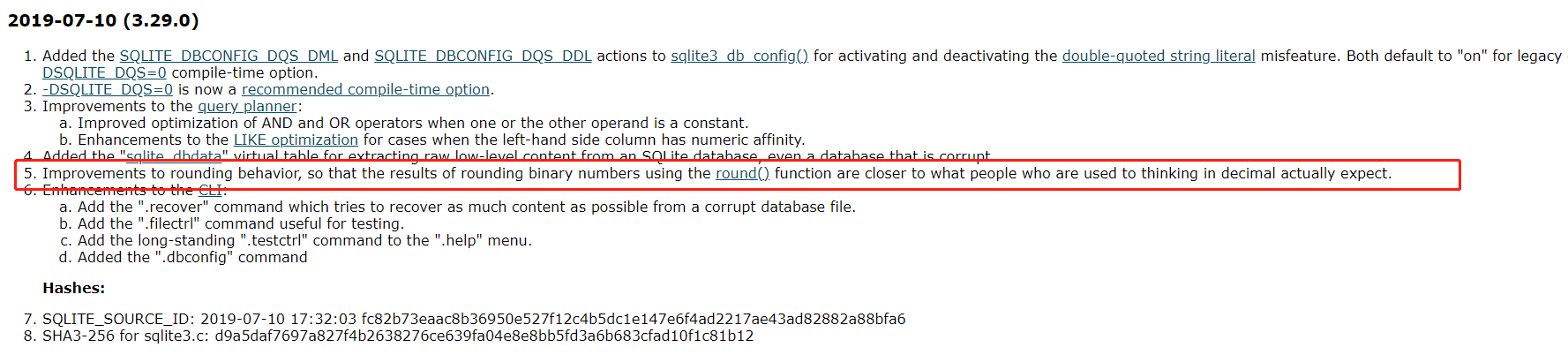
六、总结
- 当小数的四舍五入最后一位是5的时候,是否进1,要看这个小数实际在计算机中存储的值。
- 对于数据库来说,oracle没有这方面的问题,mysql尽量使用定点数,sqlite升级到新的驱动版本。
- 至于编程语言的四舍五入问题,大家自己想办法吧。
本文参考:
https://www.sqlite.org/datatype3.html
https://docs.python.org/3/tutorial/floatingpoint.html#tut-fp-issues
https://www.h-schmidt.net/FloatConverter/IEEE754.html
https://www.binaryconvert.com/result_double.html?decimal=049046052053






