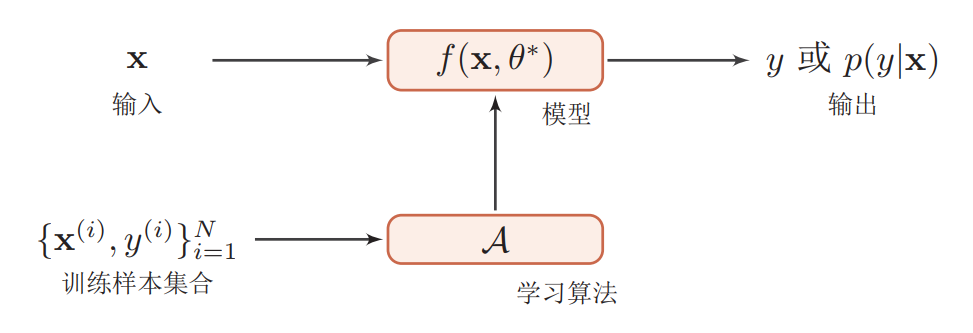
为什么需要正则化

正则化是为了防止过拟合， 进而增强泛化能力^[1]。

泛化误差（generalization error）亦即测试误差（test error），指使用训练数据训练的模型在测试集上的表现。

风险函数

损失函数（Loss function）旨在衡量模型 预测值 与真实值  的差异度，亦作代价函数（Cost function）。例如，交叉熵损失函数一般用于分类问题。损失函数只能度量模型一次预测的好坏，因此需要风险函数来度量平均意义下的模型预测好坏。

机器学习三要素^[2]  
机器学习方法大致分为三个基本要素：模型、学习准则、优化算法。
1. 模型就是要学习的条件概率分布或决策函数；
2. 统计学习需要确定使用什么样的准则进行学习或者选择最优模型。
3. 机器学习的训练过程其实就是最优化问题的求解过程。

期望风险

由于模型的输入、输出是随机变量, 遵循联合概率分布 , 所以损失函数的期望 (平均) 表达为：

这是理论上模型 关于联合分布 的平均意义下的代价损失，称为风险函数（risk function）或期望损失 (expected loss)。

经验风险

衡量模型在训练集中所有样本的预测性能的一个直接方法是平均损失，即将问题转化为经验风险 最小化问题，表示为：

其中， 是训练样本， 是损失函数， 是假设空间， 表示训练集中样本的数目。

假设空间  机器学习的目标是找到一个模型来近似真实映射函数 或真实条件概率分布 。由于我们不知道真实的映射函数 或条件概率分布 的具体形式, 只能根据经验来确定一个假设函数集合 , 这个集合称为假设空间 (Hypothesis space)。假设空间的确定意着学习范围的确定。假设空间 通常为一个参数化的函数族

其中， 表示假设空间中的模型 表示一组可学习的参数 为参数的数量。 为 维欧式空间，称为参数空间。

对上式的直观理解是，希望在假设空间 找到一个最优的模型函数 ，使得它在训练样本上的误差 最小。

结构风险

经验风险只能够保证模型在训练集上的误差尽可能小，而不能保证其在测试集中表现得好。也就是让泛化误差（Generalization error）亦即测试误差（Test error）尽可能小，指使用训练数据训练的模型在测试集上的表现。

需要在经验风险的基础上添加一个正则化项来限制模型能力，使其不要过度地最小化经验风险 。即，结构风险 =经验风险+正则化项，结构风险最小化等价于正则化，表示为：

其中， 为正则项。 表示正化参数，用来控制正则化强度，以权衡经验风险和模型复杂度。 可以理解为函数的复杂度，通常有 和 正则化。

理解模型的复杂度^[3]   设 为目标决策函数， 为学习到的决策函数， 表示训练集， 表示全集。训练过程只能保证 在训练集上与 保持一致，而其终极目标是让它们在全集上尽可能保持一致，分别使用 和 表示：

尽管加了正则化后的在训练集中的   一致性上升，但是有可能在全集中的 不一定降低。

训练集大小 越大，模型的复杂度 越小；VC 维度越大，模型的复杂度 越大；最小化 即为经验风险最小化准则。

和 正则化

在机器学习中，曼哈顿距离和欧式距离常用作 和 正则化，即在原来的目标函数的基础上，加上一些正则化项或者称为模型复杂度惩罚项。在经验风险最小化的基础上，尽可能采用简单的模型（结构风险最小化），以此提高泛化预测精度^[4]。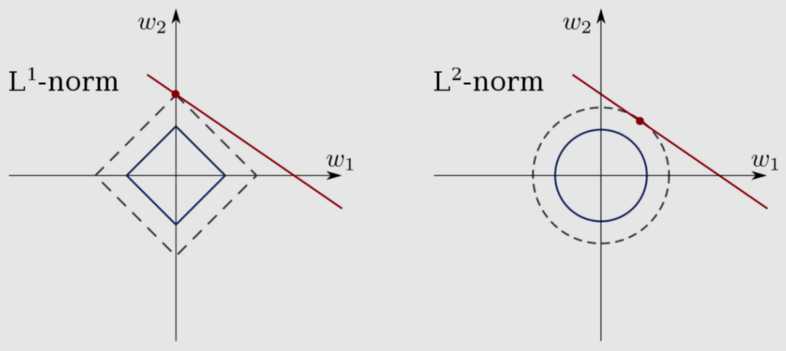几乎对于很多原函数等高曲线，和某个菱形相交的时候及其容易相交在坐标轴，也就是说最终的结果，解的某些维度及其容易是0，因此 正则化更容易得到稀疏解（解向量中0比较多）的原因。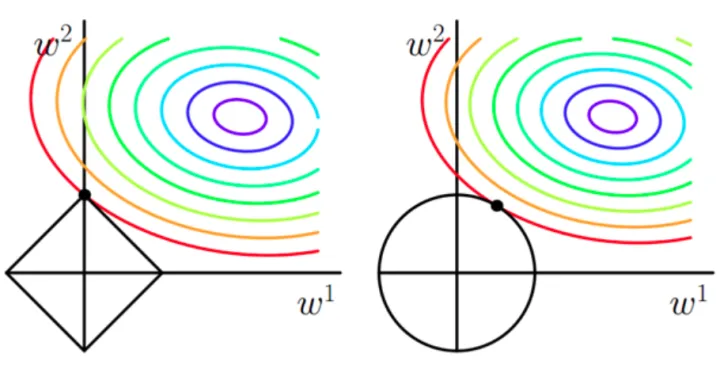与 正则化相比， 范数不容易交在坐标轴上，但是仍然比较靠近坐标轴。因此这也就是 范数能让解比较小，但是比较平滑（不等于0）。

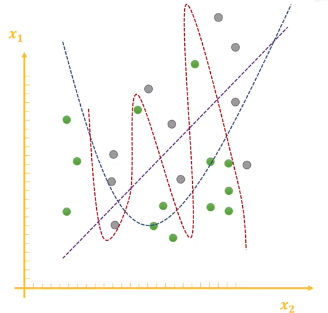
直观理解

直线：欠拟合；高次曲线：过拟合。加入正则化项有利于模型复杂度的降低，从而让拟合曲线逼近二次曲线。

正则化 ，那么 ，只惩罚大于 1 的高次项。

参考资料