Kaggle知识点：NumExpr加速Numpy计算

NumExpr
是 NumPy
的快速数值表达式求值器。NumExpr
对使用表达式（如3*a+4*b
）进行计算，并且比在Python
中执行相同的计算使用更少的内存。

NumExpr 基础使用

NumExpr
拥有更好的性能的主要原因是它避免了为中间结果分配内存，这导致减少一般的内存访问。因此NumExpr
最适用于大型数组。

安装方法：

pip install numexpr

使用案例：

import numpy as np
import numexpr as ne

a = np.random.rand(10000)
b = np.random.rand(10000)

# 等同于 2*a + b**10
ne.evaluate("2*a + b**10")

NumExpr 数据格式

NumExpr
仅在内部使用以下类型运行：

• 8 位布尔值 (bool)
• 32 位有符号整数（int 或 int32）
• 64 位有符号整数（long 或 int64）
• 32 位单精度浮点数（float 或 float32）
• 64 位双精度浮点数（double 或 float64）
• 2x64 位双精度复数（complex 或 complex128）
• 原始字节串 (str)

如果表达式中的数组不匹配这些类型中的任何一种，它们将被向上转换为上述类型之一.

NumExpr 运算符

NumExpr 支持下面列出的一组运算符：

• Logical operators: &, |, ~
• Comparison operators: <, <=, ==, !=, >=, >
• Unary arithmetic operators: -
• Binary arithmetic operators: +, -, *, , **, %, <<, >>

NumExpr 函数运算

NumExpr 支持下列内置函数：

• where
  
• sin,cos,tan
  
• arcsin,arccos,arctan
  
• arctan2
  
• sinh,cosh,tanh
  
• arcsinh,arccosh,arctanh
  
• log,log10,log1p
  
• exp,expm1
  
• conj,real,imag,complex
  
• contains
  

NumExpr 使用案例

num = 10000
a = np.random.rand(num)
b = np.random.rand(num)

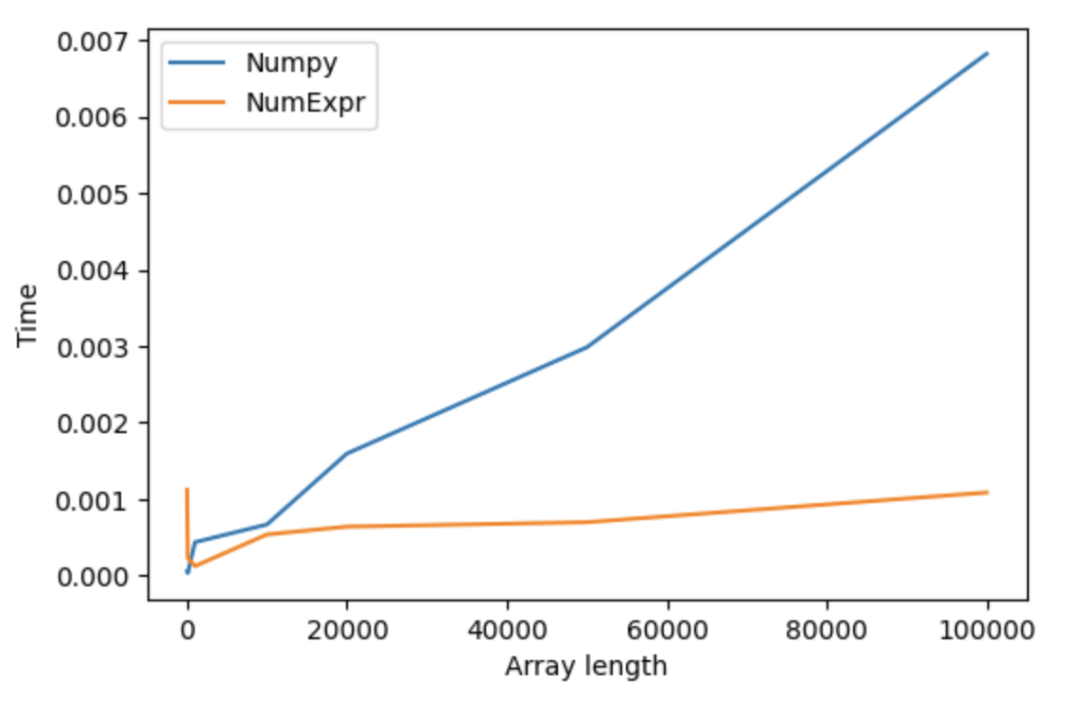
_ = 2*a + b**10 + np.log(a) * np.log(b)
_ = ne.evaluate("2*a + b**10 + log(a) * log(b)")

num = 10000
a = np.random.rand(num)
b = np.random.rand(num)

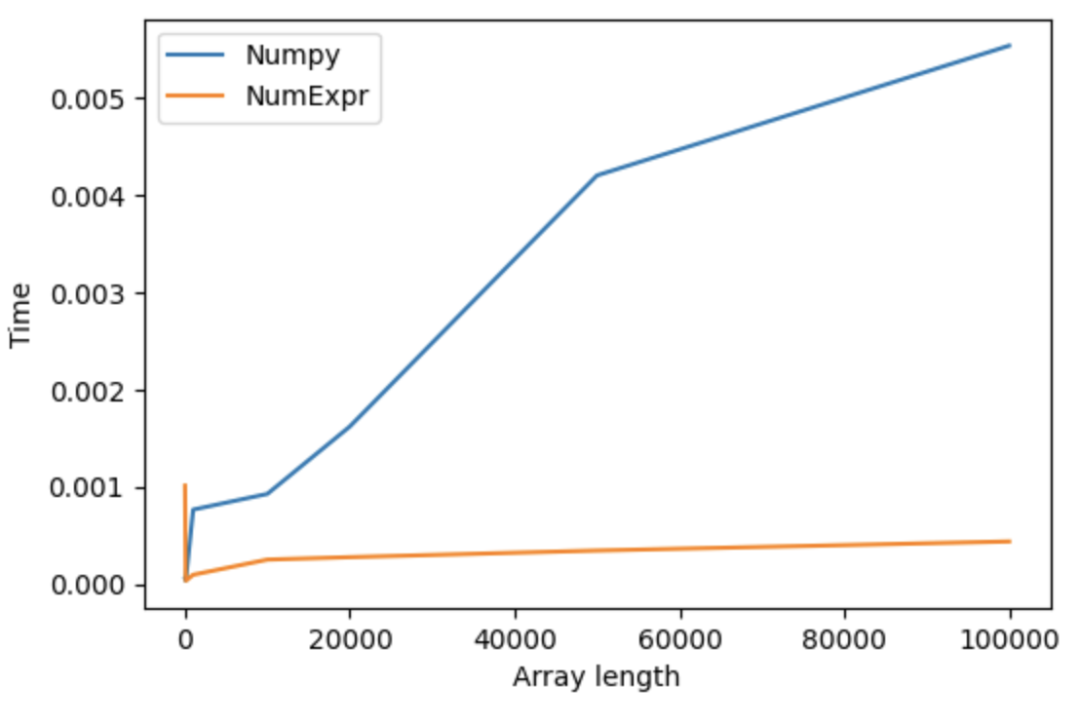
_ = 2*a + b**10 + np.abs(a)
_ = ne.evaluate("2*a + b**10 + abs(a)")

num = 10000
a = np.random.rand(num)
b = np.random.rand(num)

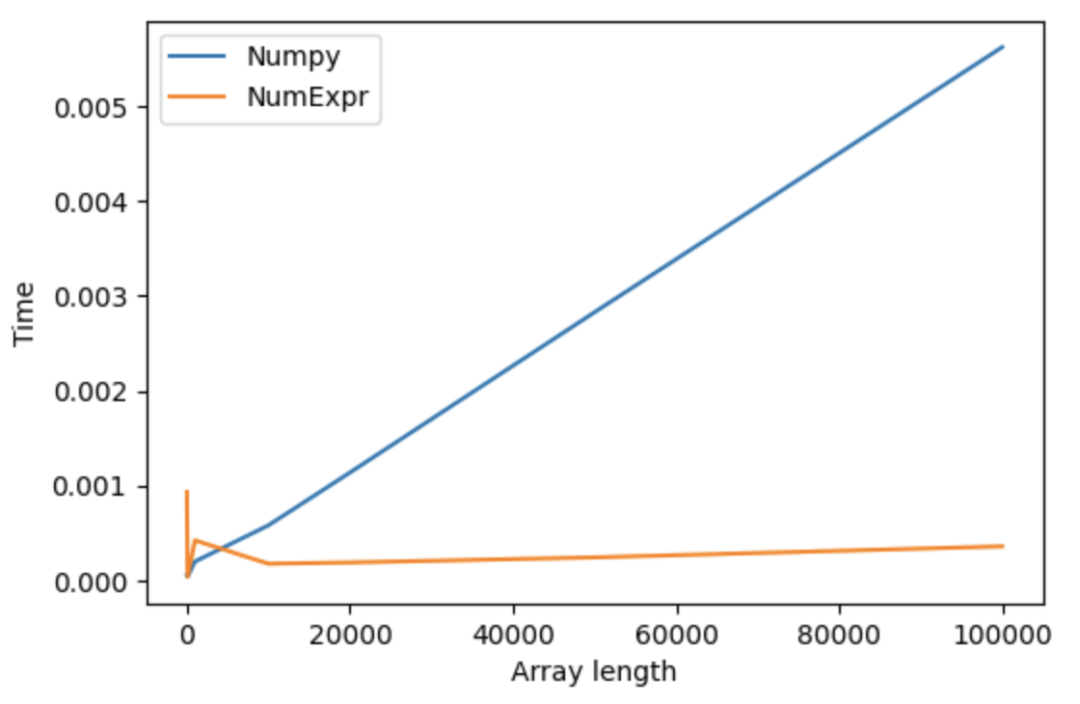
_ = 2*a + b**10 + a*b
_ = ne.evaluate("2*a + b**10 + a*b")

num = 10000
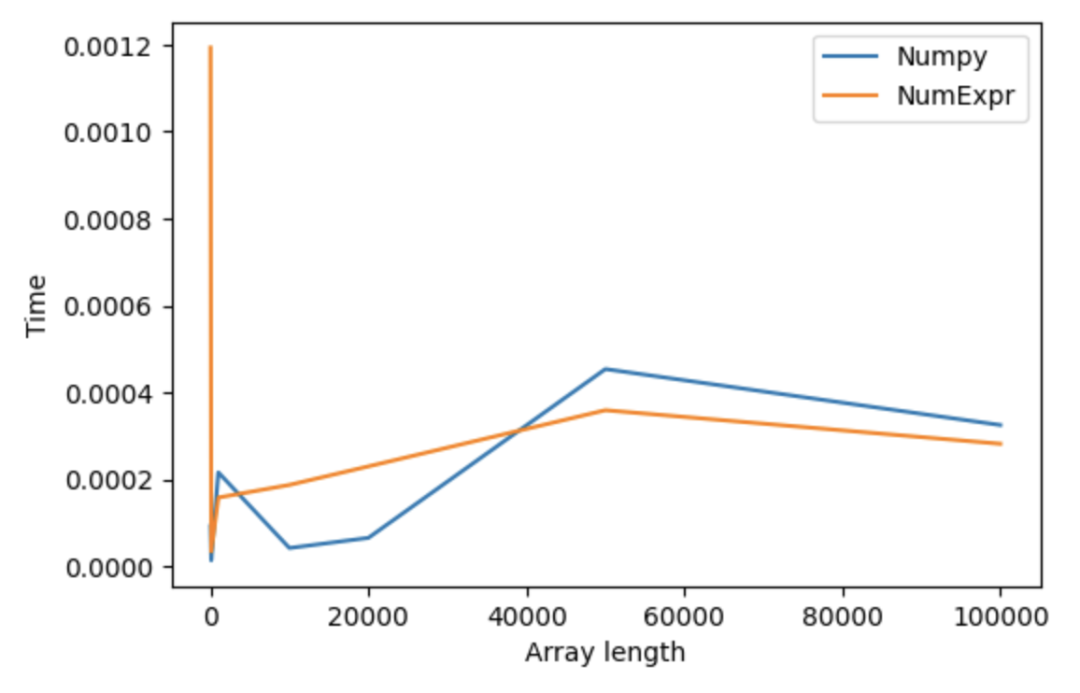
a = np.random.rand(num).astype(int16)
b = np.random.rand(num).astype(int16)

_ = 2*a + b**10 + a*b
_ = ne.evaluate("2*a + b**10 + a*b")

num = 10000
a = np.random.rand(num).astype(int32)
b = np.random.rand(num).astype(int32)

_ = 2*a + b**10 + a*b
_ = ne.evaluate("2*a + b**10 + a*b")

num = 10000
a = np.random.rand(num).astype(np.bool8)
b = np.random.rand(num).astype(np.bool8)

_ = a | b
_ = ne.evaluate("a | b")

NumExpr 使用总结

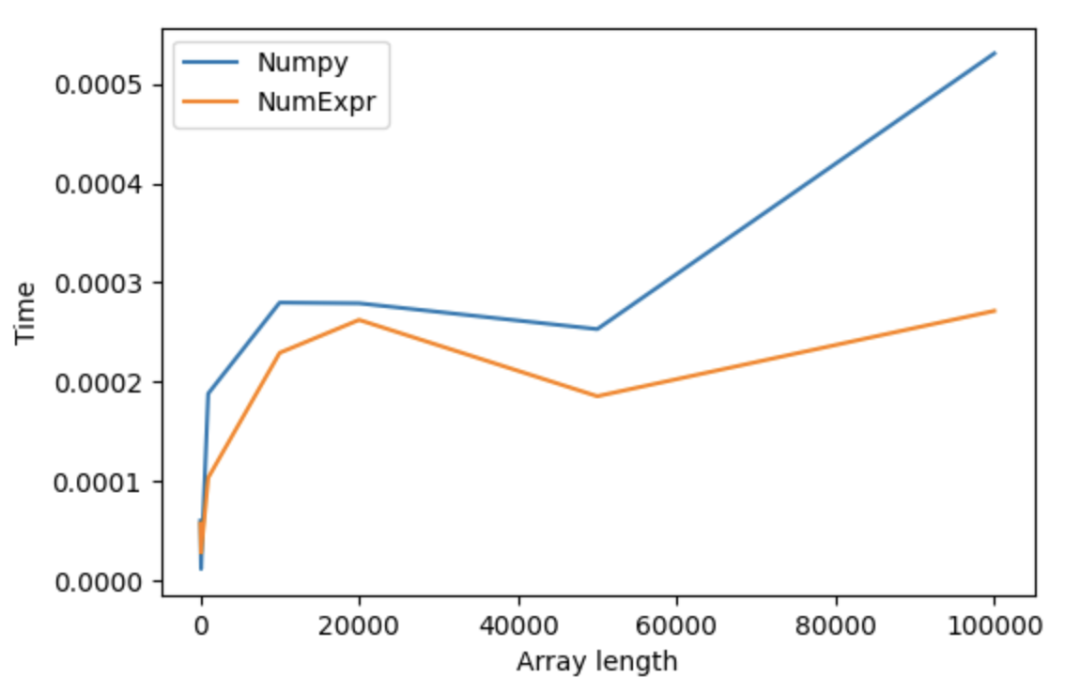
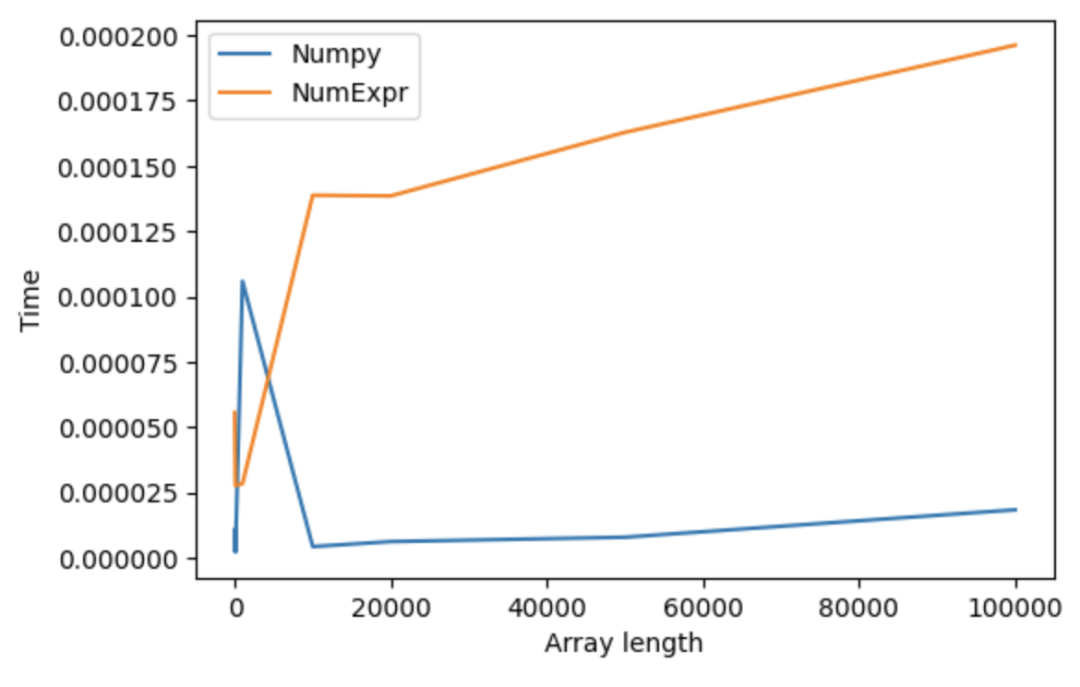
1. NumExpr
   支持基础的运算加速，且对32位浮点数加速比较明显，但对不同的格式有不同的加速比。

2. NumExpr
   只支持基础的运算函数，复杂的运算（如循环和索引）逻辑并不支持。

3. 在数据量比较小的情况下，NumExpr
   加速并不明显。且在不同机器，需要设置不同的进程数。

更多干货获取

1. Kaggle竞赛2022年鉴：公众号回复kaggle2022
   获取
2. 推荐系统知识卡片：公众号回复推荐系统
   获取
3. 数据科学速查表（传统CTR、深度学习CTR、Graph Embedding、多任务学习）：公众号回复速查表
   获取
4. 历届腾讯广告算法大赛答辩PPT：公众号回复腾讯赛
   获取
5. KDD Cup历史比赛合集：公众号回复KDD2020
   获取

学习交流群已成立

学习推荐系统，算法竞赛，组队参赛

添加👇微信拉你进群