暂无图片
暂无图片
暂无图片
暂无图片
暂无图片
首页 / 论文导读 | 连续图上的子图匹配（Continuous Subgraph Matching）

论文导读 | 连续图上的子图匹配（Continuous Subgraph Matching）

图谱学苑 2023-05-28
535

连续图上的子图匹配（Continuous Subgraph Matching） 连续子图匹配（CSM）算法是一类在线地查找给定模式在数据图流中的出现实例的算法。数据图流既对数据图的修改以数据流的形式不断给出。本文将介绍针对这个问题


背景介绍

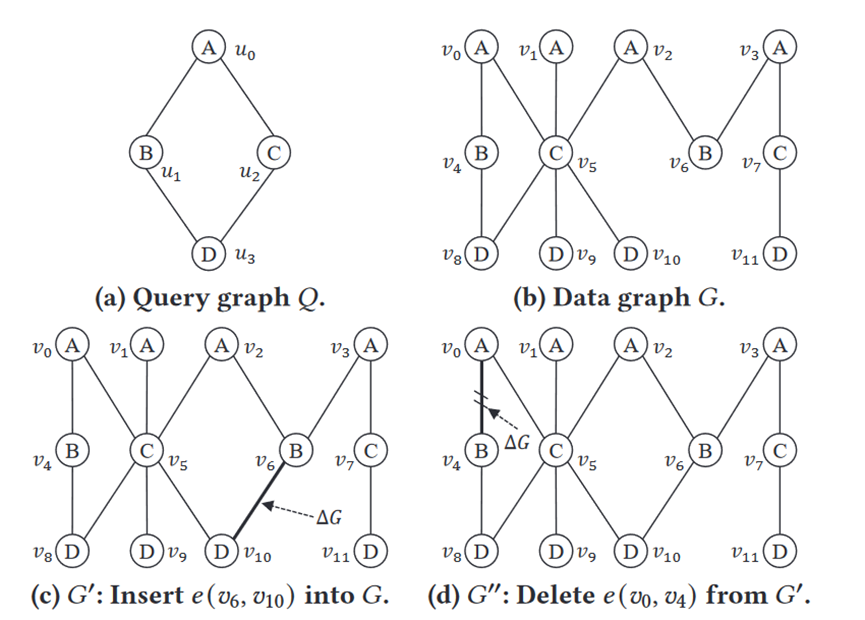
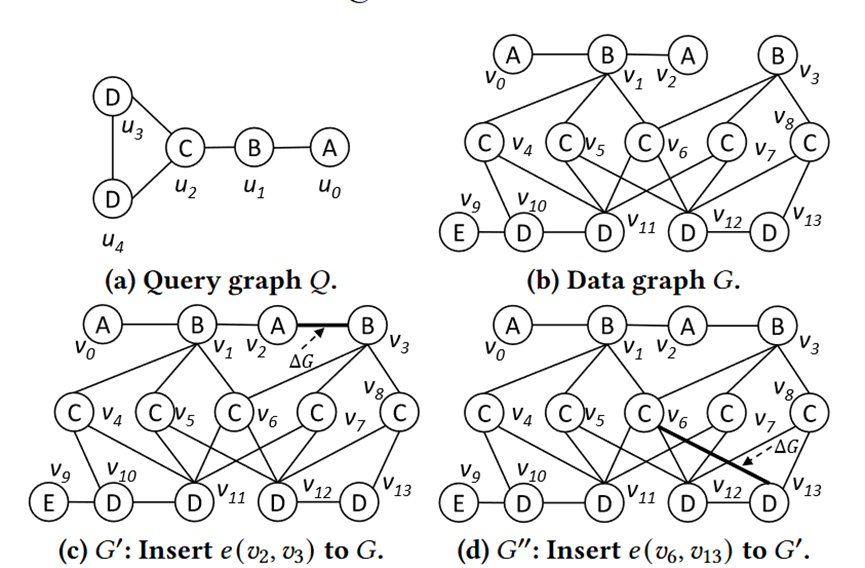
子图匹配可以看成是找到一个映射函数，将查询图上的点映射到数据图上，满足标签的要求以及连边的要求。例如上图中的(a)(b)，{ u0à0, u2à5, u3à8, u1à4}就是一个满足要求的映射。

子图匹配问题的主要的优化方向有，设计剪枝策略，优化枚举顺序，以及通过辅助数据结构减少重复的计算等等。

而连续图上的子图匹配，每次有一条边或者多条边的修改，然后要求包含这些发生改变的边的匹配实例。

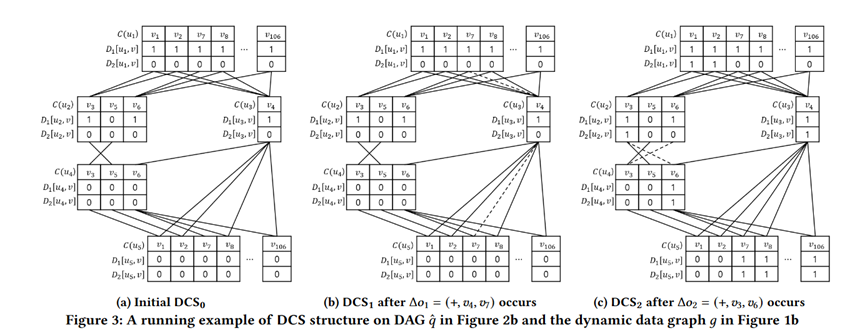
c图是一个添加的例子，d图是一个删除的例子，先找到包含删除的边的匹配实例，然后再执行删除。

现有的关于CSM的相关工作一般会包含上图中的几个步骤。左上角是原图G，基于G维护一些辅助数据结构A，用来加速后续的查询。当数据图发生更新的时候，辅助数据结构也会进行相应的更新。最后，使用原图的信息和辅助数据结构，进行枚举得到匹配实例。
动态图上的研究工作大体可以分成两类，第一类是不维护索引结构每次重新计算的，例如IncIsoMatch, Graphflow, RapidFlow等。第二类是设计一些特殊的辅助索引结构加速计算的，有SJ-Tree, TurboFlux, IEDyn, SymBi。
动态图上的工作主要用到的优化方法包括匹配顺序的选取，避免对同构结构的重复枚举，用一些辅助结构对候选集进行筛选，以及一些其他的减少重复计算，减小搜索空间的方法。

Graphflow采用了worst case optimal join的执行顺序，减少匹配的中间结果。
另一种执行顺序是binary join，每次加入一条边，或者将两个部分匹配合并起来。

如图，Binary join在做三角形查询的时候，查这个链的时候可以有很多中间结果（假设每条边有N个实例，那么在加入第三条边之前可能会有N^2个实例）。而在worst case optimal join中，每次加入一个点，需要做multiway-join。在上述的例子中，因为后两条边是通过multiway-join一起考虑的，所以最多只会有N^1.5个实例。
Graphflow的另一个优化点是避免重复的实例。例如当前的两条边对应的实例是（A，da），（B，db）。预期得到的是(da,B)(A,db)(da,db)。但是直接查询会得到所有实例（包括(A，B））。graphflow的处理方法抽象来看是给每一条匹配边顶一个顺序，让每个新增实例被他边id最小的那条边匹配到。（既这条边只包含新增实例，之前的边包含所有实例，之后的边只包含旧的实例）。

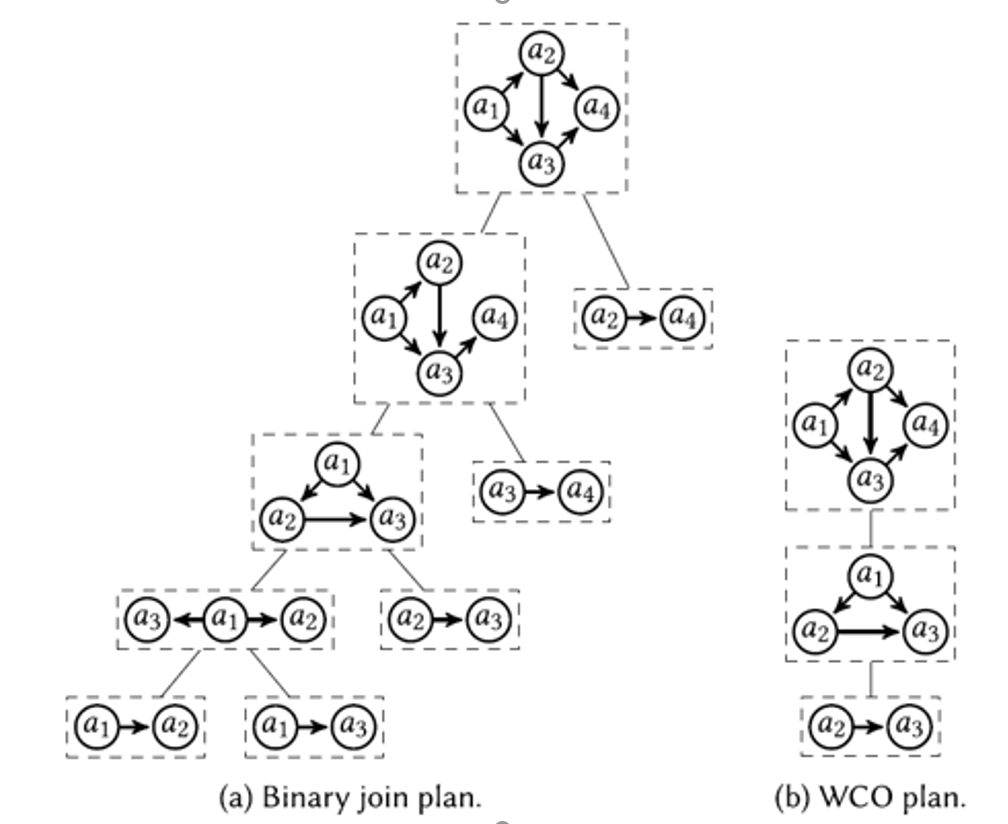
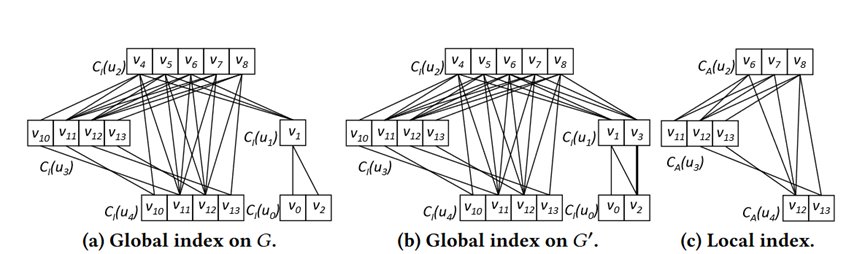
这一篇工作的主要思路是构建一个Subgraph join tree，一个基于binary join plan构成的左伸树，叶子节点是每一条边，匹配的部分结果存储在非叶子节点上。当有一条边发生更新时，只需要更新从当前点到根的路径上的节点。

如上图，如果likes这条边新增了一个实例，那么只有它到根的路径上的结果可能发生改变，其他的保持不变。

TurboFlux的核心思路是维护一个辅助数据结构，用来记录当数据点v匹配查询点u是，是否存在匹配的子结构（如果不存在则可以剪枝掉）。
这篇工作首先考虑查询图是树的情况，如果是图则考虑他的一个生成树。最后再检查非树边。
每个数据图中的点维护一个和查询图一样大的辅助数据结构，记录信息在查询的时候进行筛选。
只考虑树的情况，每个点维护两个状态，一个是向下的子树是否都匹配上了，一个是是否有到根的路径。每次添加边后，首先维护是否有根到当前点的所有子树的路径。走到最后一个状态发生改变的点，则这个点一定是叶子节点。然后从叶子节点网上更新这个子树是否都匹配上了。如果匹配到非树边，则直接从两个点开始更新。相当于不利用这个非树边来过滤。如下图。

IDEyn用的是和TurboFlux类似的思路。不同点在于他只维护向下是否成立的状态。此外，这两个工作关注的是在关系数据库上的无环的查询，可以抽象成图数据库中的树的查询。

在后续的研究中发现，对于非树边的检测在很多查询中占据了大量的时间开销。利用上非树边的信息可以得到更好的剪枝效率。因此SymBi考虑利用上非树边的信息（构建一个有向无环图）进行过滤。此时记录的信息变成了一个必要不充分条件，因此只能用来剪枝，减少候选集的大小。作者定义了一个名为Dynamic candidate space(DCS) structure的数据结构来维护这个基于有向无环图结构得到的辅助信息。如下图

DCS的基本结构，首先通过节点和边的标签，将查询图中的每个点的候选点集存储在一起。然后对于原图中的边，对应的查询图中的点有边相连时才连边。将原始的数据图转换成一个等价的辅助查询图。后续操作只需要在这个图上执行。在此基础上，维护D1和D2两个辅助的筛选结构。
在维护DCS的两个D辅助结构的过程中，每条边有一个count记录有几个成立的，来处理删除的情况的维护。当每条边都有至少一个记录时，这两个点的辅助结构才标记为存在匹配子结构。
此外，作者还使用了一个剪枝策略，命名为Isolated Vertices。核心思想是最后匹配叶子节点，因为叶子节点对其他部分不会有影响。如果叶子节点匹配到多个点，会带来多倍的查询。如果叶子节点匹配不到点，则可以提前剪枝。优化的点：拆成多个子部分，最后做笛卡尔积。类似DAF这个工作的failing set优化。
DAF的failing set优化的动机如下图：

若先匹配上了u1-v1，u4-v1003，然后匹配u2-v2，考虑这样一种情况：按照matching order匹配，某个前缀的所有后续都匹配不了。这个时候，如果前缀的最后一个点和这些匹配不了的情况无关的话，则这个点无论匹配什么都匹配不上，所以这个点不需要枚举下一个候选点。

RapidFlow并没有设计复杂的辅助结构来剪枝。这个工作的核心思想有两个：
1、之前的所有方法都是从更新的边开始搜索的，这限制了对matching order的优化方法的使用。
2、之前的方法没有对同构的搜索结构进行处理。导致同构的结构被重复枚举。
他的主要的两个贡献点，一个是两层的索引结构。
Global index和Symbi的结构类似，将原始的数据图转换成一个由查询图的点，
Local index是从global index中抽出当前的更新边影响到的一个子图。

这个是他的两层索引结构的一个示意。右上角是数据图和查询图，下边的是他的两层索引结构。Global index和SymBi这个工作中的第一步将原图转换成一个等价的辅助图的结构类似。
Global index就是把每个query point的候选点以及他们之间的连边存起来。
Local index则是，比如我更新的是v2-v3这条边，他可以匹配到q图中的u0和u1.  然后我把他们v2和v3的一条邻居中匹配到u1和u0的一跳邻居的点抽出来。这里就是匹配上u2这个点，就是v6，v7，v8
然后继续匹配u2的邻居u3和u4，u3能匹配上的是v11，v12，v13，然后按照wcoj的顺序，匹配u4，要求和u3和u2都有连边，从global index中找符合条件的就是v12和v13
第二个贡献是减少对自同构结构的重复枚举。如图

U3和u4是对称的，所以存在很多匹配，他们只有u3和u4不同，但是却需要做两边搜索。如果我们能识别出u3和u4是对称的，那只需要求出一个实例，然后交换u3和u4的匹配点就可以得到所有实例。
当插入的边是u3-u4时，我们会发现这个边也匹配上了u4-u3，所以只需要做u3-u4的搜索，然后做一个转换就能得到u4-u3的结果。
具体的处理方法是，将得到的匹配实例和查询图做匹配。如果e在Q的一个同构中可以匹配上e‘，那么匹配e的答案和匹配e’的答案是一样的。
其他一些subgraph matching或者GPM的工作中也有使用称为symmetry breaking的优化方法。做法是定义一个被称为symmetry order的偏序关系，要求匹配实例必须满足这个偏序关系。这样就使得原来的自同构结构中只有一个能满足要求的偏序关系。


参考文献

X. Sun, S. Sun, Q. Luo, and B. He, “An in-depth study of continuous subgraph matching,” Proc. VLDB Endow., vol. 15, no. 7, pp. 1403–1416, Mar. 2022, doi: 10.14778/3523210.3523218.

C. Kankanamge, S. Sahu, A. Mhedbhi, J. Chen, and S. Salihoglu, “Graphflow: An Active Graph Database,” in Proceedings of the 2017 ACM International Conference on Management of Data, Chicago Illinois USA: ACM, May 2017, pp. 1695–1698. doi: 10.1145/3035918.3056445.

S. Choudhury, L. Holder, and G. Chin, “A Selectivity based approach to Continuous Pattern Detection in Streaming Graphs”.

K. Kim et al., “TurboFlux: A Fast Continuous Subgraph Matching System for Streaming Graph Data,” in Proceedings of the 2018 International Conference on Management of Data, Houston TX USA: ACM, May 2018, pp. 411–426. doi: 10.1145/3183713.3196917.

M. Idris, M. Ugarte, and S. Vansummeren, “The Dynamic Yannakakis Algorithm: Compact and Efficient Query Processing Under Updates,” in Proceedings of the 2017 ACM International Conference on Management of Data, Chicago Illinois USA: ACM, May 2017, pp. 1259–1274. doi: 10.1145/3035918.3064027.

[1]

M. Idris, M. Ugarte, S. Vansummeren, H. Voigt, and W. Lehner, “Conjunctive Queries with Theta Joins Under Updates.” arXiv, May 23, 2019. Accessed: Apr. 10, 2023. [Online]. Available: http://arxiv.org/abs/1905.09848

S. Min, S. G. Park, K. Park, D. Giammarresi, G. F. Italiano, and W.-S. Han, “Symmetric continuous subgraph matching with bidirectional dynamic programming,” Proc. VLDB Endow., vol. 14, no. 8, pp. 1298–1310, Apr. 2021, doi: 10.14778/3457390.3457395.

M. Han, H. Kim, G. Gu, K. Park, and W.-S. Han, “Efficient Subgraph Matching: Harmonizing Dynamic Programming, Adaptive Matching Order, and Failing Set Together,” in Proceedings of the 2019 International Conference on Management of Data, Amsterdam Netherlands: ACM, Jun. 2019, pp. 1429–1446. doi: 10.1145/3299869.3319880.

S. Sun, X. Sun, B. He, and Q. Luo, “RapidFlow: an efficient approach to continuous subgraph matching,” Proc. VLDB Endow., vol. 15, no. 11, pp. 2415–2427, Jul. 2022, doi: 10.14778/3551793.3551803.

欢迎关注北京大学王选计算机研究所数据管理实验室微信公众号“图谱学苑“
实验室官网：https://mod.wict.pku.edu.cn/
微信社区群：请回复“社区”获取

实验室开源产品图数据库gStore：
gStore官网：https://www.gstore.cn/
GitHub：https://github.com/pkumod/gStore
Gitee：https://gitee.com/PKUMOD/gStore






matching
文章转载自图谱学苑，如果涉嫌侵权，请发送邮件至：contact@modb.pro进行举报，并提供相关证据，一经查实，墨天轮将立刻删除相关内容。

评论