前言
求任意位置的斐波那契数,最常见的做法是使用递归,这种做法虽然可以得到结果,但是它的性能很差。
本文跟大家分享一种性能较好的解决方案,欢迎各位感兴趣的开发者阅读本文。
概念
我们先来看下什么是斐波那契数列,有一个数列它的0号位置的值是0,1号位置的值是1,当要求的位置(n)大于1时,其值为(n-1)+(n-2)
。
我们举个例子来说明下:
我们要求5号位置的斐波那契数,那么我们就要求出5-1
位置的斐波那契数和5-2
位置的斐波那契数。
4号位置的斐波那契数为 f(4-1) + f(4-2)3号位置的斐波那契数为 f(3-1) + f(3-2)2号位置的斐波那契数为 f(2-1) + f(2-2)1号位置的斐波那契数为 10号位置的斐波那契数为 0
如上所示,我们想知道5号位置的斐波那契数就得先知道4号和3号位置的斐波那契数,以此类推直到1号位置和0号位置,那么:
2号位置的斐波那契数就为: 1 + 0 = 13号位置的斐波那契数就为: 1 + 1 = 24号位置的斐波那契数就为: 2 + 1 = 35号位置的斐波那契数就为: 3 + 2 = 5
解决方案
接下来,我们来详细讲解下这这个问题的解决方案。
递归解决
很多教材在讲解递归时,都会使用求斐波那契数作为例子,因此许多开发者在看到这道题的时候,一下子就能想到这道题应该用递归来解。
在我的另一篇文章:递归的理解与实现 中详细讲解了斐波那契数列的递归解法。此处不做过多阐述,只画一下上述例子的递归树,如下所示:
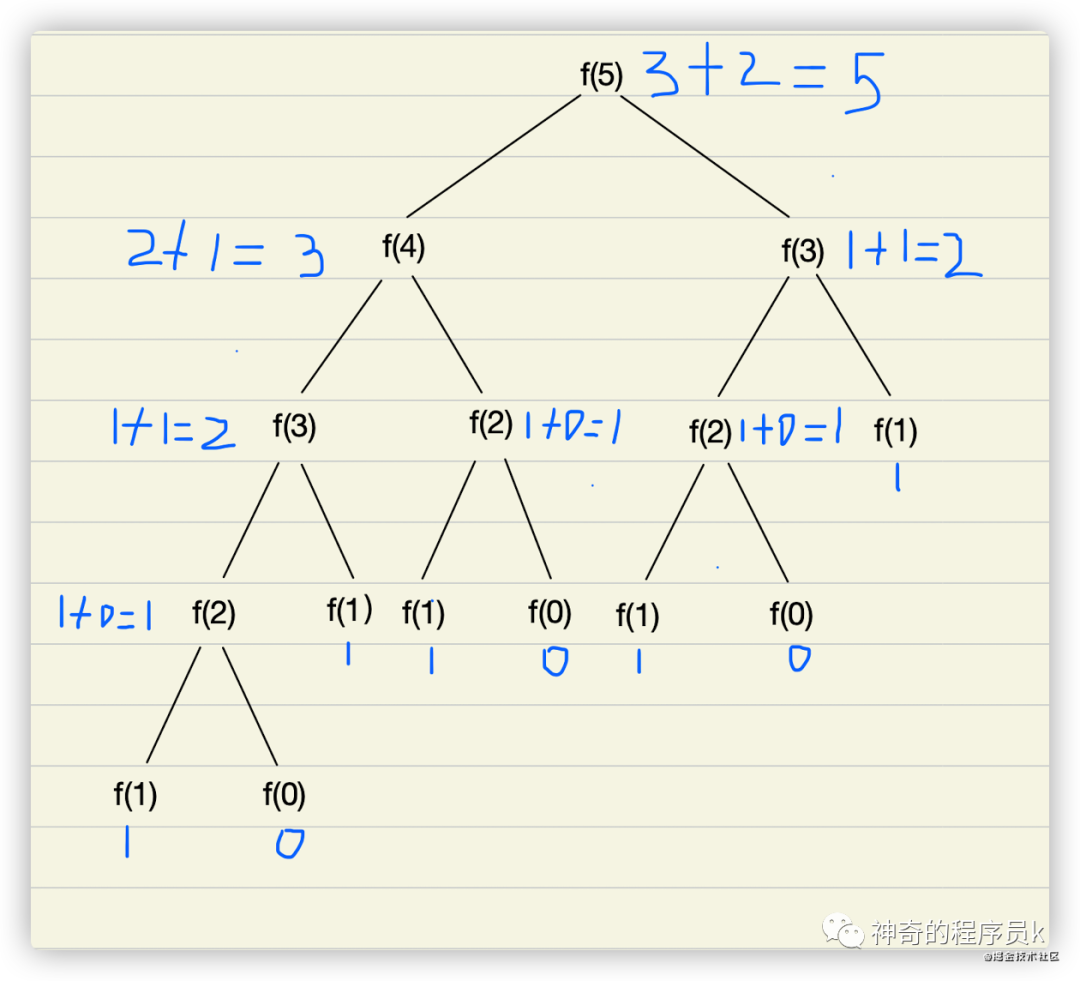
观察上述递归树,我们会发现有好多节点都是重复的,而且重复的节点数会随着n的增大而急剧增加,也意味着计算量会随着n的增大而急剧增大,因此它的性能是非常差的。
自下而上
上述代码之所以慢,是因为重复的计算太多了,我们可以采用从下往上计算的方式,首先根据f(0)和f(1)算出f(2),再根据f(1)和f(2)算出f(3),以此类推就可以算出第n项了,它的时间复杂度是O(n)
,我们把这种解法称为自下而上。
我们画个图来讲解下上述思路:

实现代码
我们分析完上述思路后,接下来就可以将其转换为代码了,如下所示:
export default class Fibonacci {
private readonly index: number;
constructor(index: number) {
this.index = index;
}
/**
* 自下往上实现
* 实现思路:
* 1. 根据f(0)和f(1)算出f(2)
* 2. 再根据f(1)和F(2)算出f(3)
* 3. 以此类推算出第n项
* 时间复杂度分析:它从第0项遍历到最后一项,因此时间复杂度为O(n)
*/
public bottomUp(): number {
const result: Array<number> = [0, 1];
if (this.index < 2) {
return result[this.index];
}
// f(n - 1)
let fibNMinusOne = 1;
// f(n - 2)
let fibNMinusTwo = 0;
let fibN = 0;
for (let i = 2; i <= this.index; ++i) {
// f(n) = f(n - 1) + f(n - 2)
fibN = fibNMinusOne + fibNMinusTwo;
// f(n - 2) = f(n - 1)
fibNMinusTwo = fibNMinusOne;
// f(n - 1) = f(n)
fibNMinusOne = fibN;
}
return fibN;
}
}
我们写个测试用例来执行下上述代码,检查下正确性,如下所示,我们需要求斐波那契数列的第100号位置的值:
import Fibonacci from "../Fibonacci.ts";
const fibonacciTest = new Fibonacci(100);
console.log("斐波那契数列的第1000号位置的值为:", fibonacciTest.bottomUp());
运行结果如下所示:
完整代码请移步:Fibonacci.ts
写在最后
至此,文章就分享完毕了。
我是神奇的程序员,一位前端开发工程师。
公众号无法外链,如果文中有链接,可点击下方阅读原文查看😊






