SVM详解(二)线性支持向量机与软间隔最大化

文章目录

• 文章目录

• 1. 线性支持向量机

• 2. 学习的对偶算法

• 3. 支持向量

1. 线性支持向量机

我们介绍了线性可分支持向量机模型，我们适用硬间隔最大化算法学得最好的分离超平面，但是该模型只适用于训练数据集是线性可分的情况，对于线性不可分训练数据集并不适用。通常情况下，线性不可分训练数据集，往往有一些特异点，将这些特异点去除之后，剩下大部分的样本点组成的集合是线性可分的，根据这个特性，我们允许一些特异点不满足函数间隔大于等于(即)的约束条件 ，来使用支持向量机达到分类训练数据集的目的。

为此，我们为训练数据集的每个样本点都引入一个松弛变量 ，使得函数间隔加上松弛变量，能满足间隔大于等于的约束条件，即   即

• 怎么理解这件事情呢，为了方便描述，我们将上面的式子两边同时除以，得到

  如下图所示，红色圆圈和五角星为特异点，白色则为正常的训练数据点

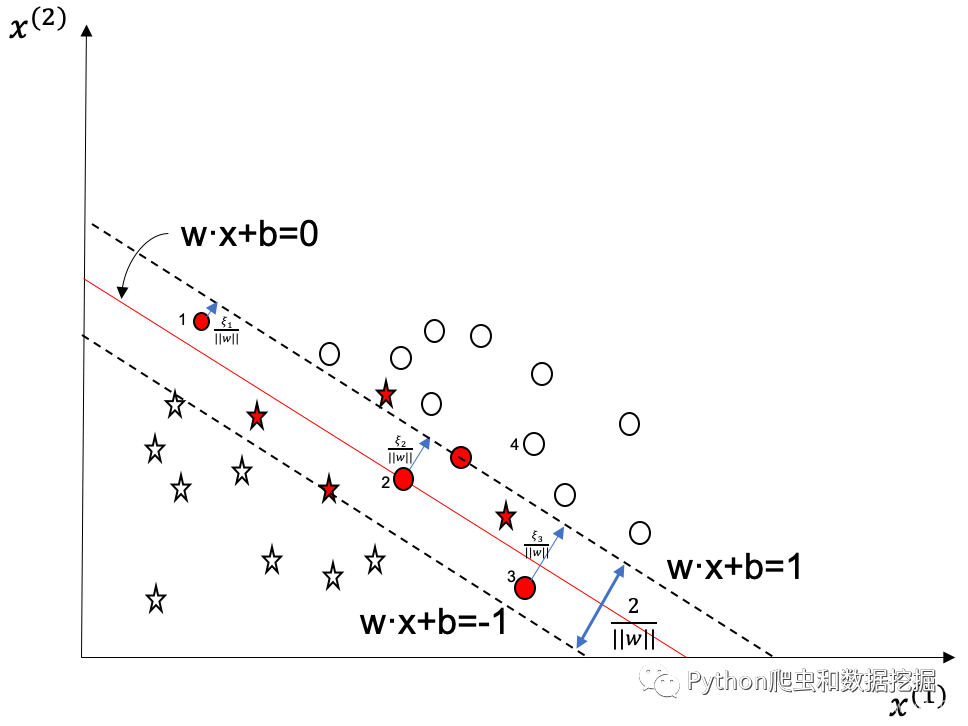
1. 对于图中的点，其位于间隔边界内部，且能够被正确分类，其距离分离超平面的距离可表示为为  ，我们通过对该点添加松弛变量，使得成立，即可以看做是将点沿所在直线方向朝正确分类的一侧移动至间隔边界上或者间隔边界外。至少应移动至间隔边界上，此时有
2. 对于图中的点，其位于分离超平面上，则其距离分离超平面的距离可表示为为  ，我们通过对该点添加松弛变量，使得成立，即可以看做是将点沿所在直线方向朝正确分类的一侧移动至间隔边界上或者间隔边界外。至少应移动至间隔边界上，此时有
3. 对于图中的点，被错误分类，其距离分离超平面的距离可表示为为  ，我们通过对该点添加松弛变量，使得成立，即可以看做是将点沿所在直线方向朝正确分类的一侧移动至间隔边界上或者间隔边界外。至少应移动至间隔边界上，此时有
4. 对于图中的点，其位于间隔边界外部，且能够被正确分类，其距离分离超平面的距离可表示为为  ，从图中可知，该点已经满足成立，此时有

通过引入松弛变量的几何意义解释，我们可以认为，松弛变量表征了样本点 如果是特异点的话，需要多少距离，才能被正确分类。

为此，我们需要对每个松弛变量，支付一个代价，目标函数由原来的 变成了

这里的其实就是正则项， 称为惩罚参数，一般由应用问题决定，值大时对误分类的惩罚增大，值小时对误分类的惩罚减小，最小化 其实就是使尽可能小即间隔尽量大，同时使误分类点的个数尽量小，则是调和二者的系数。

基于上面的思路，我们得到了线性不可分的线性支持向量机的学习最优化问题:

将这个问题作为原始问题，其仍是一个凸二次规划问题。相比于线性可分支持向量机的硬间隔最大化，我们将线性不可分的线性支持向量机学习问题称为软间隔最大化。显然，线性支持向量机是包含线性可分支持向量机的，由于现实中训练数据集往往是线性不可分的，因此线性支持向量机具有更广的适用性。

• 线性支持向量机定义

  对于给定的线性不可分的训练数据集，通过求解凸二次规划问题，即软间隔最大化问题，得到的分离超平面为

  以及相应的分类决策函数

  称为线性支持向量机

2. 学习的对偶算法

参照线性可分支持向量机，我们依然通过对偶问题来解线性支持向量机的原始问题。

首先构建拉格朗日函数，为：

其中，

根据拉格朗日对偶性，原始问题的对偶问题是极大极小问题：

所以，为了得到对偶问题的解，需要先求 对的极小，再求对的极大，

求

将拉格朗日函数 分别对 求偏导并令其等于，得到

得

将上式带入拉格朗日函数 ，得到

即

由于 中没有参数了，因此只需求 对的极大，即是对偶问题

该问题等价为

可以看出，线性支持向量机和线性可分支持向量机的对偶算法，就只有对偶变量的不等式约束条件不一样，前者是 ，后者是 。

原始问题的解应满足条件，得到：

由此得

其中至少有一个（用反证法，假设，则，很显然不是原始最优化问题的解，产生矛盾），对此有

，且

由于 可知 ，由于

所以有

此时

上式两边同时乘以

至此，我们解出了和的值，则最大间隔分离超平面为

分类决策函数可以写成

综上所述，我们得到了线性支持向量机的对偶学习算法，描述如下

• 算法2: 线性支持向量机的对偶学习算法

  输入：线性数据集，其中，

  输出：分离超平面和分类决策函数

  选择惩罚参数，构造并求解凸二次规划问题：

  求得最优解

  计算

  并选择的一个正分量适合条件，计算

  对任一适合条件的 ，均能按上式求出， 但是不同的样本点计算出的 并不一致，所以一般在所有满足条件的样本点上都计算，然后求平均值作为的最终值。

  求得分离超平面

  分类决策函数

3. 支持向量

在线性不可分的情况下，将对偶问题的解中对应于的样本点的实例称为「软间隔的支持向量」。有上述求解和的过程可知，线性支持向量机仍只与支持向量有关。

求解过程中的  条件中，需要满足

根据该式可知软间隔的支持向量 要么在间隔边界上，要么在间隔边界与分离超平面之间，要么在分离超平面误分一侧。 若，则 (上面根据条件求解时有证明)，此时有 则支持向量恰好落在间隔边界上；若，此时有 ，则分类正确，在间隔边界与分离超平面之间；若，此时有 ，则在分离超平面上；若，此时有 则位于分离超平面误分类一侧。这和我们在开篇引入松弛变量时的几何解释是一致的。

至此我们完成了线性支持向量机的算法介绍，线性支持向量机可以从多个角度进行解释，感兴趣的同学可以自行查阅相关资料。

当然，还有很多训练数据，属于非线性可分的情况，我们需要找到一个合适的超曲面来实现数据分类，我们如果处理这类数据呢？下一篇，我们将介绍SVM使用核函数处理非线性可分的情况。

本文参考李航老师的《统计学习方法》