




TKDE 2022-Multi-Scale Adaptive Graph Neural Network for Multivariate Time Series Forecasting.pdf
免费下载
1
Multi-Scale Adaptive Graph Neural Network for
Multivariate Time Series Forecasting
Ling Chen, Donghui Chen, Zongjiang Shang, Binqing Wu, Cen Zheng, Bo Wen, and Wei Zhang
Abstract—Multivariate time series (MTS) forecasting plays an
important role in the automation and optimization of intelligent
applications. It is a challenging task, as we need to consider
both complex intra-variable dependencies and inter-variable
dependencies. Existing works only learn temporal patterns with
the help of single inter-variable dependencies. However, there
are multi-scale temporal patterns in many real-world MTS.
Single inter-variable dependencies make the model prefer to learn
one type of prominent and shared temporal patterns. In this
paper, we propose a multi-scale adaptive graph neural network
(MAGNN) to address the above issue. MAGNN exploits a multi-
scale pyramid network to preserve the underlying temporal
dependencies at different time scales. Since the inter-variable
dependencies may be different under distinct time scales, an
adaptive graph learning module is designed to infer the scale-
specific inter-variable dependencies without pre-defined priors.
Given the multi-scale feature representations and scale-specific
inter-variable dependencies, a multi-scale temporal graph neural
network is introduced to jointly model intra-variable dependen-
cies and inter-variable dependencies. After that, we develop a
scale-wise fusion module to effectively promote the collaboration
across different time scales, and automatically capture the im-
portance of contributed temporal patterns. Experiments on six
real-world datasets demonstrate that MAGNN outperforms the
state-of-the-art methods across various settings.
Index Terms—Multivariate time series forecasting, multi-scale
modeling, graph neural network, graph learning.
I. INTRODUCTION
Multivariate time series (MTS) are ubiquitous in various
real-world scenarios, e.g., the traffic flows in a city, the
stock prices in a stock market, and the household power
consumption in a city block [1]. MTS forecasting, which aims
at forecasting the future trends based on a group of historical
observed time series, has been widely studied in recent years.
It is of great importance in a wide range of applications, e.g.,
a better driving route can be planned in advance based on
the forecasted traffic flows, and an investment strategy can be
designed with the forecasting of the near-future stock market
[2]–[5].
Making accurate MTS forecasting is a challenging task, as
both intra-variable dependencies (i.e., the temporal dependen-
cies within one time series) and inter-variable dependencies
(i.e., the forecasting values of a single variable are affected
Ling Chen and Donghui Chen are co-first authors. Corresponding author:
Ling Chen.
Ling Chen, Donghui Chen, Zongjiang Shang, and Binqing Wu are with
the College of Computer Science and Technology, Zhejiang University,
Hangzhou 310027, China (e-mail: {lingchen, chendonghui, zongjiangshang,
binqingwu}@cs.zju.edu.cn).
Cen Zheng, Bo Wen, and Wei Zhang are with Alibaba Group, Hangzhou
311100, China (e-mail: {mingyan.zc, wenbo.wb, zwei}@alibaba-inc.com).
by other variables) need to be considered jointly. To solve
this problem, traditional methods [6]–[8], e.g., vector auto-
regression (VAR), temporal regularized matrix factorization
(TRMF), vector auto-regression moving average (VARMA),
and gaussian process (GP), often rely on the strict stationary
assumption and cannot capture the non-linear dependencies
among variables. Deep neural networks have shown superior-
ity on modeling non-stationary and non-linear dependencies.
Particularly, two variants of recurrent neural network (RNNs)
[9], namely the long-short term memory (LSTM) and the gated
recurrent unit (GRU), and temporal convolutional networks
(TCNs) [10] have significantly achieved impressive perfor-
mance in time series modeling. To capture both long-term and
short-term temporal dependencies, existing works [3], [11]–
[14] introduce several strategies, e.g., skip-connection, atten-
tion mechanism, and memory-based network. These works
focus on modeling temporal dependencies, and process the
MTS input as vectors and assume that the forecasting values
of a single variable are affected by all other variables, which
is unreasonable and hard to meet in realistic applications. For
example, the traffic flows of a street are largely affected by
its neighboring streets, while the impact from distant streets
is relatively small. Thus, it is crucial to model the pairwise
inter-variable dependencies explicitly.
Graph is an abstract data type representing relations between
nodes. Graph neural networks (GNNs) [15], [16], which can
effectively capture nodes’ high-level representations while
exploiting pairwise dependencies, have been considered as a
promising way to handle graph data. MTS forecasting can be
considered from the perspective of graph modeling. The vari-
ables in MTS can be regarded as the nodes in a graph, while
the pairwise inter-variable dependencies as edges. Recently,
several works [17]–[19] exploit GNNs to model MTS taking
advantage of the rich structural information (i.e., featured
nodes and weighted edges) of a graph. These works stack GNN
and temporal convolution modules to learn temporal patterns,
and have achieved promising results. Nevertheless, there are
still two important aspects neglected in above works.
First, existing works only consider temporal dependencies
on a single time scale, which may not properly reflect the
variations in many real-world scenarios. In fact, the temporal
patterns hidden in real-world MTS are much more compli-
cated, including daily, weekly, monthly, and other specific
periodic patterns. For example, Fig. 1 shows the power con-
sumptions of 4 households within two weeks. There exists
a mixture of short-term and long-term repeating patterns (i.e.,
daily and weekly). These multi-scale temporal patterns provide
abundant information to model MTS. Furthermore, if the
arXiv:2201.04828v2 [cs.LG] 9 Apr 2023
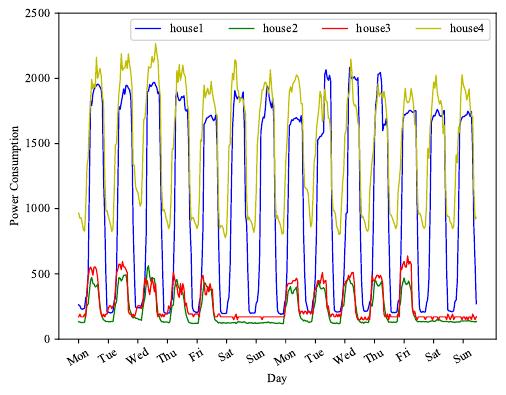
2
Fig. 1. The power consumptions of 4 households within two weeks (from
Monday 00:00 to Sunday 24:00). Households 1 and 4 have both daily and
weekly repeating patterns, while households 2 and 3 have weekly repeating
patterns.
temporal patterns are learned from different time scales sep-
arately, and are then straightforwardly concatenated to obtain
the final representation, the model is failed to capture cross-
scale relationships and cannot focus on contributed temporal
patterns. Thus, an accurate MTS forecasting model should
learn a feature representation that can comprehensively reflect
all kinds of multi-scale temporal patterns.
Second, existing works learn a shared adjacent matrix to
represent the rich inter-variable dependencies, which makes
the models be biased to learn one type of prominent and shared
temporal patterns. In fact, different kinds of temporal patterns
are often affected by different inter-variable dependencies,
and we should distinguish the inter-variable dependencies
when modeling distinct temporal patterns. For example, when
modeling the short-term patterns of the power consumptions of
a household, it might be essential to pay more attention to the
power consumptions of its neighbors. Because the dynamics of
short-term patterns are often affected by a common event, e.g.,
a transmission line fault decreases the power consumptions of
a street block, and a sudden cold weather increases the power
consumptions. When modeling the long-term patterns of the
power consumptions of a household, it might be essential to
pay more attention to the households that have similar living
habits, e.g., working and sleeping hours, as these households
would have similar daily and weekly temporal patterns. There-
fore, the complicated inter-variable dependencies need to be
fully considered when modeling these multi-scale temporal
patterns.
In this paper, we propose a general framework termed Multi-
scale Adaptive Graph Neural Network (MAGNN) for MTS
forecasting to address above issues. Specifically, we introduce
a multi-scale pyramid network to decompose the time series
with different time scales in a hierarchical way. Then, an
adaptive graph learning module is designed to automatically
infer the scale-specific graph structures in the end-to-end
framework, which can fully explore the abundant and implicit
inter-variable dependencies under different time scales. After
that, a multi-scale temporal graph neural network is incorpo-
rated into the framework to model intra-variable dependencies
and inter-variable dependencies at each time scale. Finally, a
scale-wise fusion module is designed to automatically consider
the importance of scale-specific representations and capture
the cross-scale correlations. In summary, our contributions are
as follows:
• Propose MAGNN, which learns a temporal representa-
tion that can comprehensively reflect both multi-scale
temporal patterns and the scale-specific inter-variable
dependencies.
• Design an adaptive graph learning module to explore the
abundant and implicit inter-variable dependencies under
different time scales, and a scale-wise fusion module
to promote the collaboration across these scale-specific
temporal representations and automatically capture the
importance of contributed temporal patterns.
• Conduct extensive experiments on six real-world MTS
benchmark datasets. The experiment results demonstrate
that the performance of our method is better than that of
the state-of-the-art methods.
The remainder of this paper is organized as follows: Section
II and Section III give a survey of related work and prelim-
inaries. Section IV describes the proposed MAGNN method.
Section V presents the experimental results and Section VI
concludes the paper.
II. RELATED WORK
We briefly review the related work from two aspects: the
MTS forecasting and graph learning for MTS.
A. MTS Forecasting
The problem of time series forecasting has been studied for
decades. One of the most prominent traditional methods used
for time series forecasting is the auto-regressive integrated
moving average (ARIMA) model, because of its statistical
properties and the flexibility on integrating several linear
models, including auto-regression (AR), moving average, and
auto-regressive moving average. However, limited by the high
computational complexity, ARIMA is infeasible to model
MTS. Vector auto-regression (VAR) and vector auto-regression
moving average (VARMA) are the extension of AR and
ARIMA, respectively, that can model MTS. Gaussian process
(GP) [6] is a Bayesian method to model distributions over a
continuous domain of functions. GP can be used as a prior over
the function space in Bayesian inference and has been applied
to MTS forecasting. However, these works often rely on the
strict stationary assumption and cannot capture the non-linear
dependencies among variables.
Recently, deep learning-based methods have shown su-
perior capability on capturing non-stationary and non-linear
dependencies. Most of existing works rely on LSTM and
GRU to capture temporal dependencies [20]. Compared with
RNN-based approaches, dilated 1D convolutions [18], [21] are
able to handle long-range sequences. However, the dilation
of 14
免费下载
【版权声明】本文为墨天轮用户原创内容,转载时必须标注文档的来源(墨天轮),文档链接,文档作者等基本信息,否则作者和墨天轮有权追究责任。如果您发现墨天轮中有涉嫌抄袭或者侵权的内容,欢迎发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。
下载排行榜


评论