




A_Data-assisted_Algorithm_for_Truly_Grant-free_Transmissions_of_Future_mMTC.pdf
免费下载

A Data-assisted Algorithm for Truly Grant-free
Transmissions of Future mMTC
Abstract—In truly grant-free (TGF) transmissions, pilot is
crucial to fully exploit the user separation capability of spatial
domain. Based on pilots, joint active user detection and
channel estimation can be done. The state-of-art work suggests
to use the recovered data to improve the channel estimation
accuracy. In this paper, a novel data-assisted algorithm is
proposed. This algorithm jointly utilizes the recovered and
unrecovered data to further improve the performance. The
constant modulus (CM) feature is used as the optimization
target. To obtain an efficient convergence, a fixed modulus
version of CM is employed, and multiple relatively good
spatial combining vectors are normalized and used as the
initial values of the quasi-Newton iterations. Furthermore, a
target function of post signal to interference plus noise ratio is
proposed to gain a better performance and faster convergence.
The simulation results show that the proposed method
achieves a tremendous performance gain, especially when
more receiving antennas are employed.
Keywords—Data-assisted, truly grant-free, compressed
sensing, active user detection, independent multi-pilot, mMTC
I. INTRODUCTION
Massive machine type communications (mMTC) is an
important and promising scenario in B5G and 6G [1]. Unlike
human communications, the main task of mMTC is to
support uplink sporadic small packet transmissions from a
large number of potential users. As the packet is usually
short in mMTC, the scheduling overhead in grant-based
transmission becomes very inefficient, and therefore, grant-
free, or random access, is required [2] [3].
One classical grant-free technology is semi-persistent
scheduling (SPS) [4]. SPS is used for periodic transmission
in a relatively static scenario. It is not flexible for various
kinds of mMTC services, and truly grant-free (TGF), or
autonomous grant-free [5], is suggested to solve this problem.
Different from the grant-free with pre-configurations, TGF
allows users to transmit via random resources without any
coordination. It is also described as uncoordinated multiple
access, or unsourced multiple access. TGF has two different
packet structures: data-only [5] [6] and pilot-assisted [7] [8].
In data-only schemes, the active user transmits only data. At
the receiver side, a low-complexity blind detection receiver
using the prior knowledge of data symbols is employed to
demodulate the data-only packets. Using data information,
the receiver can implement code domain user detection,
blind equalization, blind time and frequency offset
correction, and stream sorting. Blind spatial combining can
also be used when the receive antenna array is small-scale,
however, it is hard to fully utilize the user separation
capability in the spatial domain via only data. There is a
trade-off between spectrum efficiency and spatial domain
utilization to decide whether to use data-only or pilot-
assisted scheme. When the pilot overhead is small relatively
to the data packet, and the degree of freedom in spatial
domain is high, pilot-assisted method can achieve a better
overall performance.
In TGF schemes, pilot-assisted transmissions can be
realized using compressed sensing (CS) based active user
detection (AUD). Non-orthogonal pilots (NOP) are used, and
the matrix made up of all potential pilot vectors is the
sensing matrix. As the transmission is sporadic, only a small
fraction of pilots are used by the active users, which brings
about the sparsity. Using CS-AUD, the channel information
can also be estimated. It can be realized by some low
complexity iterative methods like approximate message
passing (AMP) [9], orthogonal match pursuit (OMP) [10]
and subspace pursuit (SP) [11]. Apart from pilots, data can
also be used, which provides extra information to the
classical CS model. For example, the channel estimation can
be more accurate using recovered [5], which can be
combined with existing CS methods to achieve a better
performance [8]. Using this accurate estimated channel
information, successive interference cancellation (SIC) can
be done for both recovered data and pilots. After SIC, a new
round of CS-AUD and demodulation is started. Note the
current CS-AUD schemes usually allocate different NOP for
each user to simplify the problem, but it is not practical for
such a large number of mMTC users especially when the
mobility is considered. Therefore, this paper considers a
TGF setting where every user randomly selects the pilot, and
the contribution of this paper can also be applied to those
configured settings. TGF leads to random pilot collision, but
the pilot collision probability can be low with a large number
of NOP. Similarly, independent multi-pilot (IMP) [12] can
also be used to reduce the pilot collision probability.
Different from the conventional multi-pilot scheme [13],
IMP employs iterative detection of every single pilot and
does not require the low channel correlation among users.
This paper proposes a novel scheme to utilize the
statistical information of unrecovered data to improve the
grant-free performance. The data feature of constant
modulus (CM) [14] can be used in TGF scheme, and post
signal to interference plus noise ratio (pSINR) is then
proposed to further improve the performance. Multiple
spatial combining coefficient vectors obtained from pilots
are normalized by the dispersion factor and then used as the
initial values of fixed modulus optimization. By this means,
the convergence speed is fast. The simulation results show
the proposed data-assisted algorithms perform much better
than the state-of-art work [8] using joint AUD, channel
estimation and data recovery, which is denoted by CS plus
SIC in this paper for simplicity. The contributions of this
paper are summarized as follows. (1) This paper first jointly
utilizes the statistical information of unrecovered data and
recovered data. (2) This paper employs a quasi-Newton
solver to find the local minimums close to multiple relatively
good vectors from channel estimation, which provides both
good performance and fast convergence. (3) This paper
Yihua Ma, Zhifeng Yuan, Yuzhou Hu, Weimin Li, Zhigang Li
State Key Laboratory of Mobile Network and Mobile Multimedia, ZTE Corporation, Shenzhen, China
Email:{yihua.ma, yuan.zhifeng, hu.yuzhou, li.weimin6, li.zhigang4}@zte.com.cn
978-1-7281-8298-8/20/$31.00 ©2020 IEEE
GLOBECOM 2020 - 2020 IEEE Global Communications Conference | 978-1-7281-8298-8/20/$31.00 ©2020 IEEE | DOI: 10.1109/GLOBECOM42002.2020.9348198
Authorized licensed use limited to: ZTE CORPORATION. Downloaded on April 15,2024 at 06:27:51 UTC from IEEE Xplore. Restrictions apply.
proposes a novel optimization target of pSINR, which
performs much better and converges faster than CM. (4)
This paper shows the performance can be better than the
pilot collision probability with the help of data.
The rest of this paper is organized as follows. In Section
II, CS-AUD and IMP are described. In Section III, the data-
assisted method and pSNR target function are proposed. In
Section IV, the simulation results show the tremendous
performance gain. In Section V, this paper is concluded
briefly. In this paper, (·)
-1
, (·)
T
, (·)
H
and (·)
+
denote the
inverse, the transpose, the Hermitian transpose and pseudo-
inverse of a matrix. I
M
is the identity matrix of size M×M.
II. PILOT-ASSISTED TRANSMISSION MODEL
A. General Model
In pilot-assisted transmissions, every user randomly
selects a pilot from the pilot set P = [p
1
T
, p
2
T
, ..., p
N
T
]
T
ϵ
N×L
,
where p
n
= [p
n,1
, p
n,2
, ..., p
n,L
] ϵ
1×L
, N is the number of pilots,
and L is the length of pilots. The pilot energy is normalized
as
1
1
1
2
,
L
l
ln
p
L
. Assume that the base station has M
receiving antennas, and the user has one transmitting antenna.
The pilot part of received signal from K users is
(1)
S)s(P M,LM,L
K
ki
kk
WHPWphY
where Y
P
ϵ
M×L
, h
k
ϵ
M×1
is the channel coefficient vector
of the k-th user, s(k) is the index of the pilot selected by the
k-th user, H = [h
1
, h
2
, ..., h
K
] ϵ
M×K
, P
S
= [p
s(1)
T
, p
s(2)
T
, ...,
p
s(K)
T
]
T
ϵ
K×L
, and W
x,y
denotes the complex Gaussian noise
matrix of size x×y with covariance of σ
2
. Here, a flat fading
dot-product channel model of the narrowband orthogonal
frequency division multiplexing (OFDM) system is assumed.
Similarly, the data part of received signal is
(2)
1
D M,D
K
k
M,Dkk
WHSWshY
where Y
D
= [y
d1
T
, y
d2
T
, ..., y
dM
T
]
T
ϵ
M×D
, s
i
ϵ
1×D
is the
transmit data symbol vector of the k-th user, S = [s
1
, s
2
, ..., s
K
]
ϵ
K×D
and D is the length of transmitting data symbols.
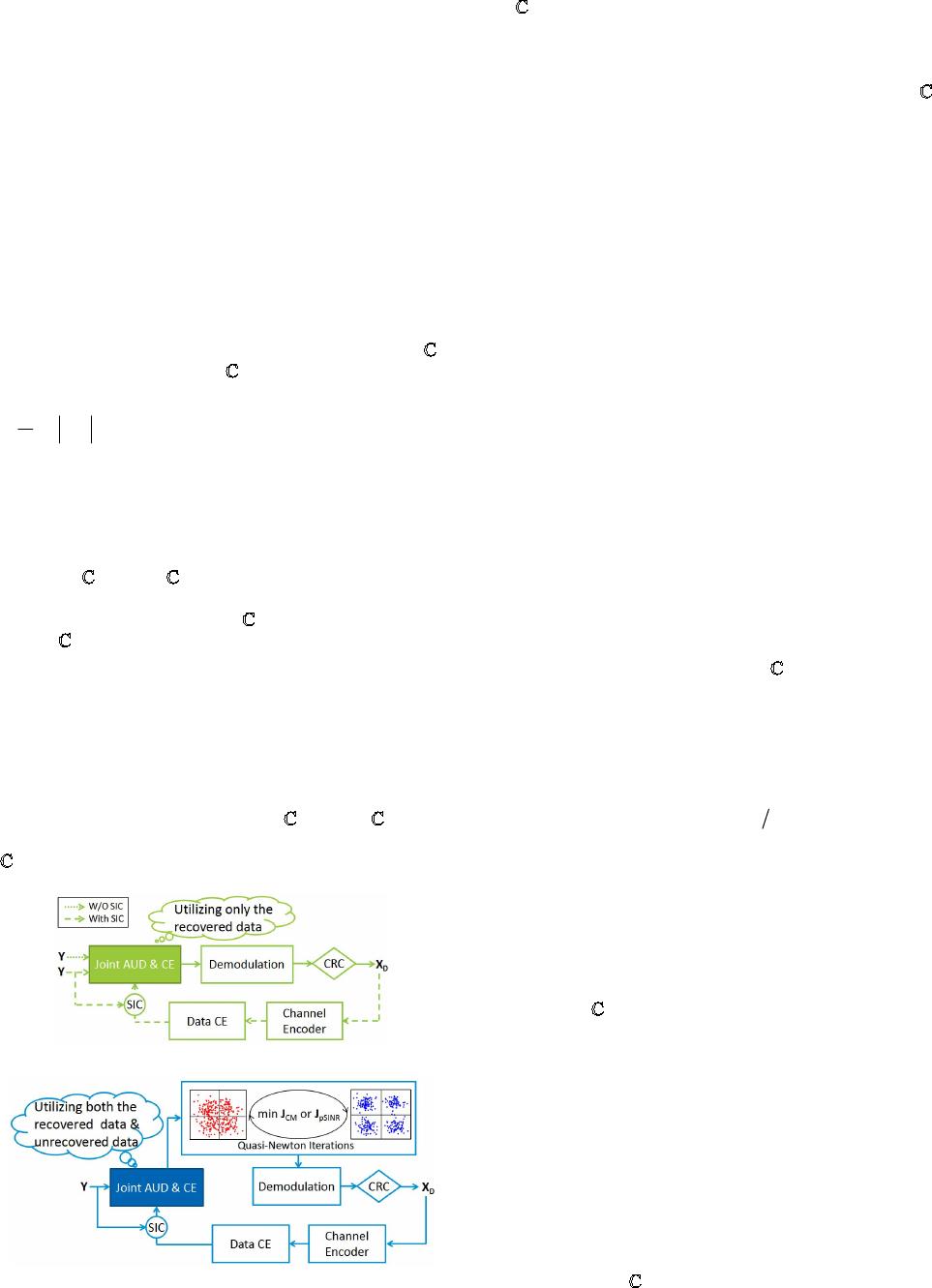
(a) The existing TGF receiver without/with SIC
(b) The proposed data-assisted TGF receiver
Fig. 1 The block diagrams of different TGF receivers. SIC is done for both
data and pilot.
Combining (1) and (2), the received signal is Y = [Y
P
, Y
D
]
ϵ
M×(L+D)
. As the receiver without SIC in Fig. 1(a), the
conventional method is to use pilot signal to do AUD and
channel estimation (CE). As the number of user is unknown
in TGF transmissions, the detected user number is K
d
. The
estimated channel matrix is Ĥ = [ĥ
1
, ĥ
2
, ..., ĥ
Kd
] ϵ
M×Kd
.
Then, the data symbol estimation using LMMSE is
(3)
ˆˆˆ
ˆ
D
1
M
2HH
YIhhhs
ki
iikk
Then, channel decoding is used to correct some error
bits. If the decoded symbols can pass the cyclic redundancy
check (CRC), the corresponding raw data is assumed to be
correctly demodulated, and the data vector is added into X
D
.
This assumption using CRC is almost exact, as the
probability of a wrong estimated data stream passing 16-bit
CRC is only 2
-16
< 1.6×10
-5
.
To support more users in TGF transmissions, SIC is
introduced to data-only [5] and pilot assisted receiver [8] as
shown in the receiver with SIC in Fig. 1(a). Note this scheme
have some different names, e.g. feedback subspace pursuit
with recovered interference cancellation [8]. In this paper, it
is named as SIC, which represents SIC utilizing recovered
data to estimate the channel and cancel both recovered data
and pilot. Apart from CS-AUD, this SIC scheme can also be
applied to IMP. They will be introduced separately.
B. Non-orthogonal Pilot
In CS-AUD, (1) is usually rewritten into
(4)
P
TTT
S
T
P L,ML,M
WHPWHPY
where H
P
= [h
p1
, h
p2
, ..., h
pN
]
T
ϵ
N×M
is the channel sum
matrix of pilots, and h
pn
is the channel sum of all users
selecting p
n
, e.g. h
pn
= 0, when there is no user selecting p
n
,
and h
pn
= h
k
, when there is only one user selecting p
n
.
In TGF, there can be more than one user selecting the
same pilot. The pilot collision probability is
(5) 111
1
K
collision
NP
It is low when the pilots number N is large, and the user
number K is small.
The channel matrix of active pilots H
A
is assumed to be
the matrix made up of all non-zero row vectors in H
P
. The
pilot-part receive signal can be written into
(6)
AAP
M,L
WPHY
where P
A
ϵ
K’×L
is made up of the active pilot vectors in P,
and K’ ≤ K is the total number of non-repetitive pilots
selected by users. Compared with the vectors in P
S
, there is
no repeated pilot vector in P
A
.
Assuming all the active pilots are detected, i.e. K
d
= K’ in
the first SIC-round, the least squares channel estimation is
(7)
ˆ
APP
PYH
After channel estimation, the spatial combining can be
done, and the signal is then decoded. If any stream passes
CRC, the corresponding raw data vector is added into the
demodulated data matrix X
D
. The corresponding codeword-
level data S
D
ϵ
Kd×D
can also be recovered. The channel
estimation of these demodulated users using data is
(8)
ˆ
H
DD
H
DDD
1
SSSYH
Authorized licensed use limited to: ZTE CORPORATION. Downloaded on April 15,2024 at 06:27:51 UTC from IEEE Xplore. Restrictions apply.
of 6
免费下载
【版权声明】本文为墨天轮用户原创内容,转载时必须标注文档的来源(墨天轮),文档链接,文档作者等基本信息,否则作者和墨天轮有权追究责任。如果您发现墨天轮中有涉嫌抄袭或者侵权的内容,欢迎发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。
下载排行榜


文档被以下合辑收录
评论