ICDE2023_Community Search A Meta-Learning Approach_腾讯云.pdf

迹部景吾

14页

0次

2025-04-21

免费下载

Community Search: A Meta-Learning Approach

Shuheng Fang

∗

, Kangfei Zhao

†

, Guanghua Li

‡

, Jeffrey Xu Yu

∗

The Chinese University of Hong Kong,

†

Beijing Institute of Technology

‡

The Hong Kong University of Science and Technology (Guangzhou)

∗

{shfang,yu}@se.cuhk.edu.hk,

†

zkf1105@gmail.com,

‡

gli945@connect.hkust-gz.edu.cn

Abstract—Community Search (CS) is one of the fundamental

graph analysis tasks, which is a building block of various real

applications. Given any query nodes, CS aims to ﬁnd cohesive

subgraphs that query nodes belong to. Recently, a large number

of CS algorithms are designed. These algorithms adopt pre-

deﬁned subgraph patterns to model the communities, which

cannot ﬁnd ground-truth communities that do not have such

pre-deﬁned patterns in real-world graphs. Thereby, machine

learning (ML) and deep learning (DL) based approaches are

proposed to capture ﬂexible community structures by learning

from ground-truth communities in a data-driven fashion. These

approaches rely on sufﬁcient training data to provide enough

generalization for ML models, however, the ground-truth cannot

be comprehensively collected beforehand.

In this paper, we study ML/DL-based approaches for CS,

under the circumstance of small training data. Instead of directly

ﬁtting the small data, we extract prior knowledge which is shared

across multiple CS tasks via learning a meta model. Each CS

task is a graph with several queries that possess corresponding

partial ground-truth. The meta model can be swiftly adapted to

a task to be predicted by feeding a few task-speciﬁc training

data. We ﬁnd that trivially applying multiple classical meta-

learning algorithms to CS suffers from problems regarding

prediction effectiveness, generalization capability and efﬁciency.

To address such problems, we propose a novel meta-learning

based framework, Conditional Graph Neural Process (CGNP),

to fulﬁll the prior extraction and adaptation procedure. A meta

CGNP model is a task-common node embedding function for

clustering, learned by metric-based graph learning, which fully

exploits the characteristics of CS. We compare CGNP with CS

algorithms and ML baselines on real graphs with ground-truth

communities. Our experiments verify that CGNP outperforms

the other native graph algorithms and ML/DL baselines 0.33

and 0.26 on F1 score by average. The source code has been

made available at https://github.com/FangShuheng/CGNP.

Index Terms—Community search, Meta-learning, Neural pro-

cess

I. INTRODUCTION

Community is a cohesive subgraph that is densely intra-

connected and loosely inter-connected in a graph. Given any

query nodes, community search (CS) aims at ﬁnding commu-

nities covering the query nodes, i.e., local query-dependent

communities, which has a wide range of real applications,

e.g., friend recommendation, advertisement in e-commence

and protein complex identiﬁcation [1], [2]. In the literature,

to model structural cohesiveness, various community models

are adopted, including k-core [3]–[5], k-truss [6], [7], k-

clique [8], [9] and k-edge connected component [10], [11].

Such models can be computed efﬁciently by CS algorithms.

But such models are designed based on some pre-deﬁned

†

Corresponding author.

MichaelaGoetz

JureLeskovec

XiaolinShi

DanielA.McFarland

RaviKumar

AndrewTomkins

JohnShawe-taylor

DeepayanChakrabarti

CarlosGuestrin

JulianMcAuley

DanielP.Huttenlocher

JonM.Kleinberg

SethA.Myers

MichaelW.Mahoney

CarolineSuen

ChantatEksombatchai

RokSosic

CristianDanescu-Niculescu-Mizil

RobertWest

ChristopherPotts

JaewonYang

DanielJurafsky

StephenGuo

MengqiuWang

JanezBrank

MyunghwanKim

LarsBackstrom

JustinCheng

JonKleinberg

ManuelGomez-Rodriguez

BernhardSchölkopf

AshtonAnderson

DanielHuttenlocher

Jr.JoséF.Rodrigues

HanghangTong

AgmaJ.M.Traina

U.Kang

MatthewHurst

SusanDumais

EricHorvitz

HimabinduLakkaraju

JureFerlez

MarkoGrobelnik

MariaCecíliaCalaniBaranauskas

PhilippeA.Palanque

JulioAbascal

SimoneDinizJunqueiraBarbosa

ManuelGomezRodriguez

JohnM.Vlissides

DouglasC.Schmidt

LadaA.Adamic

PaeaLePendu

NigamShah

SanjayRamKairam

DanJ.Wang

JeffJacobs

HeidiWang

EldarSadikov

MontserratMedina

HectorGarcia-Molina

YusukeOta

YoshihikoInagaki

KanYoneda

ShigeoHirose

NatasaMilic-Frayling

ChristinaBrandt

NadineHussami

SatishBabuKorada

RüdigerL.Urbanke

PaulBennett

LeeGiles

AlonHalevy

MartiHearst

AshwinParanjape

RobertWest0001

LeilaZia

DavidHallac

ChristopherWong

StephenBoyd

MitulTiwari

FrodeEikaSandnes

SrijanKumar

ElleryWulczyn

TimAlthoff

AustinR.Benson

BrandonNoia

ChristianReuter

JoCalder

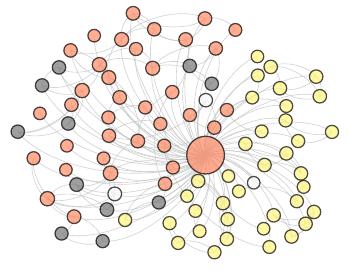
Fig. 1: An Example on DBLP: Query ‘Jure Leskovec’

community patterns which are too rigid to be used to ﬁnd

ground-truth communities in real applications. We show a

DBLP example in Fig. 1 in which nodes represent researchers

and edges represent their collaboration. The ground-truth com-

munity of ’Jure Leskovec’, i.e., the orange and white nodes

in Fig. 1 are with the researchers who have collaborations

and share the common interest of ’social networks’. Such

a community cannot be accurately found with any k-related

subgraph patterns. For example, in the community, some nodes

(e.g., Michael W. M.) have one neighbor, which can only be

found by 1-core that may result in accommodating the whole

graph.

To tackle the structural inﬂexibility of CS algorithms,

ML/DL-based solutions [12], [13] are arising as an attractive

research direction. They build ML/DL models from given

ground-truth communities and expect the models to generalize

to unknown community-member relationships. Such ML/DL-

based approaches have achieved success in ﬁnding high-

quality solutions due to two reasons. For one thing, these data-

driven approaches get rid of the inﬂexible constraints and adapt

to implicit structural patterns from data. For another thing,

the models can learn via error feedback from its predictions

on the query nodes in the ground-truth communities. But,

effective error feedback heavily relies on sufﬁcient ground-

truth communities to train, which are hard to collect and label.

On the one hand, they are labor-intensive, on the other hand,

such ground-truth communities for different query nodes can

be very different.

To deal with this problem, an effective solution is to inject

prior knowledge extracted from multiple CS tasks into the

ML model, where one CS task is a subgraph with a small

number of query nodes with partial ground-truth community

membership. The implicit prior knowledge of the CS tasks is

rather intuitive, i.e., for any query node of an arbitrary graph,

arXiv:2201.00288v3 [cs.DB] 8 Oct 2023

its communities are the nearby densely connected nodes that

share similar attributes with the query node. Such prior is

shared by different CS tasks for different query nodes in any

real-world graphs. And the prior knowledge is capable of

synthesizing similar or complementary inductive bias across

different CS tasks to compensate the insufﬁcient knowledge

from small training data, thus can be swiftly adapted to a new

task to test. In this paper, we concentrate ourselves on learning

a meta model to capture this prior by meta-learning.

There are existing meta-learning algorithms, e.g., simple

feature transfer and model-agnostic meta-learning. However,

trivial adaptations to CS tasks fail to achieve high performance

since they do not exploit the intrinsic characteristic of the

CS tasks. For CS, what a model needs to justify for each

node in a graph is whether or not it has its community

membership with any given query node. To facilitate such

binary justiﬁcation, we propose a novel model, Conditional

Graph Neural Process (CGNP), to generate node embeddings

conditioned on the small training data, where the distance

between a node embedding to that of the query node explicitly

indicates their community membership. Furthermore, as a

graph speciﬁcation of Conditional Neural Process (CNP) [14],

CGNP inherits the main ideas of CNP that implicitly learns

a kernel function between a training query node and a query

node to be predicted. In a nutshell, the learned CGNP is

not only a common embedding function but also a common

kernel function, shared across different graphs. The embedding

function transforms the nodes of each graph into a distance-

aware hidden space, while the kernel function memorizes the

small training data of each task as a hidden representation.

Compared with optimization-based meta-learning approaches

whose parameters are easy to overﬁt, the metric learning and

memorization mechanisms are more suitable for classiﬁcation

tasks with small training data, especially for imbalanced labels.

The contributions of this paper are summarized as follows:

① We formulate the problem of learning a meta model to

answer CS queries, where the meta model is to absorb the

prior knowledge from multiple CS tasks and adapt to a speciﬁc

task with only a few training data. We generalize three CS task

scenarios that represent comprehensive query cases. To the

best of our knowledge, our study is the ﬁrst attempt at meta

model/algorithm for CS. ② We explore three Graph Neural

Network based solutions, i.e., feature transfer, model-agnostic

meta-learning and Graph Prototypical Network, which are triv-

ial adaptations of existing transfer/meta-learning algorithms to

CS. We identify their individual limitations regarding predic-

tion effectiveness, generalization capability and efﬁciency. ③

We propose a novel framework, Conditional Graph Neural

Process (CGNP) on the basis of conceptual CNP and learn the

meta model in an efﬁcient, metric-based learning perspective.

We design and explore model variants with different model

complexities and different options for the core components. To

the best of our knowledge, we made the ﬁrst effort to explore

how to solve CS problem by meta-learning. ④ We conduct

extensive experiments on 6 real-world datasets with ground-

truth communities for performance evaluation. Compared with

3 CS algorithms, 4 naive approaches, and 3 supervised learning

validates our CGNP outperforms the others with small training

and prediction cost.

Roadmap: The rest of the paper is organized as follows.

section II reviews the relative work. In section III, we give

the problem statement followed by three naive solutions in-

troduced in section IV. We introduce the core idea of our

approach, CGNP in section V. We elaborate on its architecture

design and present the learning algorithms of CGNP in sec-

tion VI. We present our comprehensive experimental studies

in section VII and conclude the paper in section VIII.

II. RELATED WORK

Community Search. A comprehensive survey of CS problems

and approaches can be found in [1], [2]. In a nutshell,

CS problem can be divided into two categories. One is

non-attributed community search which only concerns the

structural cohesiveness over simple graphs and the other is

attributed community search (ACS) which concerns both the

structural cohesiveness and content overlapping or similarities

over attributed graphs. Regarding capturing the structural

cohesiveness, various community metrics have been proposed,

including k-core [3]–[5], k-truss [6], [7], k-clique [8], [9]

and k-edge connected component [10], [11]. These metrics

are inﬂexible to adapt to complex real-world graphs and

applications.

In addition to only exploiting the structural information,

ACS leverages both the structural constraint and attributes such

as keywords [15], [16], location [17], temporal [18], etc. As

two representative approaches for ACS, ATC [16] ﬁnds k-truss

community with the maximum pre-deﬁned attribute score. And

ACQ [15] ﬁnds k-core communities whose nodes share the

maximum attributes with the query attributes. Both ATC and

ACQ adopt a two-stage process. First, they ﬁnd the candidate

communities based on the structural constraints. Then, the

candidates are veriﬁed based on the computed attribute score

or the appearance of attribute set. However, the quality of the

found communities of the two approaches are unpromising

since the independent two stages fail to capture the correlations

between structures and attributes in a joint fashion.

With the development of ML/DL, recently, GNN has been

adopted for CS [12]. By recasting the community membership

determination to a classiﬁcation task, a model can learn via

its prediction error feedback given the training samples and

can adapt to a speciﬁc graph in an end-to-end way. Recently,

Gao et al. proposed ICS-GNN [12] for interactive CS, which

allows users to provide ground-truth for online incremental

learning. The model is a query-speciﬁc model that fails to

generalize to new query nodes. [13] proposes a graph neural

network based model that is trained by a collection of query

nodes with their ground-truth, and makes predictions for

unseen query nodes in a single graph.

ML/DL for Graph Analytics. Apart from CS, ML/DL

techniques are widely used in various graph analytical tasks,

including classical combinatorial optimization problems [19],

of 14

免费下载

关注

评论