




向量.doc
免费下载

授课主题 空间向量解决立体几何问题
教学目的
把立体几何问题转化为空间向量的运算问题.
教学重点
使用空间向量的方法进行空间角和距离等问题的计算
教学内容
直线与平面、平面与平面的平行与垂直的向量方法
设直线 l,m 的方向向量分别为 a=(a
1
,b
1
,c
1
),b=(a
2
,b
2
,c
2
).平面 α、β 的法向量分别
为 μ=(a
3
,b
3
,c
3
),v=(a
4
,b
4
,c
4
)(以下相同).
(1)线面平行
l∥α⇔a⊥μ⇔a·μ=0⇔a
1
a
3
+b
1
b
3
+c
1
c
3
=0.
(2)线面垂直
l⊥α⇔a∥μ⇔a=kμ⇔a
1
=ka
3
,b
1
=kb
3
,c
1
=kc
3
.
(3)面面平行
α∥β⇔μ∥v⇔μ=λv⇔a
3
=λa
4
,b
3
=λb
4
,c
3
=λc
4
.
(4)面面垂直
α⊥β⇔μ⊥ν⇔μ·v=0⇔a
3
a
4
+b
3
b
4
+c
3
c
4
=0.
空间角的计算
(1)两条异面直线所成角的求法
设直线 a,b 的方向向量为 a,b,其夹角为 θ,则
cos φ=|cos θ|=(其中 φ 为异面直线 a,b 所成的角).
(2)直线和平面所成角的求法
如图所示,设直线 l 的方向向量为 e,平面 α 的法向量为 n ,直线 l 与平面 α 所成的角为 φ,
两向量 e 与 n 的夹角为 θ,则有 sin φ=|cos θ|=.
(3)二面角的求法
①利用向量求二面角的大小,可以不作出平面角,如图所示,〈m,n〉即为所求二面角的
平面角.
②对于易于建立空间直角坐标系的几何体,求二面角的大小时,可以利用这两个平面的法
向量的夹角来求.
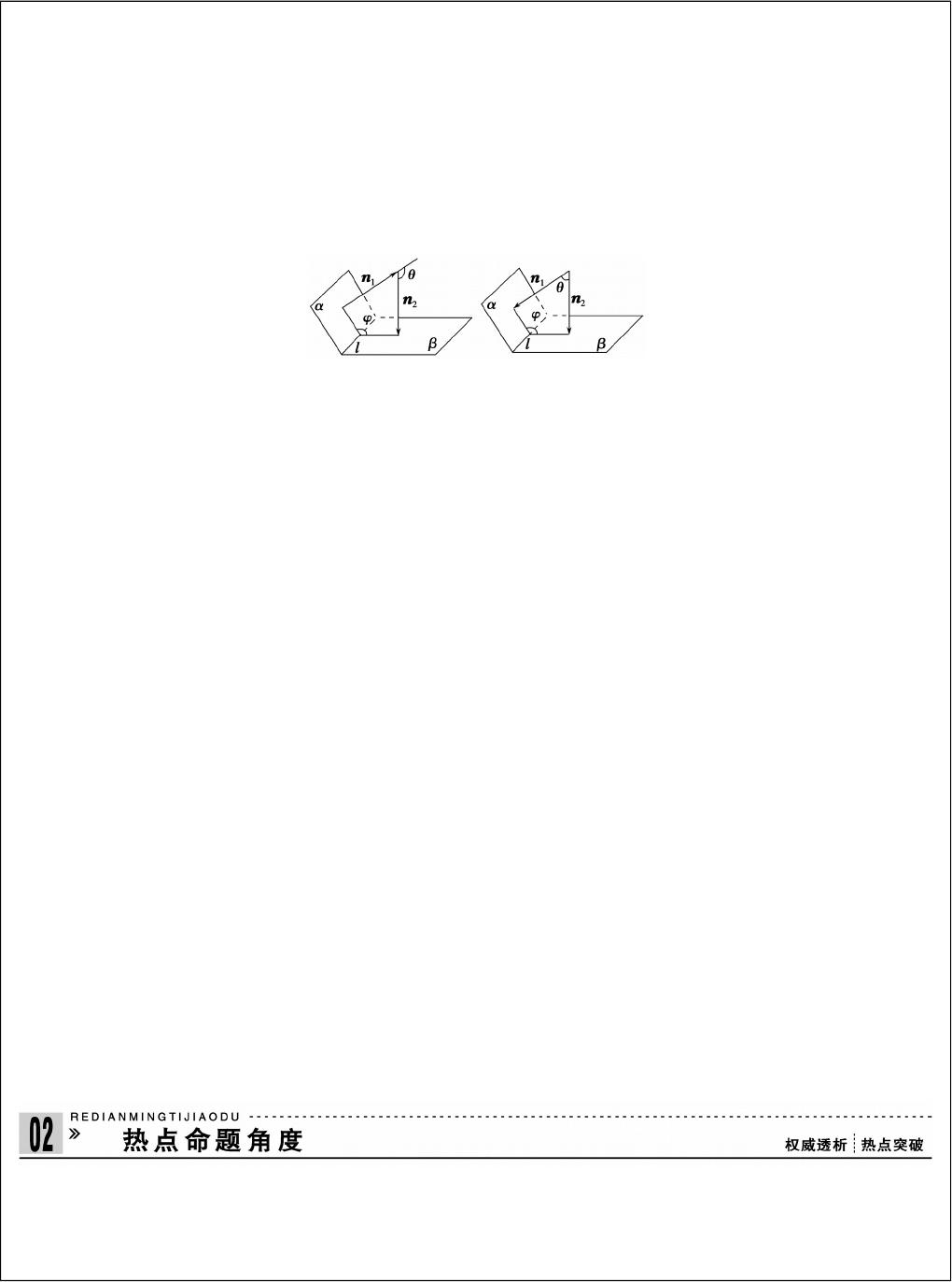
如图所示,二面角 αlβ,平面 α 的法向量为 n
1
,平面 β 的法向量为 n
2
,〈n
1
,n
2
〉=θ,则二
面有 αlβ 的大小为 θ 或 πθ.
空间距离的计算
直 线 到 平 面 的 距 离 , 两
平行平面的距离均可转化为点到平面的距离.
点 P 到平面 α 的距离,d=(其中 n 为 α 的法向量,M 为 α 内任一点).
必备方法
1.空间角的范围
(1)异面直线所成的角(θ):0<θ≤;
(2)直线与平面所成的角(θ):0≤θ≤;
(3)二面角(θ):0≤θ≤π.
2.用向量法证明平行、垂直问题的步骤:
(1)建立空间图形与空间向量的关系(可以建立空间直角坐标系,也可以不建系),用空间向
量表示问题中涉及的点、直线、平面;
(2)通过向量运算研究平行、垂直问题;
(3)根据运算结果解释相关问题.
3.空间向量求角时考生易忽视向量的夹角与所求角之间的关系:(1)求线面角时,得到的是
直线方向向量和平面法向量的夹角的余弦,而不是线面角的余弦;
(2)求二面角时,两法向量的夹角有可能是二面角的补角,要注意从图中分析
一、
多以多面体(特别是棱柱、棱锥)为载体,求证线线、线面、面面的平行或垂直,其中逻辑推
of 13
免费下载
【版权声明】本文为墨天轮用户原创内容,转载时必须标注文档的来源(墨天轮),文档链接,文档作者等基本信息,否则作者和墨天轮有权追究责任。如果您发现墨天轮中有涉嫌抄袭或者侵权的内容,欢迎发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。
下载排行榜


评论