题目描述
在有向图中,以某个节点为起始节点,从该点出发,每一步沿着图中的一条有向边行走。如果到达的节点是终点(即它没有连出的有向边),则停止。
对于一个起始节点,如果从该节点出发,无论每一步选择沿哪条有向边行走,最后必然在有限步内到达终点,则将该起始节点称作是 安全的。
返回一个由图中所有安全的起始节点组成的数组作为答案。答案数组中的元素应当按 升序 排列。
该有向图有 n 个节点,按 0 到 n - 1 编号,其中 n 是 graph 的节点数。图以下述形式给出:graph[i] 是编号 j 节点的一个列表,满足 (i, j) 是图的一条有向边。
示例 1:
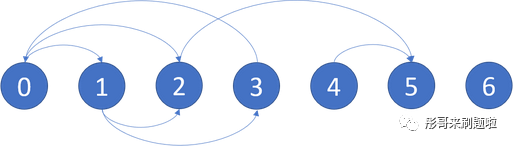
输入:graph = [[1,2],[2,3],[5],[0],[5],[],[]] 输出:[2,4,5,6] 解释:示意图如上。
示例 2:
输入:graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]] 输出:[4]
链接:https://leetcode-cn.com/problems/find-eventual-safe-states
方法一、DFS深搜
这里运用的技巧是使用一个visited数组,0表示未访问,1表示访问中,2表示访问完毕且安全的节点,如果DFS的过程中再次遇到同一个节点(即visited[i]==1),则表示这个节点是不安全的。
代码如下:
class Solution {
public List<Integer> eventualSafeNodes(int[][] graph) {
// 存储结果集
List<Integer> resultList = new ArrayList<>();
int n = graph.length;
// 0表示未访问过,1表示访问中,2表示是安全点
int[] visited = new int[n];
for (int i = 0; i < n; i++) {
// 如果从当前节点出发是安全的,则加入结果集中
if (safe(graph, i, visited)) {
resultList.add(i);
}
}
return resultList;
}
private boolean safe(int[][] graph, int index, int[] visited) {
if (visited[index] != 0) {
// 不是0,说明被访问过,判断是否为2
return visited[index] == 2;
}
// 说明未被访问过,设置为访问中
visited[index] = 1;
for (int next : graph[index]) {
// DFS过程中再次遇到相同的节点,说明有环,即为不安全,直接返回false
if (!safe(graph, next, visited)) {
return false;
}
}
// 下游节点全部遍历完成,都是安全的,说明当前节点安全,返回true
visited[index] = 2;
return true;
}
}复制
这里visited的作用有三个:1、记录DFS过程中访问过的节点;2、剪枝,防止重复访问;3、记录安全节点。
时间复杂度:O(n+m),n为节点数,m为边数。 空间复杂度:O(n),需要额外的visited数组和结果List 
方法二、拓扑排序
拓扑排序是寻找入度为0的节点,而题目给的数据是寻找最终能找到出度为0的节点,所以,我们可以用类似的思想。
我们可以按照以下步骤进行:
先整理出所有节点的出度(就是graph子数组的长度), 把出度为0的节点入队, 从队列中弹出这些节点,将入他们的那些节点的出度减一,若减到0,则把那个节点也入队 重复上述步骤,直到队列中没有元素了
因为要计算谁入了我,所以,要整理一下给定的数组,而你看到这样整理之后像是把原来的图倒过来了,所以,很多题解又叫他反图。
class Solution {
public List<Integer> eventualSafeNodes(int[][] graph) {
int n = graph.length;
// 记录每个节点的出度
int[] deg = new int[n];
// 记录谁入了我
List<List<Integer>> list = new ArrayList<>();
for (int i = 0; i < n; i++) {
list.add(new ArrayList<>());
}
// 整理数据
for (int i = 0; i < n; i++) {
deg[i] = graph[i].length;
for (int j : graph[i]) {
list.get(j).add(i);
}
}
// BFS求拓扑排序的过程(此循环可以与上面的循环合并)
Queue<Integer> queue = new LinkedList<>();
for (int i = 0; i < n; i++) {
if (deg[i] == 0) {
queue.offer(i);
}
}
// 循环找出所有符合的节点
while (!queue.isEmpty()) {
int index = queue.poll();
// 找出谁入了我,把他们的出度减一
List<Integer> whos = list.get(index);
for (Integer who : whos) {
if (--deg[who] == 0) {
queue.offer(who);
}
}
}
// 最后,deg中为0的元素就是我们要找的安全节点
List<Integer> resultList = new ArrayList<>();
for (int i = 0; i < n; i++) {
if (deg[i] == 0) {
resultList.add(i);
}
}
return resultList;
}
}复制
时间复杂度:O(n+m),n为节点数,m为边数。 空间复杂度:O(n+m),需要额外的空间存储谁入了我,也就是反向图。
虽然时间复杂度与方法一一样,但是,处理过程中使用了更多次的循环,所以,整体运行时间更慢。
结语
如果你觉得我的讲解还不错,点个赞吧。






