
本次233酱介绍下单调栈、单调队列、并查集、KMP算法,欢迎交流指正~
单调栈
「单调栈」首先是一种基于栈的数据结构,只不过通过栈来维护的是单调递增或单调递减的数据。入栈和出栈都是操作栈顶。对于每一个元素都只有一次入栈和出栈的操作,因此时间复杂度为O(N)。
递增栈(递减栈)是通过出栈的顺序是递增还是递减来定义。从栈顶到栈底是递增,则为单调递增栈;从栈顶到栈底是递减,则为单调递减栈。
假设我们把数组[7,8,3,4,1] 中的每个元素构建成一个二元组
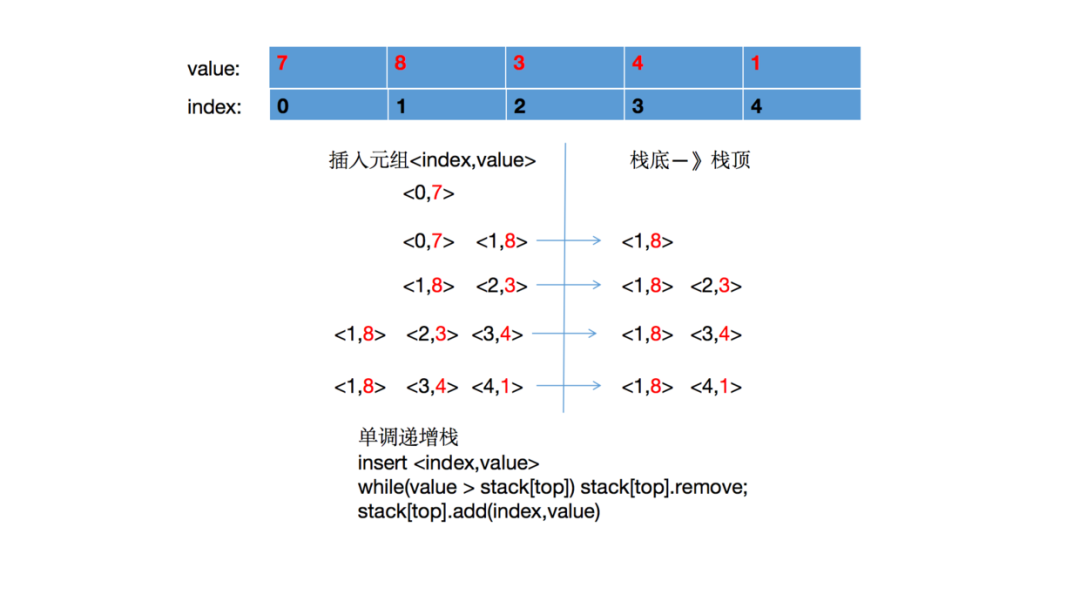
我们可以看到单调递增栈其实动态维护的是基于当前栈顶的一段单调递增区间。
那我们便可以利用栈中维护的这段单调性元素获得下一个插入元素和栈中元素的关系。如:找到从左/右遍历第一个比它大/小的元素。单调栈Java模版
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < arr.length; i++) {
//check函数:和栈的单调性定义有关
//先弹出来不符合当前遍历元素单调性的元素
while (!stack.empty() && check(stack.peek(),arr[i])) stack.pop();
//把当前遍历元素加入栈顶
stack.push(i);
}复制
我们来看一道典型的利用单调栈的问题
leetcode42:接雨水
题目描述
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

题目分析:
能够有雨水必须存在一个凹槽,即凹槽处左右两边均存在比它高的柱子。可以维护一个单调递增栈,满足栈顶的下一个元素(即左边元素)高于栈顶,当待压栈元素高于栈顶时,则栈顶元素出栈,计算栈顶所在凹槽面积后,并将待压栈元素压栈。否则,直接压栈。
leetcode42
class Solution {
public int trap(int[] height) {
Stack<Integer> stack = new Stack<>();
int res = 0;
for (int i = 0; i < height.length; i++) {
while (!stack.empty() && height[i] > height[stack.peek()]){
//凹槽下标出栈
Integer top = stack.pop();
if (stack.empty())
break;
//计算凹槽的面积
Integer left = stack.peek();
res += (Math.min(height[i],height[left]) - height[top]) * (i-left -1);
}
stack.push(i);
}
return res;
}
}复制
单调队列
「单调队列」首先是一种双端队列,然后队列中维护的元素具有单调性。其中队首元素拥有最值。从队首到对尾是递增,则为单调递增队列;从队首到对尾是递减,则为单调递减队列。
相比维护优先级队列的时间复杂度O(NlogN),维护单调队列的时间复杂度为O(N)。单调队列和单调栈比较类似,单调栈只操作栈顶。而单调队列元素从队首出最值,从队尾删除不满足单调性的元素,入满足单调性的当前入队元素。
假设我们把数组[7,8,3,4,1] 中的每个元素构建成一个二元组
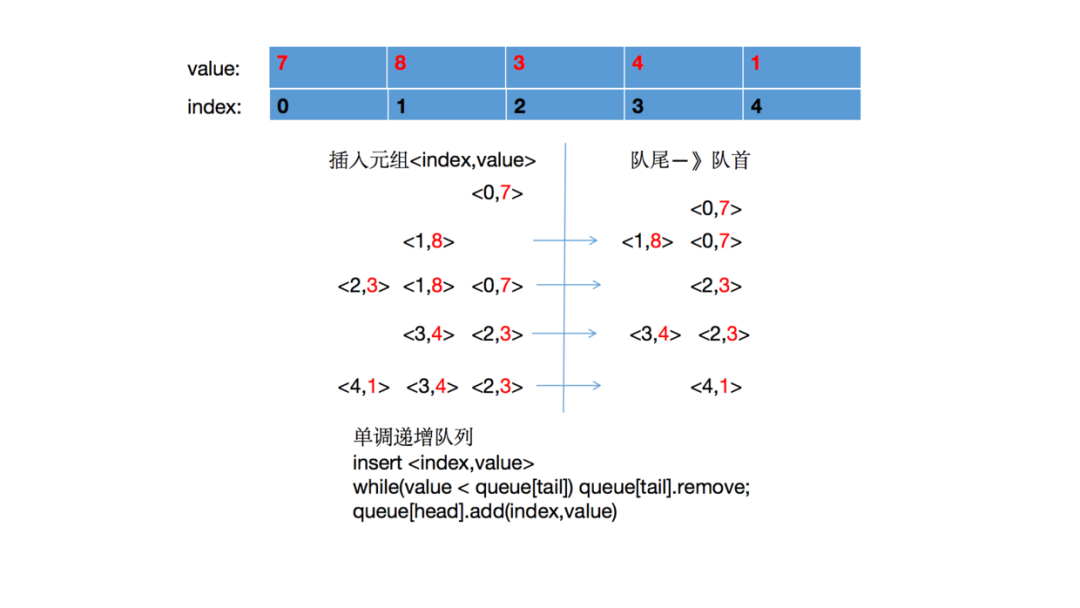
单调队列Java模版
Deque<Integer> deque = new ArrayDeque<>();
for (int i = 0; i < arr.length; i++) {
while (check(deque.getLast(),arr[i]))deque.removeLast();
while (checkout(deque.getFirst()))deque.removeFirst();
deque.addLast(i);
}复制
我们来看一道利用单调队列求区间最值的问题。
leetcode239
题目描述
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。题目示例
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释: 滑动窗口的位置最大值
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7题目分析
直接套用模版,从左到右遍历数组nums,维护一个单调递减队列。从队尾插入元素,当待插入元素>队尾元素时,队尾元素弹出,再插入待插入元素。当队列长度>k时,队首元素弹出。队首元素即为当前滑动窗口的最大值。
leetcode239
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
//实际的滑动窗口大小
int realK = k % n;
//滑动窗口的个数
int[] res;
if (realK == 0) {
realK = k;
res = new int[1];
}else
res = new int[n-realK+1];
Deque<Integer> deque = new ArrayDeque<>(realK);
int i =0;
for (int j=0 ; j < n; j++) {
while (!deque.isEmpty() && (j-deque.getFirst() >= realK)) deque.removeFirst();
while (!deque.isEmpty() && nums[deque.getLast()] < nums[j]) deque.removeLast();
deque.addLast(j);
if (j>= realK -1) {
res[i] = nums[deque.getFirst()];
i++;
}
}
return res;
}
}复制
并查集
并查集是一种树型的数据结构,用于处理一些不交集的 合并 及 查询 问题。
不交集:在数学里,若两个集合没有共同的元素,称为不交。例如{1,2,3}和{4,5,6}为不交集(disjoint sets)。
有一个联合-查找算法(union-find algorithm)定义了两个用于此数据结构的操作:
Find
:确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。Union
:将两个子集合并成同一个集合。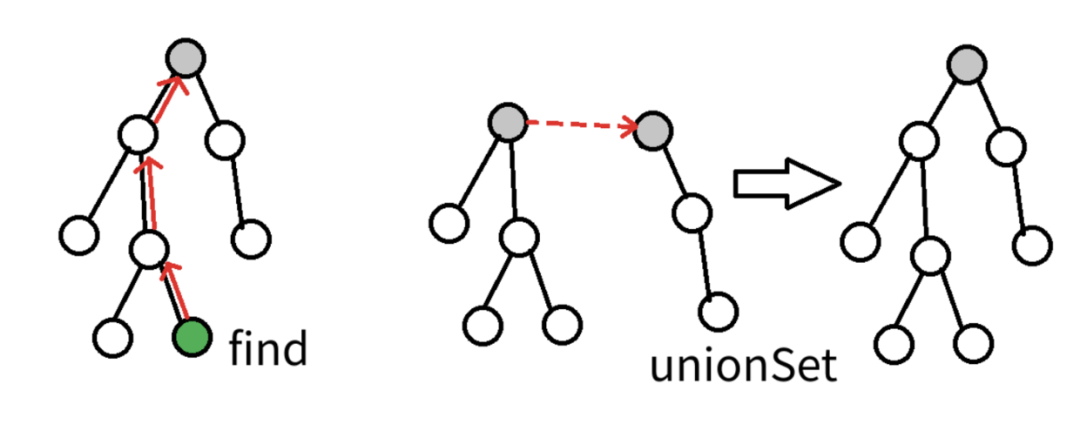
其他的重要方法,MakeSet
,用于创建单元素集合。有了这些方法,许多经典的 划分问题 可以被解决。
为了更加精确的定义这些方法,需要定义如何表示集合。一种常用的策略是为每个集合选定一个固定的元素,称为祖宗,以表示整个集合。接着,find(x)
返回x
所属集合的祖宗,而union(x,y)
使用两个集合的祖宗作为参数。并查集Java模版
public int[] makeSet(int[] arr) {
int[] parent = new int[arr.length];
for (int i = 0; i < arr.length; i++) {
parent[i] = i;
}
return parent;
}
public int find(int x){
if (parent[x] == x) {
return x;
}
return find(parent[x]);
}
public void union(int x,int y){
int rootX = find(x);
int rootY = find(y);
parent[rootX] = rootY;
}复制
如果集合的树状结构拉成了链表,则find
的效率较低。优化方式有:
路径压缩
在一个集合内,我们其实只关心每个子节点所在集合的代表是谁,并不关心它的父亲是谁。如果把在路径上的每个节点都直接连接到根上 ,则提高了find效率,这就是路径压缩。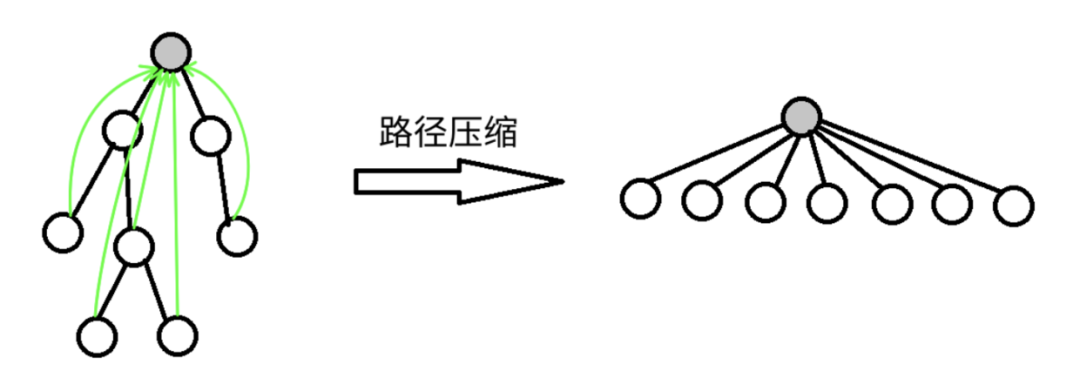
public int find(int x){
if (parent[x] == x) {
return x;
}
int rootX = find(parent[x]);
//查找x的祖先直到找到代表,于是顺手路径压缩
parent[x] = rootX;
return rootX;
}复制
关于union
,优化方式有:
按秩合并
在两个集合 A和B 合并时,选谁成为新的集合祖宗都可以得到正确结果。但是如果集合A比集合B拥有更高的深度或者子节点数目,则将集合B的祖宗作为集合A祖宗的儿子,则能使整个集合接下来执行查找操作的用时更小。
鉴于子节点数目与深度这两个特征都很容易维护,我们常常从中择一,作为估价函数。这里我们选择维护子节点数目。
int[] size = makeSet(arr);
public int[] makeSet1(int[] arr) {
int[] size = new int[arr.length];
for (int i = 0; i < arr.length; i++) {
//初始化子树的大小为 1
size[i] = 1;
}
return size;
}
public void union(int x,int y){
int rootX = find(x);
int rootY = find(y);
if (size[rootX] < size[rootY]) {
//保证小的合并到大的里
swap(rootX,rootY);
}
parent[rootY] = rootX;
size[rootX] += size[rootY];
}复制
我们来看一道经典的并差集算法题。
leetcode547: 朋友圈
题目描述
班上有 N 名学生。其中有些人是朋友,有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友,B 是 C 的朋友,那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈,是指所有朋友的集合。题目示例
输入:
[[1,1,0],
[1,1,0],
[0,0,1]]
输出:2
解释:已知学生 0 和学生 1 互为朋友,他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回 2 。题目分析
学生i和学生j互为朋友,则代表i 和 j之间有一条边,则他们应该合并到一个集合里面,因为M[i][j] 和 M[j][i] 代表一对朋友关系,所以矩阵只需要遍历一半对角线即可。求朋友圈的个数就是求不相交集合的祖宗个数(即 parent[x] = x 的个数)。
PS:我发现leetcode提交用了优化反而没有未优化的版本耗时少,那我就上传一个朴素的并差集版本吧:)
leetcode547
class Solution {
public int findCircleNum(int[][] M) {
int n = M.length;
int[] parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < i; j++) {
if (M[i][j] > 0) {
union(i,j,parent);
}
}
}
int count = 0;
for (int i = 0; i < n; i++) {
if (parent[i] == i) {
count++;
}
}
return count;
}
public int find(int x,int[] parent){
if (parent[x] == x) {
return x;
}
return find(parent[x],parent);
}
public void union(int x,int y,int[] parent){
int rootX = find(x,parent);
int rootY = find(y,parent);
parent[rootX] = rootY;
}
}复制
KMP算法
「KMP算法」是字符串查找算法,可在一个主文本字符串string
内查找一个词pattern
的出现位置。此算法通过运用对这个词在不匹配时 本身就包含足够的信息 来确定下一个匹配 将在哪里开始的发现,从而避免重新检查先前匹配的 字符。
我们先来理解下这个算法。这个算法的目标是:

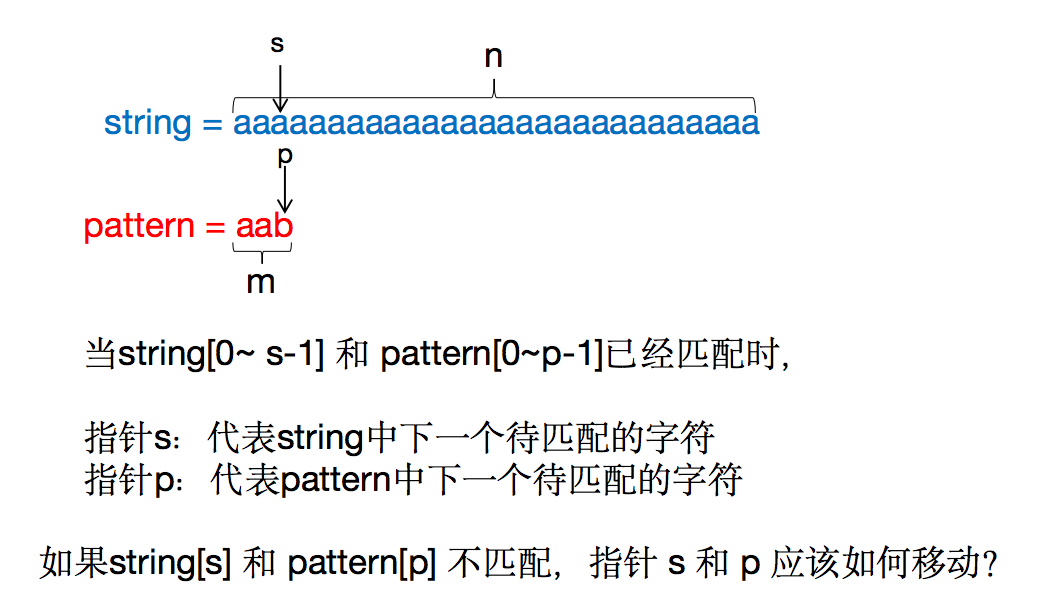
我们先来看一下简单的「从开始位置比」做法:

而KMP的做法能将时间复杂度优化到O(n+m)


那match(j)如何求呢?
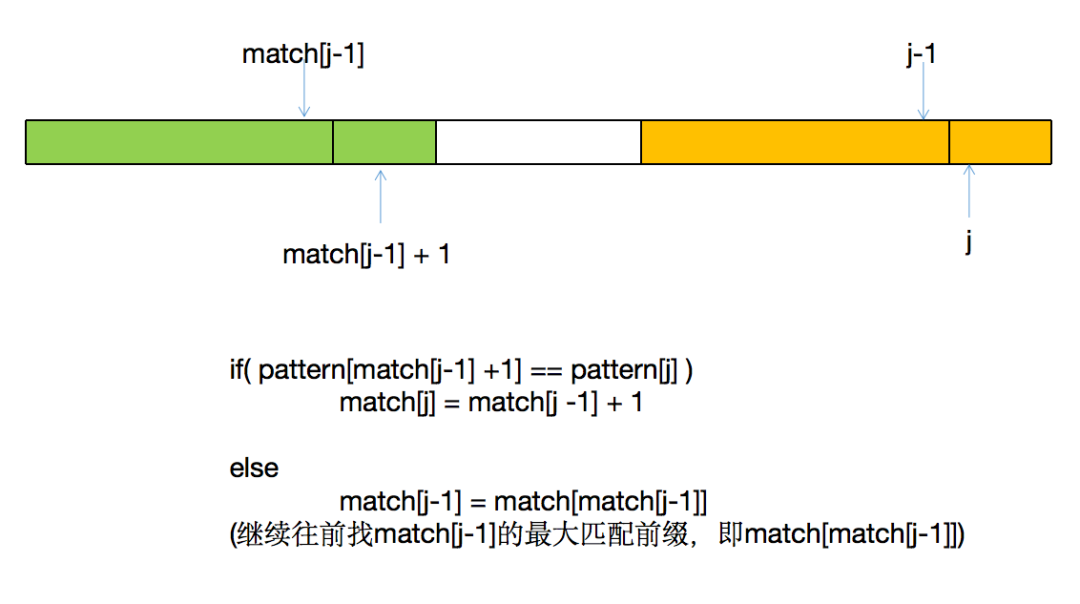
至于为什么 match[j] = match[j-1] + 1;我们可以用反证法证明一下:
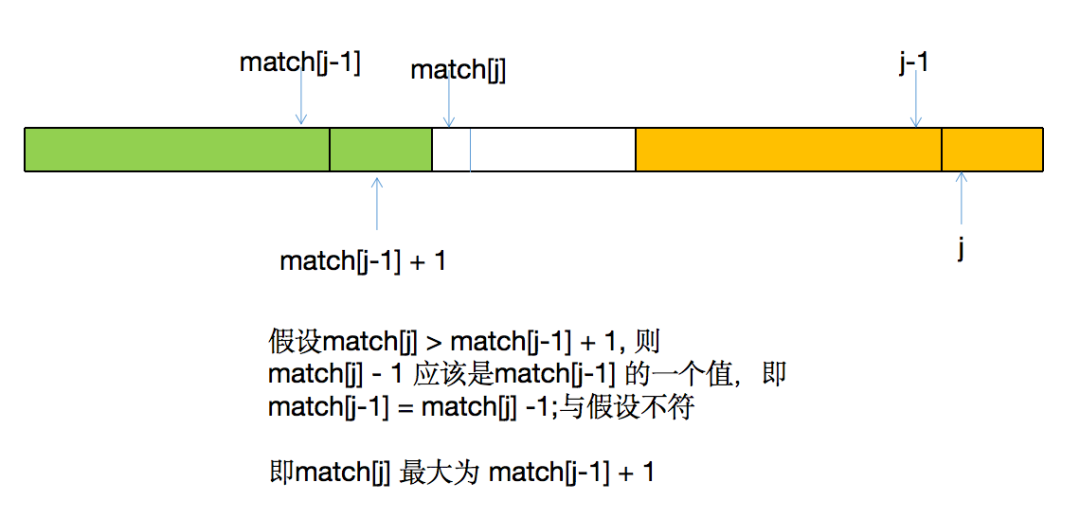
好了,关于string 和 pattern 如何确定 指针s 和 p的位置 以及 如何求match(p) 我们都分析过了,上模版吧。
KMP算法Java模版
public static int strStr(String string, String pattern) {
int m = string.length(),n=pattern.length();
//计算match(p)的值
int[] match = new int[n];
match[0] = -1;
for (int i = 1; i < n; i++) {
int j = match[i - 1];
while (j>=0 && (pattern.charAt(i) != pattern.charAt(j +1))){
j = match[j];
}
if (pattern.charAt(i) == pattern.charAt(j +1)) {
match[i] = j +1;
}else
match[i] = -1;
}
int s = 0,p=0;
//字符串string 和 pattern的匹配
while (s<m && p <n){
if (string.charAt(s) == pattern.charAt(p)) {
s++;
p++;
} else if (p>0) {
p=match[p-1] + 1;
}else s++;
}
if (p == n) {
return s-n;
}
return -1;
}
}复制
参考资料
[1].https://www.bilibili.com/video/BV1Bp411f7kZ?from=search&seid=11686356292427499857
[2].https://www.icourse163.org/learn/ZJU-93001?tid=1003997005#/learn/announce
[3].https://oi-wiki.org/ds/dsu/#_5
[4].维基百科






