
鉴于leetcode刷题即使有了思路,代码也总是磕磕绊绊调试好久,也调不对……直到发现网上不少算法模版,原来模版像单词一样,是需要背的。背会了模版也许能事半功倍。
本篇文章233酱准备了二分法、排序、位运算的一些模版,欢迎小伙伴们交流指正,持续更新中>_<
二分法
「二分查找」的思想是待搜索的数据元素满足一些二段性(前面的一半不满足这段性质,后面的一半满足这个性质,如有序数组),能够通过中间元素arr[mid]
和判断条件check(mid)
将数据分为两半,目标值target
一定在符合条件的一半中。这样通过每次折半,查找的时间的复杂为O(logN)。
假设目标值存在闭区间[l,r]中,每次将区间长度缩小一半,当l=r时,就找到了目标值target。
//区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用
public int binarySearch1(int l,int r){
while(l<r){
int mid = l +r >>1;
//如果mid满足了这个性质,target在区间[l,mid]中
if (check(mid)) r=mid;
else l = mid + 1;
}
//此时l==r,跳出后判断arr[r]是不是我们要的target即可
return r;
}
//区间[l, r]被划分成[l, mid -1]和[mid, r]时使用
public int binarySearch2(int l,int r){
while(l<r){
int mid = l + r+ 1 >>1;
//如果mid满足了这个性质,target在右区间[mid,r]中
if (check(mid)) l=mid;
else r = mid - 1;
}
//此时l==r,跳出后判断arr[r]是不是我们要的target即可
return r;
}
private boolean check(int mid) {
// mid是否满足我们区分二段性的条件
}复制
上面两段模版代码binarySearch1
和binarySearch2
微妙的区别在于mid应该被划分在区间[l,mid] 还是 区间[mid,r]。前者在满足check条件下不断向左试探target,后者在满足条件的情况下不断向右试探target。
我们通过leetcodee34 来理解这两个模版代码。
题目描述:
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
题目分析:
这道题让我们找到target的开始位置和结束位置,Step1:找开始位置
从[l,r]中找到start,不断向左试探。更新r=mid,套用模版binarySearch1
。
Step2:找结束位置
Step1结束后如果 arr[r] == target,则说明r是target的开始位置
继续二分[r,nums-1]:不断向右试探。更新l=mid,套用模版binarySearch2
完整代码为:
class Solution {
public int[] searchRange(int[] nums, int target) {
int[] result = new int[2];
result[0] = -1;
result[1] = -1;
if (nums.length == 0) {
return result;
}
int l = 0, r = nums.length - 1;
//Step1:从[l,r]中找到start,不断向左试探
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] >= target) {
r = mid;
} else {
l = mid + 1;
}
}
if (nums[r] != target) {
//不存在目标元素
return result;
}
result[0] = r;
//Step2:从[r,nums.length-1]中寻找end,不断向右试探
int L = r, R = nums.length - 1;
while (L < R) {
int mid = L + R + 1 >> 1;
if (nums[mid] == target) {
L = mid;
} else {
R = mid - 1;
}
}
result[1] = L;
return result;
}
}复制
排序算法
排序算法的复杂度图表如下:
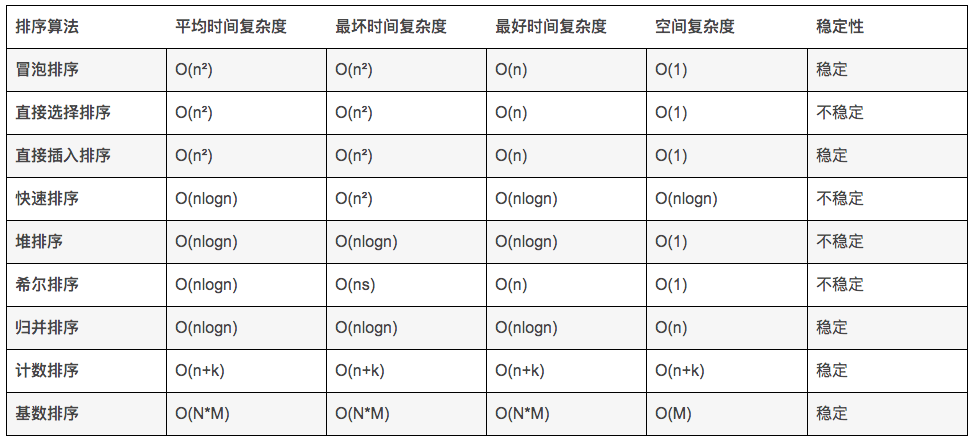
这里我准备了一下快速排序、堆排序和归并排序的模版。
快速排序和归并排序都用了分治思想,就是将一个大问题分解成小的子问题来解决。小的子问题解决了,大问题也就解决了。通过将全局排序不断分解,局限在子问题内排序,减少了排序中不必要的重复比较操作。从而使平均复杂度降为O(nlogn)。不过在全局排序的分与合的策略上,两者有一些区别。
快速排序
「快速排序」的思想是使用分治法(Divide and conquer)策略来把一个序列(list)分为较小和较大的2个子序列,然后递归地排序两个子序列。
public void quickSort(int[]nums,int l,int r){
//终止条件
if (l>=r) {
return;
}
int i = l - 1, j = r + 1, partition = nums[l + r >> 1];
while (i<j){
while (nums[ ++ i] < partition);
while (nums[ -- j] > partition);
if (i<j) {
swap(nums,i,j);
}
}
//递推步骤
//注意:分界区间是[l,j] 和 [j+1,r],因为如果r-l+1 = 偶数时,跳出循环时 i>j。此时j才是分区的位置
quickSort(nums,l,j);
quickSort(nums,j+1,r);
}
private void swap(int[]nums,int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}复制
归并排序
「归并排序」指的是将两个已经排序的序列合并成一个序列的操作。归并排序算法依赖归并操作。
public static void mergeSort(int[] nums,int l,int r){
//终止条件
if (l>=r) {
return;
}
int mid = l+r>>1;
//递推公式
mergeSort(nums,l,mid);
mergeSort(nums,mid+1,r);
//合并过程
int[] temp = new int[r-l+1];
int k =0,i=l,j=mid+1;
while (i<=mid && j <= r){
if (nums[i]<= nums[j]) {
temp[k++] = nums[i++];
}else {
temp[k++] = nums[j++];
}
}
while (i<=mid) temp[k++] = nums[i++];
while (j<=r) temp[k++] = nums[j++];
for ( i=l,j=0;i<=r;i++,j++){
nums[i] = temp[j];
}
}复制
堆排序
堆是一个近似完全二叉树的结构,并同时满足堆的性质:即子节点的键值或索引总是小于(或者大于)它的父节点。
如果先构建一个大顶堆,重复从最大堆取出数值最大的结点(把根结点和最后一个结点交换,把交换后的最后一个结点移出堆),并让残余的堆维持最大堆性质,从而完成排序。
public void heapSort(int[] nums){
//构建一个大顶堆
int lastIndex = nums.length -1;
int maxParent = (lastIndex>>1) -1;
for (int i = maxParent;i>= 0;i--){
maxHeapify(nums,i,lastIndex);
}
//不断交换数组的最后面
for(int i = lastIndex;i>0;i--){
swap(nums,0,i);
maxHeapify(nums,0,i-1);
}
}
private void maxHeapify(int[] nums,int parent,int lastIndex){
int lChild = (parent<<1)+ 1;
int rChild = lChild + 1;
if (lChild > lastIndex) {
return;
}
int maxChild = lChild;
if (rChild <= lastIndex && nums[rChild] > nums[lChild]) maxChild = rChild;
if (nums[maxChild] > nums[parent]) {
swap(nums,maxChild,parent);
//需要继续判断换下后的父节点是否符合堆的特性
maxHeapify(nums,maxChild, lastIndex);
}
}
private void swap(int[]nums,int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}复制
位运算
异或:
a=0 ^ a=a ^ 0
0=a^a
a=a ^ b ^ b交换两个数
a=a^b
b=a^b
a=a^b与运算:
求n的第k位数字: n >> k & 1移除最后一个 1
n=n&(n-1)
我们看一下leetcode191如何运用上述性质。
题目描述:计算数字的二进制中有多少个1
题目示例:
输入:00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。
方法一:常规解法,如果n & mask != 0,说明n的右边第k位为1,则计数+1,mask左移一位。
public int hammingWeight(int n) {
int bits = 0;
int mask = 1;
for (int i = 0; i < 32; i++) {
if ((n & mask) != 0) {
bits++;
}
mask <<= 1;
}
return bits;
}复制
方法二:令n=n&(n-1),如果 n!=0,则说明去掉了最右面的1,则计数+1
public int hammingWeight(int n) {
int bits =0;
while(n != 0){
bits++;
n = n&(n-1);
}
return bits;
}复制
参考资料:
[1].https://www.acwing.com/blog/content/277/
[2].https://stackoverflow.com/questions/4678333/n-n-1-what-does-this-expression-do
[3].维基百科






