原文链接:
https://medium.com/@therobbrennan/explore-openai-vector-embedding-with-neo4j-6ea2a40693d9
本文要和下附的这个 GitHub 项目配合使用哦,图中所有的代码都可以在里面找到:
https://github.com/TheRobBrennan/fixie-ai-llm-hackathon-20230916/blob/main/guides/Walkthrough.md

本文的目标是:
了解如何将数据存储为 Neo4j 向量并在轻量级检索增强生成 (RAG) 示例应用程序中使用
根据示例查询从 Wikipedia 加载源数据
处理结果并将其存储为 Neo4j Vector
探索在 Neo4j 中使用向量嵌入的示例查询和方法
初始设置
为今天的实操我们需要准备以下内容:
OpenAI API 密钥
Neo4j Aura 上的免费 Neo4j 图数据库
使用 VS Code 进行开发的本地 Python 项目
之前我们在从零开始:大模型简介与应用|实战系列中介绍过如何获得 OpenAI 的 API 密钥,有需要的可以参考,这里就不再赘述了。
Neo4j 图数据库
在本演示中,我们使用 Neo4j Aura 的免费套餐托管图数据库。
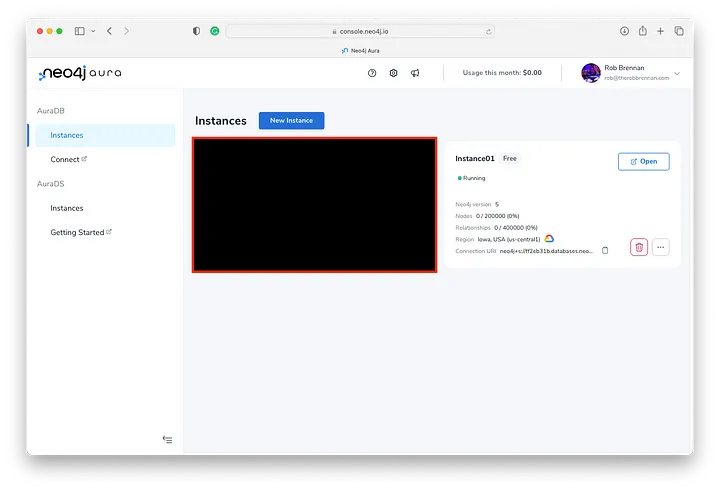
首先,我们需要单击“新建实例”:

一般来说,我们只能使用 Neo4j Aura 帐户创建一个免费套餐实例。
让我们单击“创建免费实例”开始:
我们需要立即在环境变量文件中声明多个配置设置,因此建议单击“下载”并继续将这些设置保存到计算机上的文本文件中。
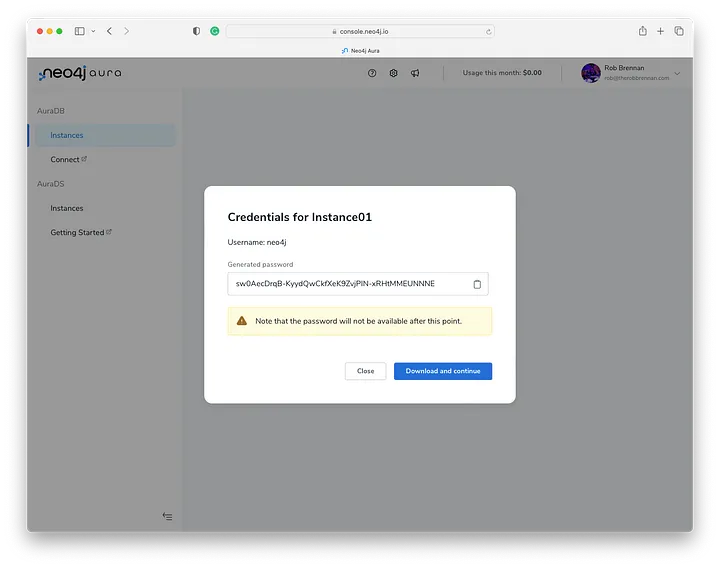
以下是从 Neo4j Aura 下载的示例配置文件,需要注意的是这个文件仅供展示,已经不可用了:
几分钟后,我们将看到我们的实例已准备好运行:
使用 VS Code 进行开发的 Python 项目
在继续操作之前,记得确保Python的版本为3.11.1或更高版本。
对于这个项目,作者创建了一个新的 GitHub 存储库
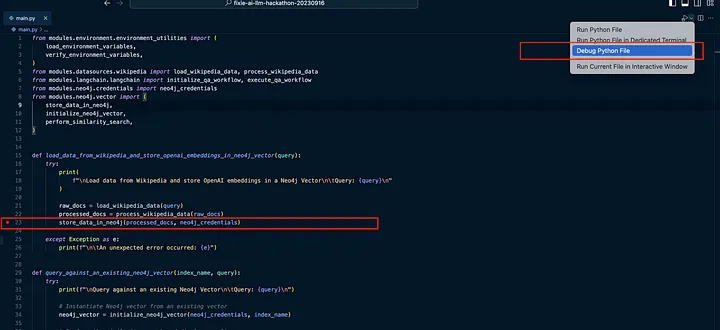
如果使用 VS Code,则可以在开发和探索代码库时使用 IDE 中的内置调试功能。如果我们加载 main.py 文件,我们可以在左侧装订线中添加一个断点(本例中的第 23 行),然后单击 Debug Python File:
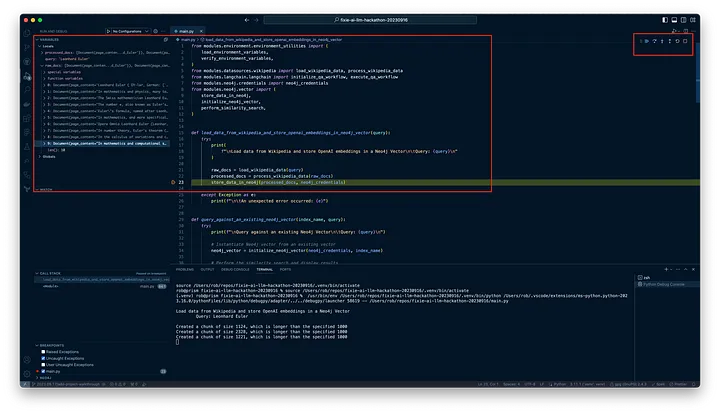
一旦到达断点,我们就会在左侧栏中看到丰富的调试信息。
剩下的就是更新我们的环境变量。请务必使用保存的相应 OpenAI API 密钥和 Neo4j 凭据打开.env.sample并将其另存为.env 。


正式开始
main.py 是我们的主脚本,它导入了作者在 ChatGPT 4 的帮助下在最终重构过程中创建的几个模块:
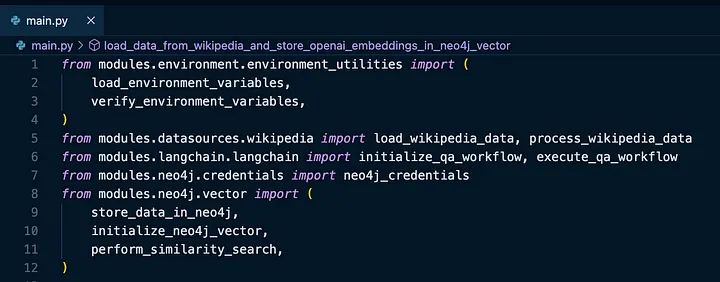
对于不熟悉 Python 的人来说,此导入模式可用于加载子目录中的文件。
例如,该项目的 ./modules/environment 目录中有一个 environment_utilities.py 文件:
我们的示例应用程序相对简单。我们将:
加载 .env 中定义的环境变量
根据初始查询从维基百科加载原始数据
处理(分块和清理)维基百科数据
使用 OpenAI 嵌入和 Neo4j Vector 在 Neo4j 中存储维基百科数据块
然后,我们将针对 Neo4j 后端提出一个问题,看看我们的数据是否按预期导入
最后,我们将使用 LangChain 和 Neo4j 后端遵循简单的问答工作流程
加载环境变量
让我们看一下
modules/environment/environment_utilities.py
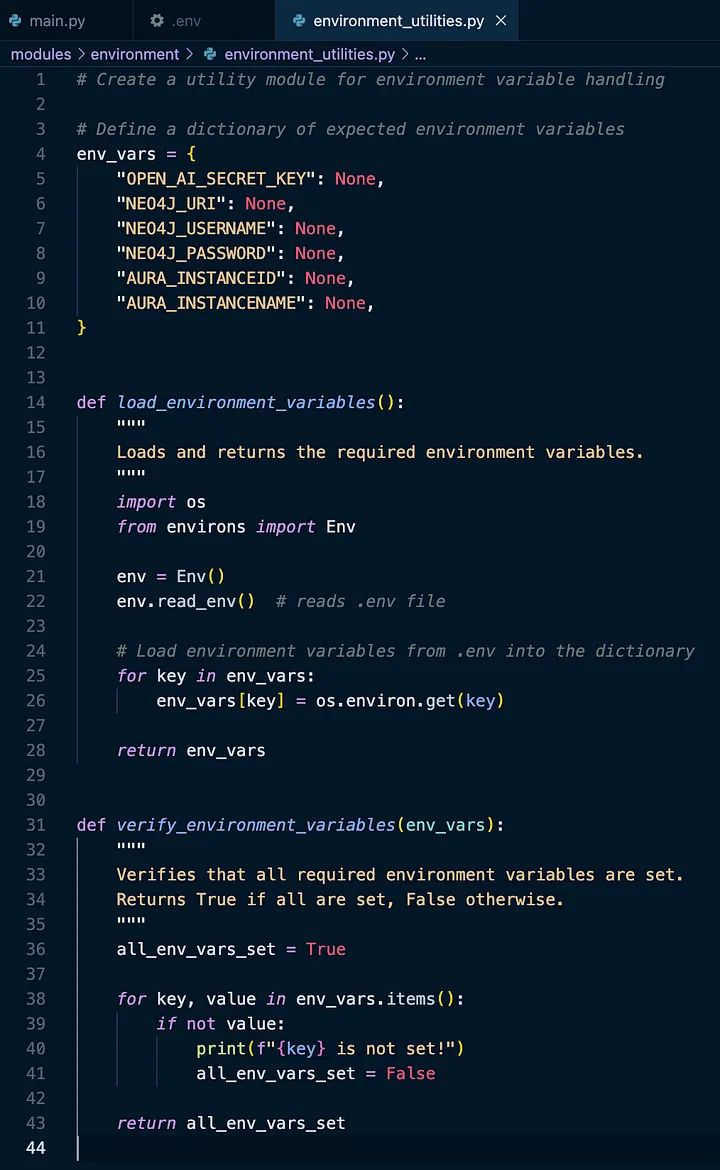
请注意以下事项:
~4 — 我们已经定义了需要为此应用程序定义的环境变量字典。
~14 — 我们有一个 load_environment_variables 函数,它将读取我们的 .env 文件
~31 — 我们有一个 verify_environment_variables 函数,它可以让我们知道是否已加载所有必需的环境变量
如果我们没有加载所有预期的环境变量,该脚本将报错并终止。
NEO4J_URI is not set!Traceback (most recent call last):File "/Users/rob/repos/fixie-ai-llm-hackathon-20230916/main.py", line 7, in <module>from modules.neo4j.credentials import neo4j_credentialsFile "/Users/rob/repos/fixie-ai-llm-hackathon-20230916/modules/neo4j/credentials.py", line 11, in <module>raise ValueError("Some environment variables are missing!")ValueError: Some environment variables are missing!复制
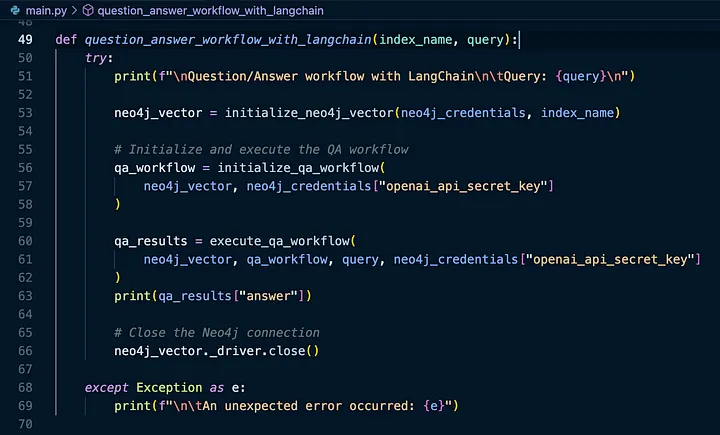
01
从 Wikipedia 加载用户查询的数据
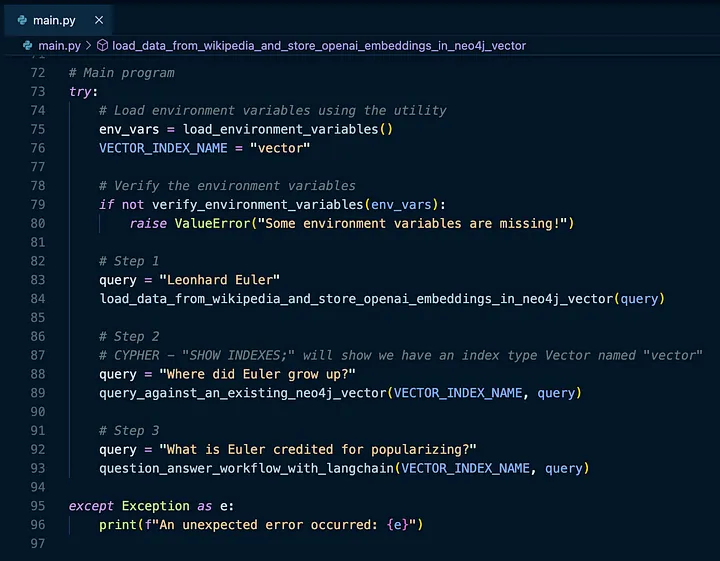
一旦我们确信已定义所有的环境变量,我们就可以深入研究这个项目的核心内容。首先看看我们可以从维基百科加载哪些关于被认为是第一个开发图论的人:Leonhard Euler 的数据。
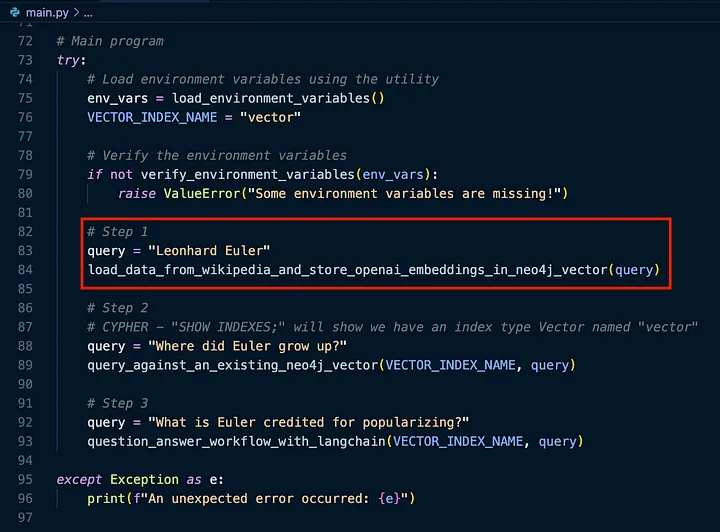
如果我们查看 main.py 文件,我们会看到顶部定义了一个函数:
load_data_from_wikipedia_and_store_openai_embeddings_in_neo4j_vector:
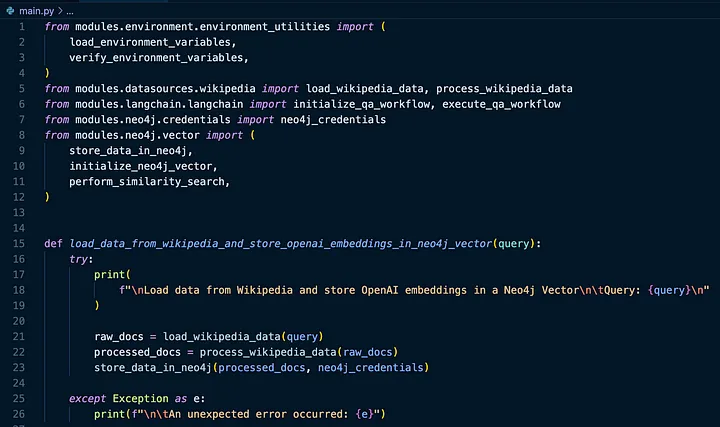
从维基百科加载原始数据
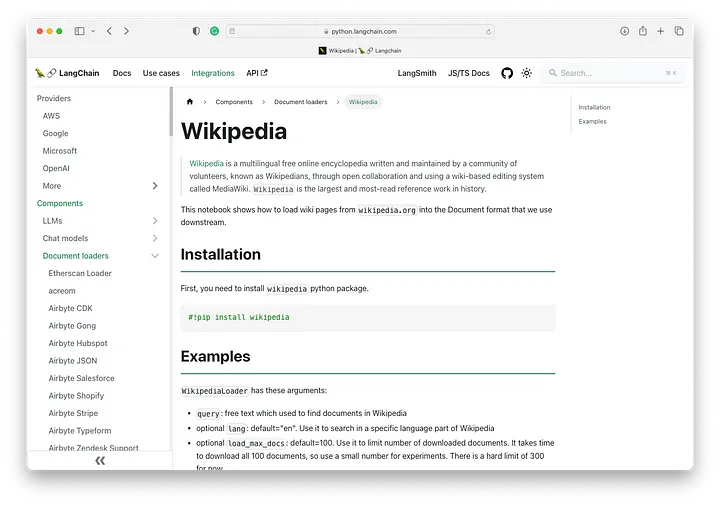
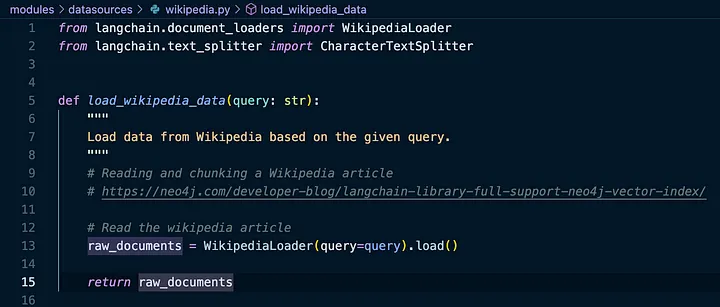
首先,使用 LangChain 的 WikipediaLoader 根据提供的查询从维基百科加载原始数据。
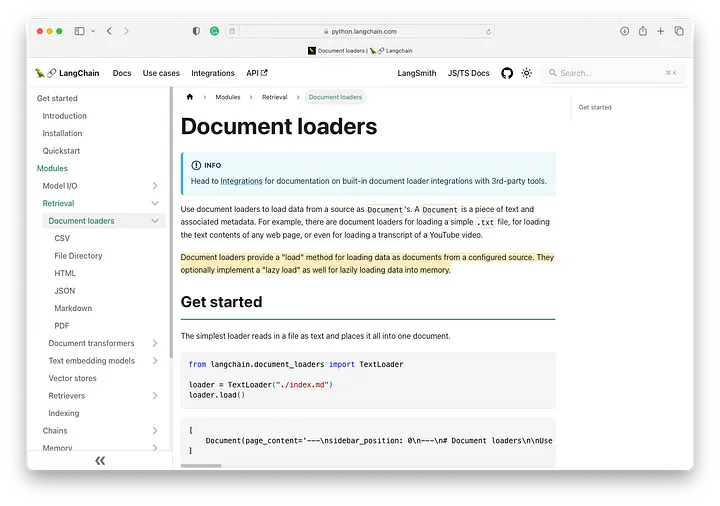
如果我们看一下左侧边栏,我们可以看到我们可以使用的 LangChain 文档加载器的度量标准。对于这个例子,我们可以看到一个可供我们使用的维基百科文档加载器。
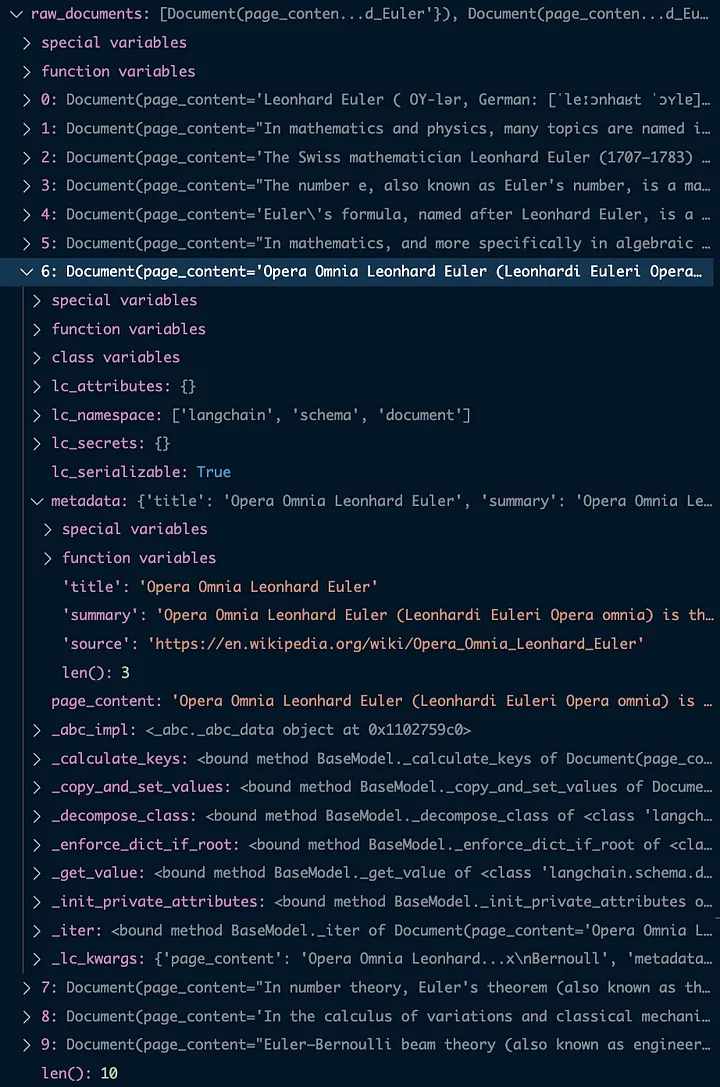
如果我们在 VS Code 中使用一些有用的调试来深入了解,我们可以看到 raw_documents 包含:
处理(分块和清理)维基百科数据
有了 raw_documents,让我们看看接下来做什么。
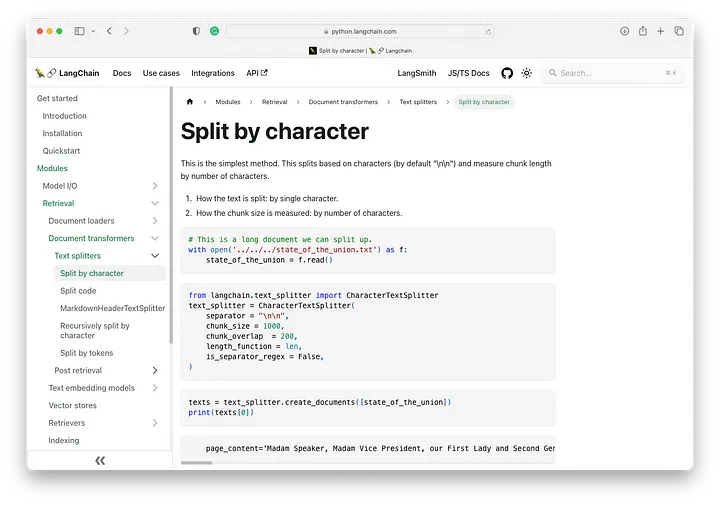
接下来,我们使用 tiktoken 文本分块模块,该模块使用 OpenAI 制作的分词器,将文章分成具有 1000 个标记的块。
让我们在我们的模块中使用 LangChain CharacterTextSplitter:
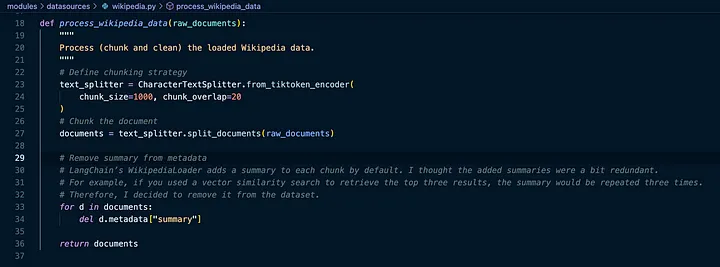
这将生成 processed_docs,然后我们可以使用它来准备将数据存储在 Neo4j 中:
使用 OpenAI 嵌入和 Neo4j Vector 存储数据块
最后将我们的 processed_docs 存储在 Neo4j 中:
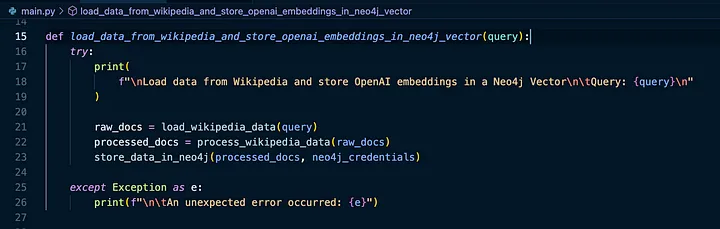
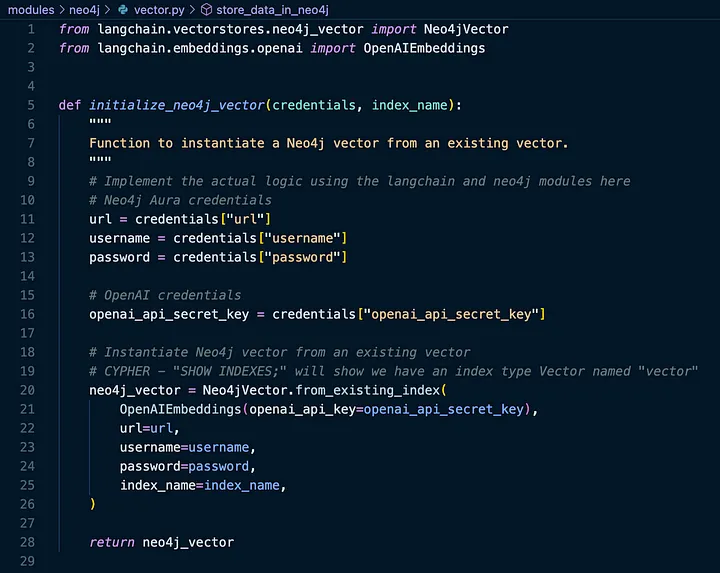
我们将从 module/neo4j/credentials.py 导入凭证以连接到 Neo4j(使用我们加载的环境变量):

我们可以注意到其中有一个open_api_secret_key。我们将使用 OpenAI 生成我们需要的向量嵌入细节,因此为了简单起见,作者将其包含在配置中。
这里有两个重要的点:
LangChain 可以轻松地将文档导入 Neo4j 并使用新添加的向量索引对其进行索引。
Neo4j 向量索引被包装为 LangChain 向量存储,因此遵循用于与其他向量数据库交互的语法。
我们来看看 LangChain Vector Stores:

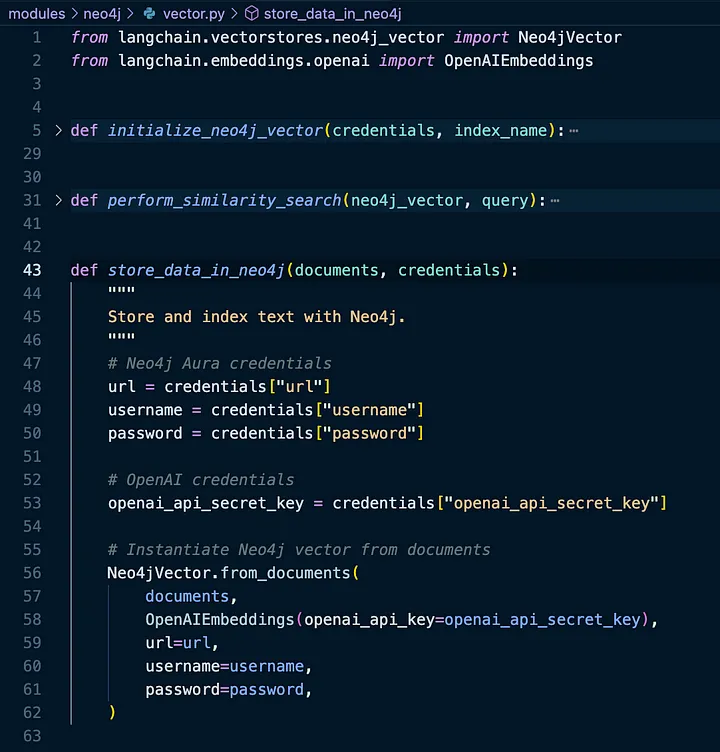
让我们看一下 modules/neo4j/vector.py,看看如何将 processed_documents 导入 Neo4j 并通过 store_data_in_neo4j 函数使用新添加的向量索引对它们进行索引:
在我们完整执行 main.py 脚本之前,请查看 Neo4j Aura 中的 Neo4j 图形数据库。单击显示实例的卡右上角的“打开” 。

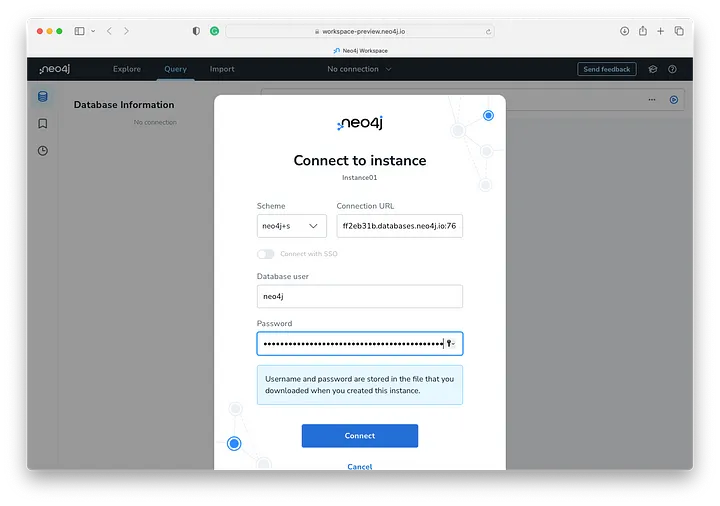
这是 Neo4j 工作区。我们将使用它来探索、查询并与我们的图数据库交互。
运行脚本
# Create a new virtual environment for the project% python3 -m venv .venv# Activate your virtual environment% source .venv/bin/activate(.venv) %# Install the packages from requirements.txt(.venv) % pip install -r requirements.txt# Copy the sample environment variables file to .env(.venv) % cp .env.sample .env# Update .env with your OpenAI API key and Neo4j credentials# Load your environment variables (defined in ".env")(.venv) % source .env# Run the main script (~30 seconds or more to complete)(.venv) % python3 main.py## OPTIONAL: Use time to track the execution of your script(.venv) % time python3 main.py: : : : : : : : : : : : : : : :python3 main.py 2.98s user 2.20s system 13% cpu 39.288 total复制
运行脚本后,单击上次更新时间附近的刷新符号:
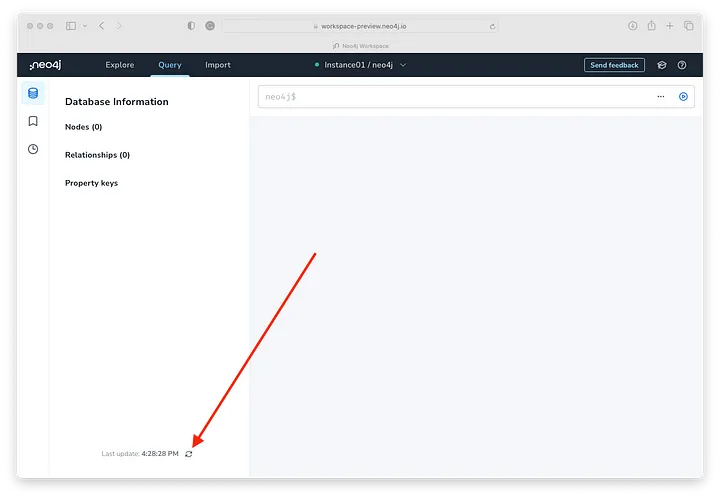
可以看到我们的图数据库有一些数据,我们可以看到有二十一 (21)个块节点 - 具有各种可用的属性键:
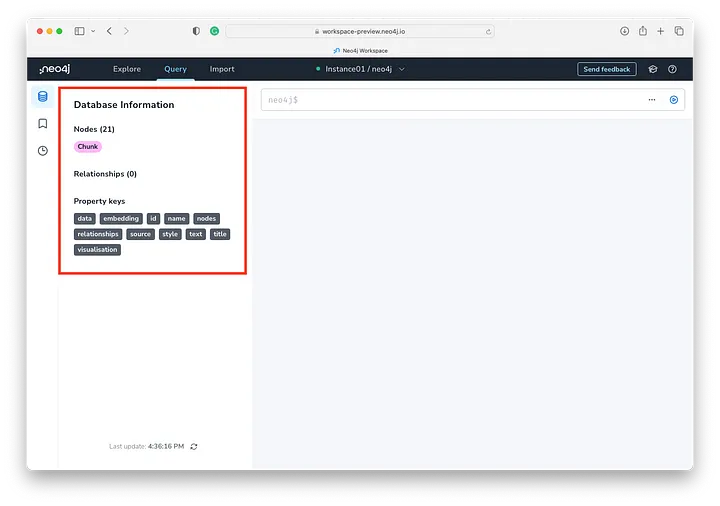
如果是第一次使用 Neo4j,请不用担心。我们将仅仅触及表面来看看我们导入了哪些数据。
如果我们查看使用 Cypher 查询 Neo4j 数据库指南,我们可以看到 Neo4j 使用 Cypher 作为查询图的语言。
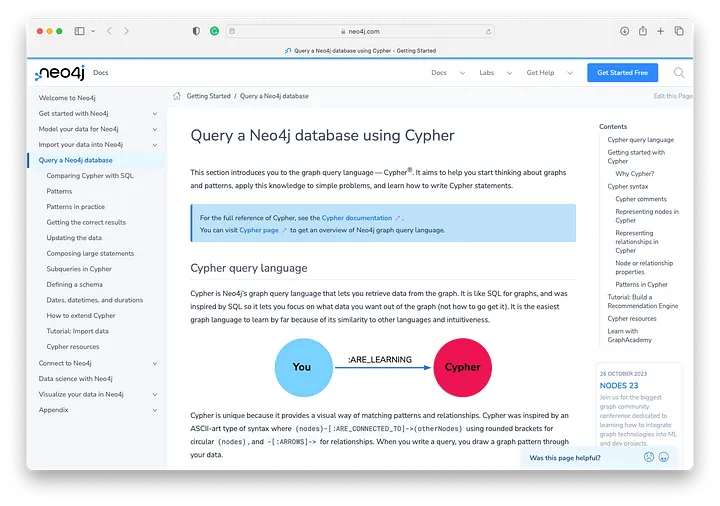
我们将创建一个简单的 Cypher 查询,它将匹配图中的所有节点(引用为变量 n)并显示结果:
MATCH (n) RETURN n复制
这将向我们展示如下内容:
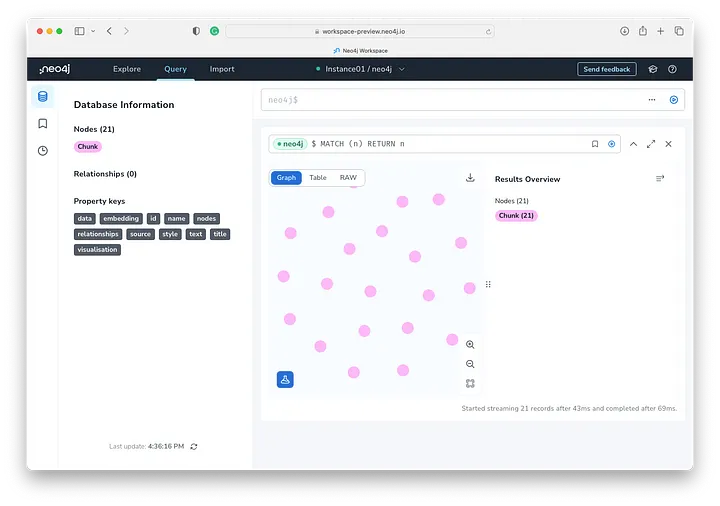
这个图表视图很有趣,有很多彩色节点,并在高级别显示块标签。让我们放大一下。
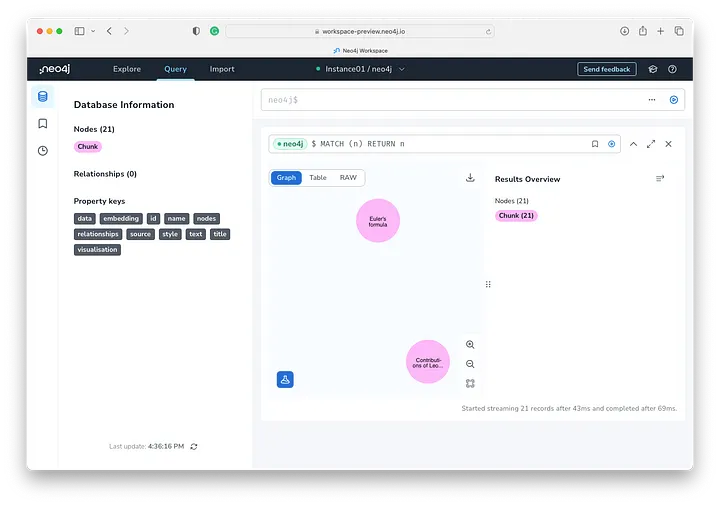
我们可以看到标题为 Euler's Formula 的 Chunk 节点,该节点表示包含在 text 属性中的文本块以及存储在 embedding 中的 OpenAI 嵌入。
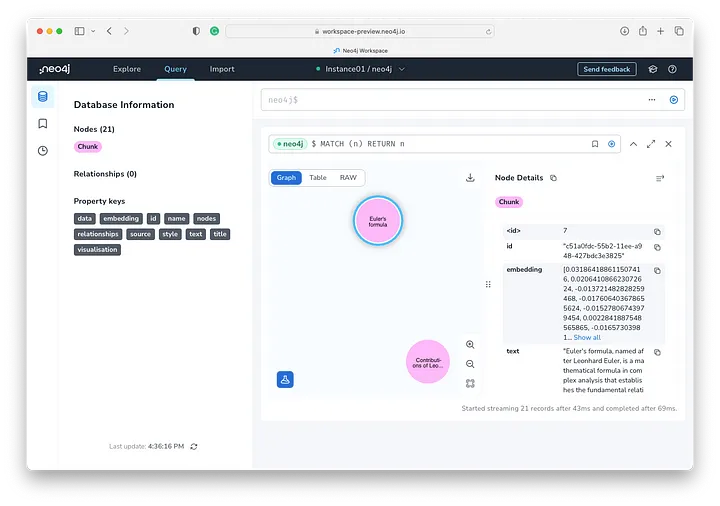
除了作为众多 LangChain 文本嵌入模型之一之外,还包含 LangChain OpenAIEmbedding 模型以及这些嵌入值。
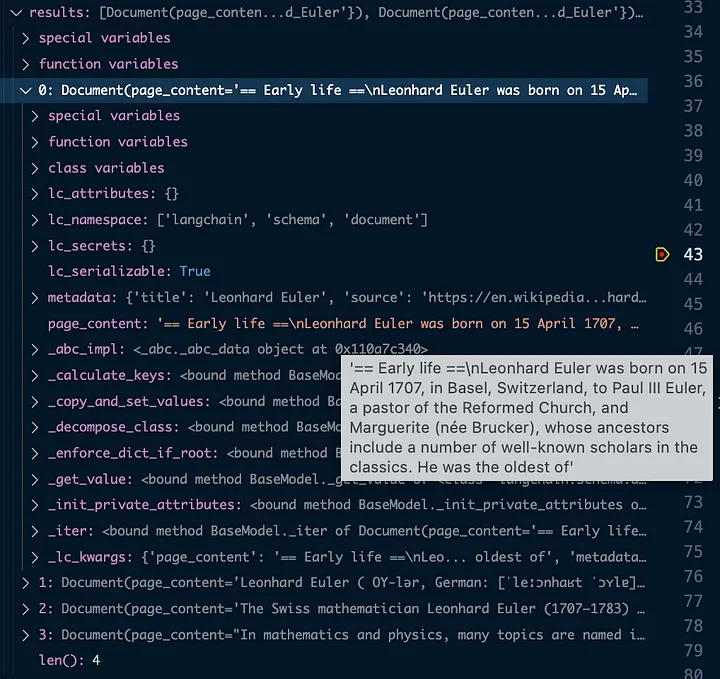
让我们看一下我们处理的文本块——存储在我们选择的节点的文本属性中:
text: "Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that for any real number x:where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively. This complex exponential function is sometimes denoted cis x ("cosine plus i sine"). The formula is still valid if x is a complex number, and so some authors refer to the more general complex version as Euler's formula. Euler's formula is ubiquitous in mathematics, physics, chemistry, and engineering. The physicist Richard Feynman called the equation "our jewel" and "the most remarkable formula in mathematics".When x = π, Euler's formula may be rewritten as eiπ + 1 = 0 or eiπ = -1, which is known as Euler's identity.== History ==In 1714, the English mathematician Roger Cotes presented a geometrical argument that can be interpreted (after correcting a misplaced factor of−1{\displaystyle {\sqrt {-1}}}) as:Exponentiating this equation yields Euler's formula. Note that the logarithmic statement is not universally correct for complex numbers, since a complex logarithm can have infinitely many values, differing by multiples of 2πi.Around 1740 Leonhard Euler turned his attention to the exponential function and derived the equation named after him by comparing the series expansions of the exponential and trigonometric expressions. The formula was first published in 1748 in his foundational work Introductio in analysin infinitorum.Johann Bernoulli had found thatAnd sincethe above equation tells us something about complex logarithms by relating natural logarithms to imaginary (complex) numbers. Bernoulli, however, did not evaluate the integral.Bernoulli's correspondence with Euler (who also knew the above equation) shows that Bernoulli did not fully understand complex logarithms. Euler also suggested that complex logarithms can have infinitely many values.The view of complex numbers as points in the complex plane was described about 50 years later by Caspar Wessel.== Definitions of complex exponentiation ==The exponential function ex for real values of x may be defined in a few different equivalent ways (see Characterizations of the exponential function). Several of these methods may be directly extended to give definitions of ez for complex values of z simply by substituting z in place of x and using the complex algebraic operations. In particular we may use any of the three following definitions, which are equivalent. From a more advanced perspective, each of these definitions may be interpreted as giving the unique analytic continuation of ex to the complex plane.=== Differential equation definition ===The exponential functionf(z)=ez{\displaystyle f(z)=e^{z}}is the unique differentiable function of a complex variable for which the derivative equals the function and=== Power series definition ===For complex zUsing the ratio test, it is possible to show that this power series has an infinite radius of convergence and so defines ez for all complex z.=== Limit definition ===For complex zHere, n is restricted to positive integers, so there is no question about what the power with exponent n means.== Proofs ==Various proofs of the formula are possible."复制
其对应的embedding值为:
embedding: [0.031864188611507416, 0.020641086623072624, -0.013721482828259468, -0.017606403678655624, -0.01527806743979454, 0.0022841887548565865, -0.016573039814829826, -0.016978537663817406, 0.011393147520720959, -0.0271813552826643, 0.022197671234607697, 0.02434287965297699, -0.014872570522129536, 0.021766014397144318, -0.03238740935921669, -0.0003873065288644284, 0.017972657456994057, -0.0038129764143377542, 0.011674378998577595, 0.022433120757341385, -0.005987615790218115, 0.002248217351734638, 0.0018639764748513699, -0.009025570936501026, -0.028463248163461685, 0.00985618494451046, 0.025834061205387115, -0.03204731643199921, 0.007776379119604826, -0.032701343297958374, 0.01769796572625637, 0.0055036358535289764, -0.03960786759853363, 0.00996736902743578, -0.013786885887384415, 0.025507047772407532, -0.0005432510515674949, 0.001888502505607903, 0.016612282022833824, 0.034715745598077774, 0.042511746287345886, 0.0047776661813259125, -0.016599200665950775, -0.007331640925258398, -0.008469647727906704, 0.006330979987978935, 0.0026602542493492365, -0.04954907298088074, 0.008672395721077919, 0.013786885887384415, 0.027809221297502518, 0.010189738124608994, -0.017998818308115005, -0.017004698514938354, -0.008521969430148602, -0.028829503804445267, 0.007383963093161583, -0.011510872282087803, 0.0073708826676011086, 0.0033224564976990223, 0.0010129241272807121, -0.00021419378754217178, -0.01768488623201847, -0.007109271828085184, -0.004846339114010334, 0.004300226457417011, -0.002230231650173664, 0.005065437871962786, -0.01954232156276703, 0.013329067267477512, 0.04486624151468277, 0.016429154202342033, 0.003930701408535242, 0.004473543725907803, 0.03202115371823311, -0.013708402402698994, -0.02414667047560215, 0.005248565226793289, 0.004512785468250513, 0.013329067267477512, 0.005945104174315929, -0.013198262080550194, -0.03453261777758598, -0.0023070797324180603, 0.006628562230616808, -0.029038792476058006, -0.017384033650159836, 0.03314607962965965, -0.03340769186615944, -0.013577597215771675, 0.024408282712101936, -0.006474865600466728, -0.007612872403115034, 0.004967333748936653, 0.002352861687541008, -0.01912374421954155, -0.0029643767047673464, 0.0013595583150163293, -0.002410088898614049, -0.02393738180398941, 0.012786224484443665, 0.000947521417401731, 0.0026537140365689993, -0.014663281850516796, -0.022995583713054657, -0.0110726747661829, 0.016455315053462982, 0.0035415554884821177, 0.011595896445214748, -0.0021321275271475315, -0.0034761526621878147, 0.03882303461432457, 0.013021674938499928, -0.02856789343059063, 0.02799234911799431, -0.024395201355218887, 0.03233508765697479, -0.008731258101761341, 0.006402922794222832, -0.016651524230837822, 0.00763903371989727, -0.004751504864543676, 0.026043349876999855, -0.0015132545959204435, 0.007684815675020218, -0.0006070186500437558, -0.013093617744743824, -0.011124996468424797, -0.010706419125199318, -0.02028791233897209, 0.022825537249445915, -0.01470252312719822, 0.007397043518722057, 0.01419238280504942, -0.0016653158236294985, 0.004146530292928219, -0.01459787879139185, -0.006308089010417461, -0.01993473805487156, -0.027102872729301453, 0.03319840133190155, 0.004911741707473993, -0.021399758756160736, 0.01408773846924305, -0.0018705168040469289, 0.022838616743683815, 0.010385946370661259, 0.02455216832458973, 0.004117099102586508, 0.001006383798085153, 0.027076711878180504, 0.018260428681969643, 0.0135645167902112, -0.006958845537155867, -0.0007059402414597571, 0.016167543828487396, 0.0010987650603055954, 0.04122985154390335, -0.006736476439982653, -0.012936650775372982, 0.0008420595549978316, 0.006092260126024485, -0.02535008080303669, -0.001144547015428543, 0.00688690273091197, 0.03241357207298279, 0.015042617917060852, 0.022655490785837173, -0.015814369544386864, 0.00046599411871284246, -0.019764691591262817, 0.028253959491848946, -0.025258516892790794, 0.017174744978547096, 0.013028214685618877, -0.008816282264888287, 0.0017642374150454998, 0.004247904289513826, -0.007985668256878853, 0.010353244841098785, 0.027521450072526932, 0.016586121171712875, 0.009326422587037086, 0.009830023162066936, -0.0004148982698097825, 0.005294347181916237, 0.030843906104564667, -0.00026549401809461415, -0.0028401114977896214, -0.024408282712101936, -0.014741765335202217, 0.01930687204003334, 0.009411446750164032, -0.0013407550286501646, -0.6140527129173279, -0.026592731475830078, -0.029431208968162537, -0.002045468892902136, -0.0019228389719501138, -0.018757490441203117, 0.0014862760435789824, 0.006514107342809439, -0.028829503804445267, -0.003162219887599349, -0.01874440908432007, -0.01648147590458393, 0.003242338076233864, -0.010987650603055954, 0.00782870128750801, -0.018796730786561966, -0.012419969774782658, -0.020274832844734192, 0.0011919639073312283, -0.0025016528088599443, -0.012596556916832924, -0.004705723375082016, -0.01751483976840973, 0.025611691176891327, 0.0004713080998044461, 0.032884471118450165, 0.01671692542731762, -0.015461194328963757, 0.011412768624722958, 0.003260323777794838, -0.003535015042871237, 0.02149132266640663, 0.00845656730234623, 0.012727362103760242, 0.026043349876999855, -0.035526737570762634, -0.001187876216135919, 0.014218543656170368, 0.027024390175938606, 0.03863990679383278, -0.012550774961709976, -0.025271598249673843, 0.031497932970523834, -0.011700540781021118, -0.021229712292551994, 0.003688711440190673, 0.03293679282069206, -0.00759979197755456, -0.006517377682030201, -0.028463248163461685, -0.00011762264330172911, -0.008705097250640392, 0.0007030788692645729, -0.0047286138869822025, 0.01952924206852913, -0.019215308129787445, -0.008371544070541859, -0.017802610993385315, -0.013302906416356564, -0.011857506819069386, -0.0028842585161328316, -0.0032243523746728897, -0.05012461915612221, 0.02571633644402027, -0.01649455726146698, 0.009712298400700092, -0.04865959659218788, 0.00040794923552311957, 0.011635137721896172, 0.007776379119604826, 0.012635799124836922, 0.0251669529825449, 0.004244634415954351, -0.01731863059103489, 0.014506315812468529, 0.016834650188684464, 0.032125797122716904, -0.0044179512187838554, 0.012635799124836922, -0.007207375951111317, 0.02231539599597454, -0.011321204714477062, -0.029038792476058006, -0.006245956290513277, 0.01829967088997364, -0.01831275224685669, -0.009705758653581142, 0.0075343893840909, 0.009398365393280983, 0.016612282022833824, 0.015369631350040436, 0.011569734662771225, 0.018626684322953224, -0.033067598938941956, 0.011484711430966854, 0.007325100712478161, -0.00004792790423380211, 0.006471595726907253, 0.0059254830703139305, -0.011229640804231167, -0.013656080700457096, -0.024225154891610146, 0.019385356456041336, 0.008947087451815605, -0.021177388727664948, 0.02211918868124485, -0.00803798995912075, 0.0029006090480834246, 0.0624203234910965, -0.0602751150727272, -0.02413359098136425, -0.027416804805397987, -0.025467805564403534, 0.005506906192749739, -0.008548131212592125, -0.031681060791015625, 0.020876536145806313, 0.004326387774199247, -0.0023348757531493902, -0.04104672372341156, 0.021399758756160736, -0.005425152834504843, -0.009280640631914139, -0.03584067150950432, 0.01650763675570488, 0.023008665069937706, 0.0030036182142794132, -0.012151818722486496, -0.03945089876651764, 0.008384624496102333, 0.024225154891610146, -0.008620074018836021, 0.005696573760360479, -0.011020352132618427, 0.002773073734715581, 0.0062590367160737514, 0.011844426393508911, -0.017344791442155838, 0.008168795146048069, -0.020392557606101036, -0.028829503804445267, -0.0069784666411578655, 0.004326387774199247, -0.013813046738505363, -0.029457369819283485, -0.03950322046875954, -0.010477510280907154, 0.012485372833907604, 0.004780936054885387, 0.007717516738921404, 0.003208001609891653, 0.013656080700457096, -0.01975161023437977, 0.03675631061196327, 0.021975301206111908, 0.011327745392918587, 0.006762637756764889, -0.008391164243221283, -0.020366396754980087, -0.0059745353646576405, -0.004754775203764439, 0.03353849798440933, -0.0069196042604744434, 0.008221117779612541, -0.024617571383714676, -0.00654353853315115, -0.025075389072299004, 0.004898661281913519, -0.0018901375588029623, -0.051825087517499924, 0.0068411207757890224, 0.008665855973958969, 0.004283875692635775, 0.016416074708104134, 0.01569664478302002, 0.024996906518936157, -0.02111198753118515, -0.008914385922253132, -0.005706384312361479, -0.010562533512711525, 0.026893584057688713, -0.006703775376081467, -0.042145490646362305, 0.008116473443806171, 0.01792033575475216, 0.010536372661590576, 0.004993495065718889, -0.000909097318071872, -0.018038060516119003, 0.007717516738921404, 0.007325100712478161, 0.027312161400914192, 0.007253157906234264, -0.007436285261064768, -0.0005771786672994494, 0.011301583610475063, 0.03199499472975731, -0.0020307532977312803, 0.012805845588445663, 0.05075248330831528, 0.018378155305981636, 0.006985006853938103, 0.02070648968219757, -0.024434443563222885, 0.019359195604920387, -0.0036396593786776066, -0.003242338076233864, -0.0041628810577094555, 0.06597822904586792, 0.0019162986427545547, 0.010889546945691109, -0.015840530395507812, -0.0381690077483654, -0.01853512041270733, 0.010431728325784206, 0.03544825688004494, 0.029064953327178955, 0.015238825231790543, 0.01691313460469246, -0.002534354105591774, 0.005107949487864971, -0.006402922794222832, 0.0005469299503602087, -0.00026283704210072756, -0.006971926428377628, 0.02030099369585514, 0.01627218723297119, 0.007501687854528427, -0.0008412420284003019, -0.04057582467794418, -0.001448669470846653, 0.007442825473845005, -0.009012489579617977, 0.031471770256757736, 0.006501026917248964, 0.052217502146959305, 0.0044179512187838554, -0.0019490000559017062, 0.0382474884390831, -0.014113899320363998, -0.02290401980280876, 0.0220930278301239, -0.00763903371989727, -0.004028805531561375, -0.005882971454411745, -0.013100157491862774, 0.012727362103760242, 0.00042429991299286485, 0.021648287773132324, 0.012753523886203766, -0.013067456893622875, 0.005477475002408028, -0.011909828521311283, -0.00288752862252295, 0.01669076457619667, 0.01387844979763031, 0.0035742567852139473, 0.018456637859344482, 0.02011786587536335, 0.03516048192977905, 0.022851698100566864, -0.023898141458630562, 0.006510837469249964, -0.0017642374150454998, -0.007004627492278814, 0.0005914855282753706, -0.0004966516280546784, -0.01848279871046543, -0.024473683908581734, -0.03986947610974312, -0.009686137549579144, -0.021844496950507164, 0.0018852323992177844, -0.002957836491987109, 0.020379476249217987, -0.009104053489863873, 0.023649610579013824, 0.008848982863128185, 0.0060301274061203, 0.001947364886291325, -0.03924161195755005, -0.020680328831076622, -0.0014225083868950605, 0.024042027071118355, -0.007272778544574976, -0.019856255501508713, 0.002895703772082925, 0.010314003564417362, 0.001518977340310812, 0.01359067764133215, 0.0001279440039070323, 0.0057815974578261375, -0.018077302724123, -0.012917030602693558, -0.02129511348903179, -0.01176594290882349, 0.009077892638742924, 0.0020013221073895693, -0.00795296672731638, -0.0044441125355660915, 0.018849054351449013, -0.01752791926264763, -0.017161663621664047, 0.002944755833595991, 0.037305690348148346, -0.012197600677609444, -0.0013333972310647368, -0.00843694619834423, 0.004875770304352045, -0.013865369372069836, -0.0042707952670753, -0.029509691521525383, -0.01467636227607727, -0.016219865530729294, 0.0342710055410862, -0.006736476439982653, 0.027861542999744415, -0.013629919849336147, 0.02236771769821644, -0.02011786587536335, -0.015421953052282333, -0.0030657509341835976, 0.0022449472453445196, 0.010516751557588577, 0.04952291399240494, 0.017227066680788994, -0.016049819067120552, 0.026919744908809662, 0.014820248819887638, -0.010791443288326263, -0.016350671648979187, -0.026697376742959023, 0.021164309233427048, 0.03060845658183098, 0.0015786573057994246, -0.009659976698458195, 0.006693964824080467, -0.0025016528088599443, -0.01874440908432007, -0.004931362345814705, 0.01086992584168911, -0.011275422759354115, 0.03361697867512703, 0.0100654736161232, -0.008476188406348228, 0.014689442701637745, 0.037122562527656555, 0.017057020217180252, -0.0031278834212571383, 0.0006863194284960628, 0.0231133084744215, 0.028881825506687164, -0.010555993765592575, -0.01828659139573574, -0.01287124864757061, 0.011491252109408379, -0.00045168728684075177, -0.01054945308715105, -0.022851698100566864, 0.02351880632340908, 0.007802540436387062, 0.007213916163891554, 0.006608941126614809, -0.03434948995709419, -0.014205463230609894, 0.008123013190925121, 0.0018214647425338626, -0.00462397001683712, -0.009954288601875305, -0.030922388657927513, -0.011844426393508911, -0.006311358883976936, -0.014336268417537212, 0.00893400702625513, -0.00007557075878139585, -0.02133435569703579, -0.008319221436977386, -0.01871824823319912, -0.009679597802460194, 0.018966779112815857, 0.014951054006814957, -0.02270781248807907, -0.007436285261064768, -0.009849644266068935, -0.0201440267264843, -0.014833329245448112, 0.02173985168337822, -0.005510176066309214, 0.024081269279122353, -0.02958817407488823, -0.011530493386089802, 0.000004841331701754825, -0.0190975833684206, -0.01608906127512455, 0.019071422517299652, -0.026291878893971443, -0.03633773326873779, 0.006631832104176283, 0.03879687190055847, 0.015997497364878654, 0.005320508498698473, -0.0061151511035859585, -0.0031000871676951647, -0.0030036182142794132, -0.010778362862765789, -0.03157641738653183, -0.019385356456041336, -0.03895384073257446, -0.003930701408535242, 0.021268952637910843, 0.016573039814829826, -0.007861402817070484, 0.011419308371841908, 0.015251905657351017, 0.0014756480231881142, 0.006046478170901537, 0.007769838906824589, -0.0044146813452243805, -0.019764691591262817, 0.017763368785381317, -0.0021909899078309536, 0.01517342310398817, 0.023623449727892876, -0.019398435950279236, -0.006932684686034918, -0.0321781225502491, 0.008848982863128185, 0.008502349257469177, 0.00224004196934402, 0.0051406510174274445, 0.023087147623300552, 0.0016497827600687742, -0.01076528150588274, -0.030477650463581085, -0.009516091085970402, -0.021373597905039787, 0.04081127420067787, 0.017841853201389313, -0.0011658028233796358, 0.005873160902410746, 0.01751483976840973, 0.008208037354052067, -0.0043034967966377735, -0.0241074301302433, -0.012694661505520344, 0.0022939990740269423, 0.002241677138954401, -0.020588764920830727, -0.015212664380669594, 0.008371544070541859, -0.014440912753343582, -0.020654167979955673, -0.013852288946509361, 0.011013812385499477, 0.04544178396463394, 0.018064221367239952, 0.008404244668781757, -0.01416622195392847, -0.03283214941620827, -0.006151122506707907, -0.030451489612460136, -0.003933971282094717, -0.0015165247023105621, 0.003960132598876953, 0.02193606086075306, 0.01947692036628723, -0.010163577273488045, -0.005932023283094168, 0.004313306882977486, -0.029640497639775276, -0.016612282022833824, 0.019660046324133873, 0.012851627543568611, -0.011798644438385963, 0.0044768135994672775, -0.009372204542160034, 0.011667839251458645, -0.014741765335202217, 0.0034172902815043926, -0.016978537663817406, -0.004548756871372461, -0.0029431208968162537, 0.014048496261239052, -0.0005399809451773763, 0.01973853074014187, 0.022289235144853592, 0.0062263356521725655, 0.04340122267603874, -0.019267631694674492, 0.02372809313237667, -0.029640497639775276, 0.02074573189020157, -0.02638344280421734, 0.014257784932851791, 0.04060198739171028, 0.021582886576652527, 0.02294326201081276, -0.008443486876785755, 0.01519958395510912, 0.018064221367239952, -0.01690005324780941, 0.005307428073137999, -0.004408141132444143, -0.0502554215490818, -0.0001834340946516022, 0.023649610579013824, 0.002058549551293254, 0.008397704921662807, 0.0003603279183153063, -0.001079144305549562, -0.017344791442155838, -0.005742355715483427, 0.008822822012007236, 0.01688697375357151, 0.014741765335202217, -0.013551436364650726, 0.03594531491398811, 0.010529831983149052, 0.023885060101747513, -0.007076570298522711, 0.0014429467264562845, -0.010399026796221733, -0.019450757652521133, 0.021412838250398636, -0.020798053592443466, 0.03484655171632767, -0.002493477426469326, 0.011589355766773224, -0.013943852856755257, -0.028070831671357155, 0.00759979197755456, -0.017854932695627213, 0.00342383049428463, -0.027286000549793243, 0.0023038096260279417, -0.02274705469608307, 0.001616263878531754, -0.004869230091571808, -0.02414667047560215, 0.00021930337243247777, 0.01377380546182394, 0.008907845243811607, -0.025245435535907745, -0.013747644610702991, 0.02575557678937912, -0.014467073604464531, 0.042511746287345886, -0.00906481221318245, 0.029038792476058006, 0.033512335270643234, 0.0008960167760960758, -0.008031449280679226, -0.008417325094342232, 0.006697234697639942, 0.01226300373673439, 0.012014472857117653, -0.0018688817508518696, -0.025847140699625015, -0.01136698666960001, 0.017043938860297203, 0.005274726543575525, -0.02697206661105156, -0.002078170422464609, 0.03725336864590645, 0.0015590365510433912, 0.014650201424956322, -0.00015277658530976623, 0.016455315053462982, -0.01197523158043623, 0.007756758481264114, -0.02255084551870823, -0.004218473099172115, -0.032675180584192276, -0.002271108329296112, -0.009404906071722507, 0.03699176013469696, -0.008875144645571709, 0.033904753625392914, -0.019398435950279236, 0.013152480125427246, -0.010320543311536312, -0.02313946932554245, -0.024696053937077522, -0.0058633508160710335, -0.020196348428726196, 0.02030099369585514, -0.02574249729514122, 0.012426510453224182, 0.021857576444745064, 0.01046442985534668, -0.024813778698444366, -0.012341486290097237, 0.008482728153467178, 0.03060845658183098, -0.024996906518936157, 0.005618090741336346, 0.0062263356521725655, -0.010634476318955421, -0.022838616743683815, -0.00863969512283802, -0.022053785622119904, -0.025062309578061104, -0.0010202819248661399, 0.00003852626832667738, 0.026069510728120804, 0.01950308121740818, -0.008881684392690659, -0.0008559576235711575, -0.005516716279089451, 0.002298904350027442, -0.008319221436977386, -0.012943191453814507, -0.01692621409893036, -0.02937888540327549, -0.008848982863128185, -0.013865369372069836, 0.020183268934488297, 0.020837295800447464, -0.007253157906234264, -0.010555993765592575, -0.009934667497873306, 0.029248081147670746, -0.00713543314486742, 0.024853020906448364, 0.02452600747346878, 0.0057554361410439014, 0.0025163684040308, 0.0018361803377047181, -0.008070691488683224, -0.007050409447401762, 0.040732793509960175, -0.015539677813649178, -0.023898141458630562, -0.016625363379716873, -0.0069196042604744434, 0.00853505078703165, 0.0014625675976276398, -0.007907184772193432, -0.016769248992204666, 0.0022433120757341385, -0.0017642374150454998, -0.020392557606101036, -0.00668742461130023, -0.006762637756764889, 0.0042740656062960625, -0.005284537095576525, 0.013943852856755257, -0.012256463058292866, 0.027469128370285034, 0.015552758239209652, -0.01247883215546608, -0.01086992584168911, -0.003770464798435569, 0.004208662547171116, -0.018221188336610794, 0.009404906071722507, -0.0014306837692856789, -0.015147262252867222, -0.01973853074014187, -0.015186503529548645, -0.017541000619530678, 0.02859405428171158, 0.02235463820397854, 0.01848279871046543, -0.01297589298337698, 0.015801288187503815, 0.009110594168305397, 0.028096992522478104, 0.007272778544574976, -0.03311992064118385, 0.007436285261064768, 0.008600452914834023, -0.022236913442611694, -0.006419273559004068, 0.010588694363832474, 0.007266238331794739, 0.026304960250854492, -0.00943760760128498, -0.0019113934831693769, -0.0029725520871579647, -0.03890151530504227, 0.0020977910608053207, -0.04120369255542755, 0.02194914035499096, 0.01971236988902092, 0.009607654064893723, -0.008286519907414913, 0.008724718354642391, -0.02052336186170578, 0.019633885473012924, -0.02476145699620247, 0.002146843122318387, 0.013839208520948887, 0.0036527400370687246, -0.01993473805487156, -0.009823483414947987, -0.020000141113996506, -0.011779023334383965, 0.032492052763700485, -0.00005773830707767047, 0.0070896511897444725, 0.021399758756160736, -0.026998227462172508, -0.005624630954116583, -0.015081859193742275, 0.014310107566416264, 0.0019898766186088324, 0.027259839698672295, 0.024434443563222885, -0.04567723348736763, 0.004839798901230097, -0.02031407319009304, 0.00007424226350849494, -0.0301375575363636, 0.008763959631323814, 0.004048426169902086, -0.024617571383714676, -0.009090973064303398, 0.0034990436397492886, -0.005036006681621075, 0.013322526589035988, -0.02736448310315609, 0.03675631061196327, -0.02393738180398941, 0.03366930037736893, 0.030032912269234657, 0.010850305669009686, 0.004885580390691757, -0.014126979745924473, 0.012099497020244598, -0.029509691521525383, -0.01176594290882349, 0.025271598249673843, 0.0007754305843263865, 0.0037050622049719095, -0.031497932970523834, 0.007756758481264114, -0.010490590706467628, -0.010778362862765789, -0.03199499472975731, -0.008593913167715073, -0.01570972427725792, 0.03482038900256157, 0.0090713519603014, -0.037514980882406235, -0.007527849171310663, -0.005124300252646208, -0.005428422708064318, -0.014493235386908054, -0.011406227946281433, 0.020366396754980087, 0.008757419884204865, 0.0032635938841849566, -0.010196278803050518, -0.015421953052282333, -0.031053194776177406, 0.013760725036263466, -0.008397704921662807, -0.008214577101171017, 0.013433711603283882, 0.20813749730587006, 0.011281963437795639, 0.01377380546182394, 0.006873822305351496, -0.004872499965131283, 0.009836563840508461, -0.019254550337791443, -0.0030248742550611496, -0.02088961750268936, 0.0071223522536456585, -0.01752791926264763, -0.001199321704916656, -0.03578834980726242, 0.012217221781611443, -0.013230962678790092, -0.037358012050390244, -0.01827351003885269, -0.024839939549565315, -0.00349577353335917, -0.01035978551954031, 0.021242791786789894, -0.0036560101434588432, -0.004362359177321196, -0.007501687854528427, 0.018417395651340485, -0.003848948050290346, -0.013512195087969303, -0.016991617158055305, 0.0201309472322464, -0.004395060241222382, -0.009450688026845455, -0.016965456306934357, -0.02733832225203514, 0.034689582884311676, -0.03665166348218918, -0.0021010611671954393, 0.028698697686195374, -0.00943760760128498, 0.03311992064118385, 0.009267560206353664, 0.006170743145048618, -0.03202115371823311, 0.0016734912060201168, -0.020222509279847145, 0.03157641738653183, 0.018679006025195122, 0.006321169435977936, -0.018391234800219536, -0.011648218147456646, 0.022053785622119904, -0.03924161195755005, -0.008221117779612541, -0.0160759799182415, 0.03317224234342575, 0.021661369130015373, -0.0011911464389413595, 0.02694590575993061, 0.024669893085956573, 0.014310107566416264, 0.03654702007770538, -0.023885060101747513, 0.009705758653581142, 0.0021370328031480312, -0.005637711379677057, -0.0021844496950507164, 0.013904610648751259, -0.027495289221405983, 0.008378083817660809, -0.011648218147456646, -0.003848948050290346, -0.005742355715483427, -0.03704408183693886, -0.023466482758522034, 0.01773720793426037, -0.019149906933307648, -0.014205463230609894, 0.02576865814626217, -0.00471880380064249, 0.012289164587855339, 0.015971336513757706, -0.0008097669924609363, -0.005605010315775871, -0.016167543828487396, 0.0016841191099956632, -0.018822893500328064, -0.0201440267264843, 0.00709619140252471, 0.017357872799038887, -0.005732545163482428, 0.0004974691546522081, 0.008489268831908703, -0.004408141132444143, -0.008757419884204865, -0.0052812667563557625, 0.011667839251458645, 0.005961454939097166, 0.012348026968538761, -0.007737137842923403, -0.024264395236968994, 0.033904753625392914, -0.004712263587862253, 0.042302455753088, 0.030660778284072876, -0.008319221436977386, 0.006131501868367195, -0.016625363379716873, 0.01015703659504652, 0.01567048393189907, 0.012590017169713974, -0.027207516133785248, -0.026618892326951027, 0.010928788222372532, -0.005068708211183548, -0.024081269279122353, -0.0261741541326046, -0.010516751557588577, 0.006579509936273098, 0.018862133845686913, 0.009986990131437778, 0.006736476439982653, -0.007508228067308664, -0.023060986772179604, -0.030686939135193825, 0.010307462885975838, -0.0010137415956705809, -0.016586121171712875, -0.06472249329090118, 0.011432389728724957, -0.008829362690448761, -0.010745661333203316, 0.023649610579013824, -0.008077231235802174, 0.015356549993157387, -0.0068411207757890224, 0.005376100540161133, -0.014231624081730843, -0.024447523057460785, 0.0006209167186170816, -0.007926804944872856, 0.023047905415296555, -0.02434287965297699, -0.005869891028851271, 0.007874483242630959, -0.0034696124494075775, 0.00291532464325428, -0.004457192961126566, -0.001396347302943468, 0.016546878963708878, 0.0024656811729073524, -0.03346001356840134, -0.01348603330552578, -0.015801288187503815, -0.0010031136916950345, -0.04609581083059311, 0.00018813491624314338, -0.031105516478419304, -0.030817745253443718, -0.047351542860269547, 0.04559875279664993, -0.00643889419734478, -0.030216040089726448, 0.006196904461830854, 0.012681580148637295, -0.023492643609642982, -0.01948999986052513, -0.01005239225924015, -0.16251258552074432, 0.00044759962474927306, 0.012943191453814507, -0.009202158078551292, -0.007678274996578693, 0.013459872454404831, 0.035866834223270416, 0.0033943993039429188, 0.007573631126433611, -0.004924822133034468, 0.021622126922011375, 0.00029104194254614413, -0.023087147623300552, -0.02614799328148365, -0.006834580563008785, 0.0035415554884821177, 0.0029431208968162537, 0.01975161023437977, 0.04463079199194908, 0.02251160331070423, 0.038142845034599304, -0.03356465697288513, 0.0231656301766634, 0.002552339807152748, -0.003384588984772563, -0.000005460868578666123, -0.012805845588445663, 0.0007014438160695136, 0.02255084551870823, -0.012112577445805073, -0.0003035093250218779, -0.02449984662234783, 0.026278799399733543, -0.014388591051101685, -0.0080641508102417, -0.004198852460831404, -0.002763263415545225, -0.018077302724123, -0.01587977260351181, 0.011968690901994705, 0.03039916791021824, 0.031471770256757736, -0.008273439481854439, 0.0051995133981108665, 0.0026553489733487368, 0.006814959924668074, 0.015971336513757706, 0.001718455576337874, 0.002045468892902136, -0.017763368785381317, 0.03366930037736893, -0.03155025467276573, 0.016023658215999603, 0.012439590878784657, 0.02733832225203514, -0.009130214340984821, 0.020052462816238403, 0.018038060516119003, -0.015997497364878654, -0.012177979573607445, -0.00482344813644886, -0.03194267302751541, 0.005006575491279364, -0.0030297792982310057, 0.035500578582286835, 0.002609567018225789, -0.01297589298337698, 0.029248081147670746, -0.03181186690926552, 0.015932094305753708, 0.012897409498691559, -0.014467073604464531, 0.0161152221262455, -0.028070831671357155, 0.01408773846924305, 0.030817745253443718, -0.009417986497282982, -0.010143956169486046, 0.013956933282315731, -0.018338913097977638, -0.033695463091135025, 0.005124300252646208, 0.019267631694674492, -0.009509550407528877, -0.014113899320363998, -0.015343469567596912, -0.004993495065718889, 0.004489894490689039, -0.011458550579845905, -0.004964063875377178, 0.011720160953700542, -0.028463248163461685, -0.006641642656177282, 0.006520647555589676, -0.020955020561814308, 0.01852204091846943, 0.0031883809715509415, 0.002763263415545225, 0.004725344013422728, -0.00533685926347971, 0.014244704507291317, -0.008391164243221283, -0.014610960148274899, 0.010641016997396946, 0.03884919360280037, 0.005225674714893103, -0.021582886576652527, 0.02052336186170578, 0.04889504611492157, -0.005765246693044901, -0.009123674593865871, -0.004149800166487694, 0.02434287965297699, 0.025585530325770378, -0.01747559756040573, 0.010935328900814056, -0.014977214857935905, 0.004506244789808989, 0.024277476593852043, 0.0014241434400901198, 0.06268193572759628, 0.013361768797039986, -0.01416622195392847, 0.00785486213862896, 0.008966708555817604, -0.0281754769384861, -0.10412107408046722, -0.010274761356413364, 0.000498695473652333, 0.027913866564631462, 0.02391122095286846, 0.01646839641034603, -0.028489409014582634, -0.015932094305753708, -0.016036737710237503, 0.033276885747909546, -0.02431671880185604, -0.01337484922260046, -0.004689372610300779, 0.00021112804824952036, -0.0022547575645148754, 0.006157662719488144, -0.003371508326381445, -0.004663211293518543, -0.05156347528100014, 0.02235463820397854, 0.00893400702625513, 0.0017920335521921515, 0.015997497364878654, 0.014100818894803524, 0.005807758308947086, -0.0015197949251160026, -0.030660778284072876, 0.01671692542731762, 0.013577597215771675, 0.0007026700768619776, -0.014283946715295315, -0.007240077015012503, -0.009908506646752357, -0.04298264533281326, 0.013799966312944889, -0.016429154202342033, 0.01145200990140438, 0.016402993351221085, 0.011432389728724957, -0.022812455892562866, 0.01565740257501602, 0.0017527919262647629, 0.02173985168337822, 0.007168134208768606, -0.008685476146638393, -0.00311480276286602, -0.0007325100596062839, 0.04729922115802765, -0.015997497364878654, -0.009777701459825039, -0.031471770256757736, -0.013034755364060402, -0.037907395511865616, 0.015474275685846806, 0.017593322321772575, 0.0025850411038845778, -0.01772412844002247, 0.016965456306934357, -0.015408872626721859, -0.02136051654815674, -0.014244704507291317, -0.00648794649168849, -0.028489409014582634, -0.005212593823671341, 0.008947087451815605, 0.012701201252639294, -0.012295704334974289, 0.006245956290513277, 0.010281302034854889, -0.011085755191743374, -0.0068411207757890224, 0.0011281963670626283, -0.007998748682439327, 0.01827351003885269, -0.055199865251779556, 0.02074573189020157, -0.008005288429558277, -0.012106036767363548, 0.029091114178299904, -0.020837295800447464, -0.006510837469249964, -0.020562604069709778, 0.013734564185142517, 0.007083110976964235, 0.013499113731086254, 0.04444766417145729, 0.017541000619530678, -0.01015703659504652, 0.027521450072526932, -0.0271813552826643, -0.004594538826495409, -0.001396347302943468, 0.06718163937330246, -0.008986328728497028, -0.004571647848933935, -0.03155025467276573, 0.0115501144900918, -0.03364314138889313, 0.013145939446985722, 0.009195617400109768, -0.013708402402698994, -0.004905201494693756, -0.052008215337991714, 0.01971236988902092, -0.0018230997957289219, -0.01747559756040573, 0.00023749349929858, -0.008986328728497028, 0.03686095401644707, -0.026200314983725548, 0.006474865600466728, 0.010601774789392948, -0.003443451365455985, -0.0030232390854507685, -0.014362429268658161, -0.01247229240834713, -0.017370952293276787, -0.03722720965743065, 0.016808489337563515, 0.006111880764365196, 0.0037573841400444508, 0.005003305617719889, 0.0007754305843263865, 0.031236322596669197, 0.01669076457619667, 0.006814959924668074, -0.014964134432375431, -0.017200905829668045, 0.002591581316664815, 0.0016579580260440707, -0.02374117448925972, -0.005915672983974218, -0.008181875571608543, -0.015788208693265915, 0.014375509694218636, 0.051223382353782654, -0.021452080458402634, -0.02372809313237667, 0.022786295041441917, 0.034323327243328094, 0.01646839641034603, 0.032125797122716904, -0.0005796313052996993, -0.021007342264056206, 0.004950983449816704, 0.018757490441203117, 0.00043043142068199813, -0.018783651292324066, -0.003960132598876953, -0.0016342495800927281, 0.013708402402698994, 0.02773073874413967, 0.014807167463004589, -0.00584045983850956, -0.022668570280075073, 0.005124300252646208, 0.019372275099158287, 0.0032635938841849566, 0.016154462471604347, -0.010667177848517895, 0.026488088071346283, -0.012903950177133083, 0.036520857363939285, 0.003629849059507251, 0.011818265542387962, 0.0014151505893096328, -0.005071978084743023, -0.027626093477010727, -0.04954907298088074, 0.005860080476850271, 0.011033432558178902, -0.015565838664770126, -0.009496469981968403, 0.013970013707876205, -0.004754775203764439, 0.010000070556998253, 0.019803933799266815, -0.013616839423775673, -0.020392557606101036, -0.0021321275271475315, 0.0031278834212571383, 0.007410124409943819, 0.024212073534727097, -0.002486936980858445, -0.003255418734624982, 0.009516091085970402, 0.02234155684709549, 0.013250583782792091, -0.020170187577605247, -0.002581770997494459, -0.0011739782057702541, 0.021033503115177155, 0.007737137842923403, 0.02171369083225727, -0.018862133845686913, 0.007357802242040634, 0.019149906933307648, -0.005242025014013052, -0.02794002741575241, -0.009110594168305397, -0.004149800166487694, 0.0017724127974361181, 0.0014511221088469028, 0.011458550579845905, 0.0191368255764246, -0.029457369819283485, -0.009411446750164032, -0.00010254936933051795, -0.02031407319009304, -0.019633885473012924, 0.0007721604197286069, 0.01751483976840973, 0.009378745220601559, 0.013244044035673141, -0.0009916682029142976, -0.0019081233767792583, -0.007782919332385063, 0.029509691521525383, 0.0231133084744215, -0.01790725439786911, -0.004882310517132282, 0.029614334926009178, 0.008606993593275547, 0.009136755019426346, 0.0010284571908414364, -0.011883667670190334, 0.029875947162508965, 0.008947087451815605, 0.02572941593825817, -0.018587442114949226, 0.03275366500020027, -0.028437087312340736, -0.009823483414947987, 0.009110594168305397, 0.0019898766186088324, -0.008404244668781757, -0.013348688371479511, -0.005546147469431162, -0.006465055514127016, -0.01005239225924015, -0.0035742567852139473, 0.08512813597917557, 0.025507047772407532, -0.017410194501280785, 0.04484008252620697, 0.010130875743925571, 0.020628007128834724, 0.009431066922843456, -0.006893442943692207, 0.006579509936273098, -0.05394413322210312, -0.001287615392357111, 0.0020961561240255833, -0.004852879326790571, 0.0026880502700805664, -0.01075874175876379, 0.015539677813649178, -0.005588659550994635, 0.026448845863342285, -0.021268952637910843, -0.006906523369252682, 0.021556725725531578, 0.017240148037672043, 0.0062557668425142765, 0.00423155352473259, -0.02232847735285759, -0.015605080872774124, 0.02637036330997944, 0.012956271879374981, -0.001310506253503263, -0.01811654306948185, -0.015317308716475964, -0.009640355594456196, -0.021282033994793892, -0.03196883201599121, 0.005428422708064318, -0.02171369083225727, 0.018600523471832275, -0.01887521520256996, 0.007861402817070484, 0.010719500482082367, -0.0033518876880407333, 0.0017446166602894664, 0.0037344933953136206, -0.043950602412223816, -0.026605812832713127, 0.006298278458416462, -0.022890940308570862, -0.0005546965403482318, -0.05284537002444267]复制
现在我们有了向量嵌入数据。这对我们的搜索有何帮助?接下来会有解答。
02
针对 Neo4j 向量数据运行示例查询
向量检索利用机器学习 (ML)来捕获非结构化数据(包括文本和图像)的含义和上下文,并将其转换为数字表示。向量检索经常用于语义搜索,它使用近似最近邻 (ANN) 算法查找相似数据。与传统的关键字搜索相比,向量检索会产生更相关的结果并且执行速度更快。
接下来进行向量相似度搜索。
让我们查询 Neo4j 图,看看是否可以根据我们导入的数据回答“Euler 在哪里长大?”这个问题。
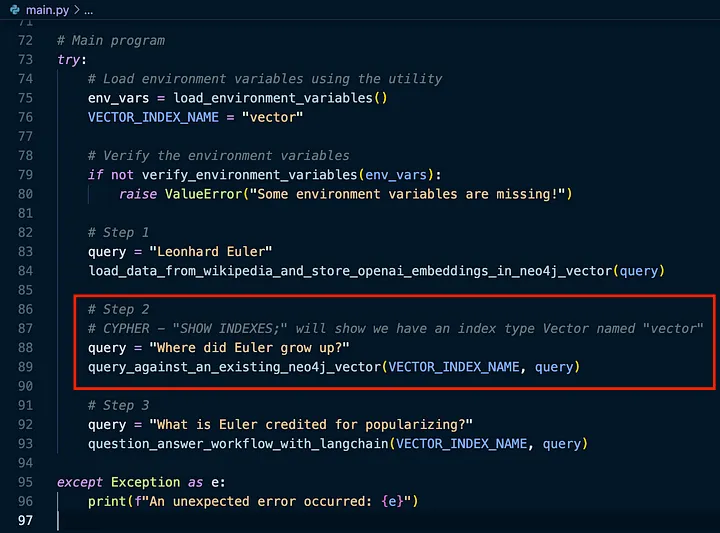
首先,让我们初始化 Neo4j Vector。Neo4j 向量索引的默认名称是:vector - Neo4j 凭证传递的内容。
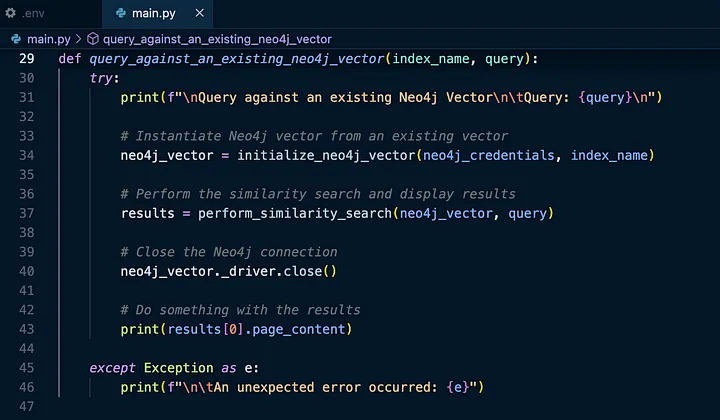
使用 Neo4jVector 向量存储,我们将需要使用 from_existing_index 方法:
一旦我们有了 Neo4j Vector Index,我们就可以使用 LangChain 模块的 similarity_search 方法执行相似性搜索:
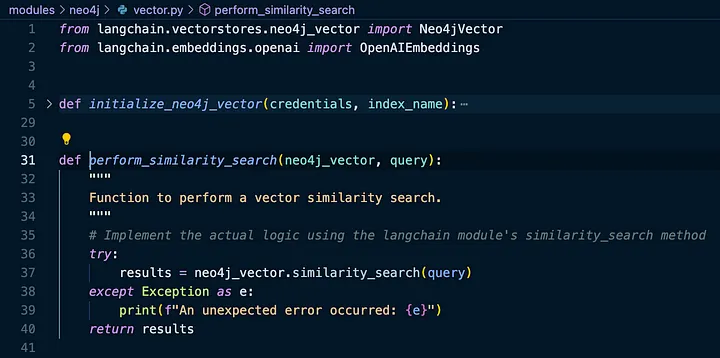
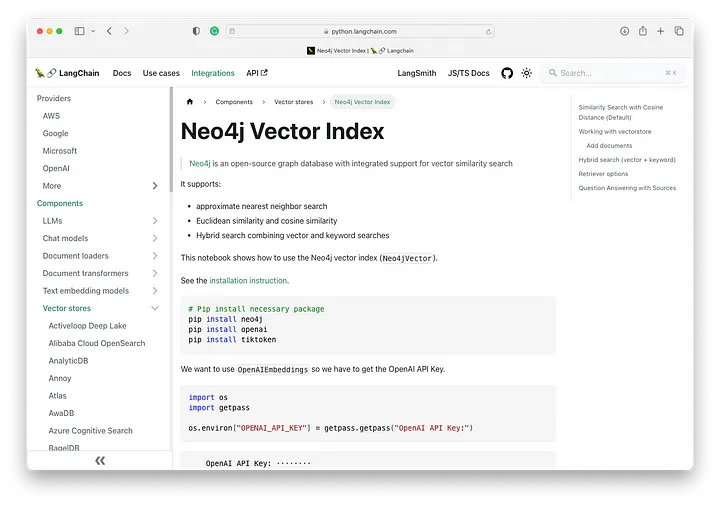
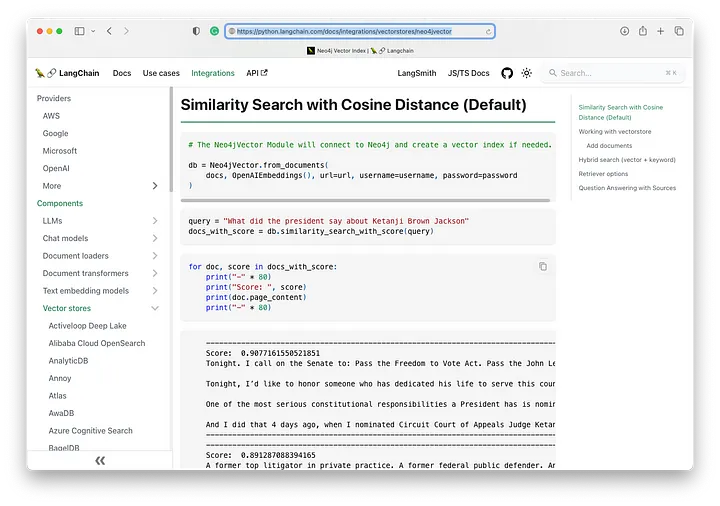
我们来看看我们的查询结果吧
我们的应用程序将显示第一个结果的已处理的数据块 page_content。
03
使用 LangChain 和 Neo4j 简单问答工作流程
在最后一步,我们将使用 LangChain 和 Neo4j 后端探索示例问题/答案工作流程。

这里涉及到一个初始化和执行 LangChain 问答工作流程的简单计划。
LangChain 问答概述包含我们将要做的事情的精美可视化:
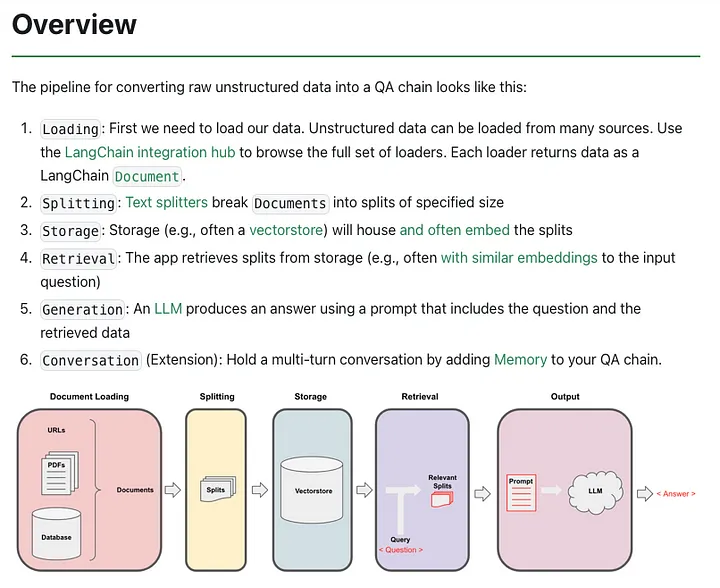
我们将从第 4 步开始,因为 neo4j_vector 是我们的向量存储。我们将初始化用于搜索的 Neo4j 向量索引,然后生成 LLM 的提示,包括我们的原始查询和检索到的数据。
首先,让我们初始化 Neo4j Vector。
使用 Neo4jVector 向量存储,我们将需要使用 from_existing_index 方法:

一旦我们有了 Neo4j Vector Index,我们就可以初始化我们的工作流程:
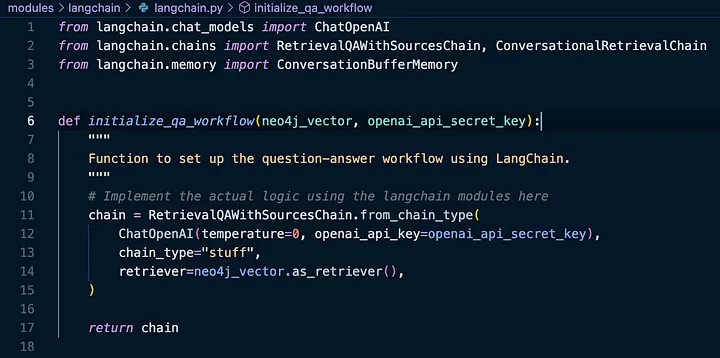
设置工作流程后,我们可以通过生成 LLM 提示来执行它,其中包括我们的原始查询和检索到的数据:
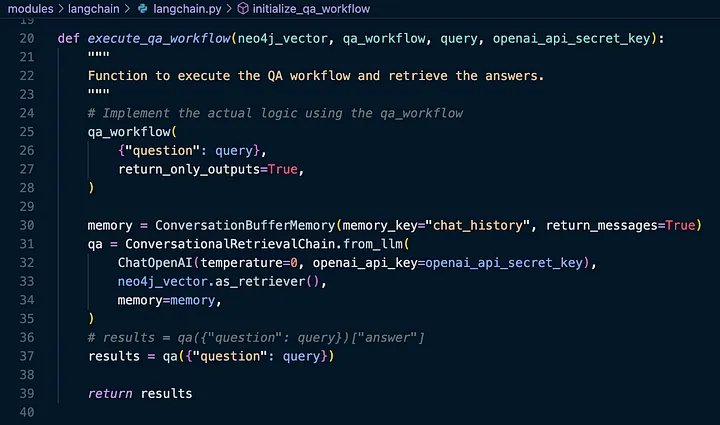
我们在问答工作流程中保留了一些对话记忆 - 并查看响应是什么:
Question/Answer workflow with LangChainwith LangChainQuery: What is Euler credited for popularizing?Euler is credited for popularizing several mathematical concepts and notations. Some of the things he is credited for popularizing include:1. The use of the Greek letter π (pi) to represent the ratio of a circle's circumference to its diameter.2. The notation f(x) to represent a function.3. The use of the letter e to represent the base of the natural logarithm, now known as Euler's number.4. The use of the letter i to represent the imaginary unit (√-1).5. The use of lowercase letters to represent the sides of a triangle and uppercase letters to represent the angles.6. The use of the Greek letter Σ (sigma) to represent summations.7. The use of the Greek letter Δ (delta) to represent finite differences.These are just a few examples of the many mathematical concepts and notations that Euler is credited for popularizing.复制
看,检索增强生成 (RAG) 和 Neo4j 向量的入门就这么简单。
向量检索实验室
微信号:VectorSearch
扫码关注 了解更多







