目录
1、均方误差
2、标准化均方误差
3、案例演示
作者:
编辑:
版本:
xiaoluo
xiaoluo
python3
均方误差
均方误差是指参数估计值与参数真值之差平方的期望值,记为MSE。MSE是衡量“平均误差”的一种较为方便的方法,MSE可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。
均方误差(MSE, mean squared error)的公式可以表示为:
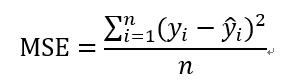
由于对误差值进行了平方,它避免了正负误差不能相加的问题,加强了误差值较大的点在指标中的作用,从而提高了这个指标的灵敏性。
标准化均方误差
标准化均方误差(NMSE, normalized mean squared error)的公式可以表示为:
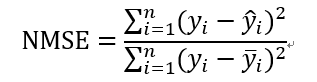
标准化均方误差对均方差进行了标准化改进,计算出了欲评估模型和以均值为基础的模型之间的准确性比率。标准化均方误差取值范围一般为0~1,比率越小,说明模型越优于以均值进行预测的策略。
NMSE的值大于1,意味着有模型还不如没有模型(简单地把所有观测值的均值作为预测值)。
案例演示
对于回归问题,常用的损失函数就是标准化均方误差(NMSE,normalized mean squared error)损失函数。与分类问题的预测不同,回归问题完成的是对具体数值的预测,解决回归问题的网络模型在完成预测之后不会输出一个概率分布向量,而是一个经过模型预测得到的数值。
下面我们关于波士顿住房数据(BostonHousing)的决策树和线性回归的损失函数NMSE1和NMSE2,代码如下:
>>>import numpy as np
>>>import pandas as pd
>>>u=pd.read_csv("BostonHousing.csv")
#导入数据,设置x和y
>>>un0=u.columns
>>>un=un0[5:]复制
#不选前面不参与建模的5个变量
>>>y=np.array(u[un[0]])复制
[:,np.newaxis]#转换成列向量
>>>x=np.array(u[un[1:]])
>>>print(un[0]);print(un[1:])复制
上面的代码实现了数据的导入(在公众号回复“数据”,即可获得本例BostonHousing数据文件),并选用cmedv(自住房屋房价中位数)作为因变量,而其他多数变量作为自变量,由于哑元变量chas(有关查尔斯河的虚拟变量,挨河为1,否则为0)只有两个水平,对回归没有影响,这里不作处理。
#决策树回归和线性回归
>>>from sklearn.tree import复制
DecisionTreeRegressor
>>>from sklearn import linear_model
>>>tree= DecisionTreeRegressor复制
(max_depth=4,random_state=1010)
>>>tree=tree.fit(x,y)
>>>regr=linear_model.LinearRegression复制
(fit_intercept=False)
>>>regr=regr.fit(x,y)
#print(regr.coef_)线性回归的解释变量系数
>>>yp1=np.array(tree.predict(x))复制
[:,np.newaxis]
>>>yp2=x.dot(regr.coef_.reshape复制
(13,1))
复制
以上代码我们实现了波士顿住房数据的决策树回归和线性回归,下面我们根据损失函数计算各自的标准化均方误差。
>>>nmse1=np.sum((y-yp1)**2)/复制
np.sum((y-np.mean(y))**2)
>>>nmse2=np.sum((y-yp2)**2)/复制
np.sum((y-np.mean(y))**2)
>>>print("NMSE1:{:.3}\tNMSE2:{:.3}".复制
format(nmse1, nmse2))
NMSE1:0.111 NMSE2:0.282复制
可以得到决策树回归的标准均方误差为0.111,线性回归的为0.282,并且二者均介于0~1之间,从标准化均方误差来看我们的模型是有效的,而且决策树回归要优于线性回归。
思考
决策树回归和线性回归有哪些区别呢?

理解编程语言,探索数据奥秘
每日练习|干货分享|新闻资讯|公益平台。
每天学习一点点,你将会见到全新的自己。

长按识别二维码关注






