支持向量机理论基础

支持向量机（SVM）是在统计学习理论的VC维理论和结构风险最小化原理基础上发展起来的一种非常经典的机器学习方法。它具有理论严密、适应性强、全局优化、训练效率高且泛化性能好等优点，可非常成功地处理机器学习分类和回归问题。本文先介绍它所基于的这两个理论基础。

 我们知道想要知道总体的真实分布是很难的，应该说是不可能的，因此只能从总体中抽取样本，通过计算样本分布来作为总体的近似模型或经验模型。但是，经验模型毕竟不是真实模型，二者之间是有差距的，为衡量二者之间的差距引入风险的概念。当从训练集得到一个分类器之后，这个分类器是以经验模型的分布作为总体分布的，那么这个分类器的误差就称为经验风险。因为机器学习的算法较多，为了综合评估的方便，将这些误差函数命名为损失函数（Loss Function）。数学表示如下：

神经网络的主要思想在于把经验风险最小化作为衡量算法准确性的主要依据。通过迭代这个误差函数使之收敛到尽可能小的范围之内，或者说达到平稳状态，以此使算法收敛到最优。但是，只求损失函数最小化并不总能达到全局最优的分类效果。经常会出现过拟合的情况，原因有二：一是训练样本对总体的代表性不强，也就是最小的经验风险并不一定意味着最小的真实（总体）风险。这样一来就要求有足够多的样本，但在现实中，还要看问题的特征和设计者的技巧，所以第二代神经网络最后成了建模技巧的比拼，这导致了所建模型逐渐失去了泛化能力。二是说明学习算法理论还不完备，即现有的、单一的经验风险最小（ERM）理论存在着很大的不足。

认识到这个问题，人们将目光转向统计学，希望找到一种方法能衡量样本规律与总体规律之间的差距，也就是所谓的一致性问题。

 从学习一致性的角度来看，当样本数目趋近于无穷大时（大数定理），最小经验风险一定能够收敛于最小真实风险，只有满足这一条件，才能保证在经验风险最小化下取得的最优结果能够代表真实风险的最优结果，如下图1.1所示。

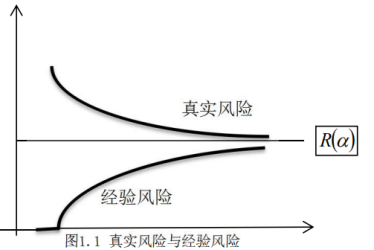
进一步，Vapnik给出了学习理论的关键定理。

由于这个定理在统计学理论中的重要性，因而被称为关键定理。关键定理把学习一致性的问题巧妙地转化为了一个收敛问题：它没有用经验风险去逼近真实（期望）风险（前面说过，这很难），而是通过经验风险最小化函数逼近真实（期望）风险最小化函数，这样，在经验风险和真实风险之间就建起了一座桥梁，即经验风险最小化原则符合学习一致性的条件是Q（z, a)函数集中最差的那个函数。

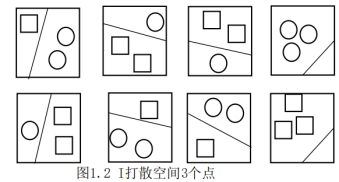
再看4个点的情况，如图1.3。

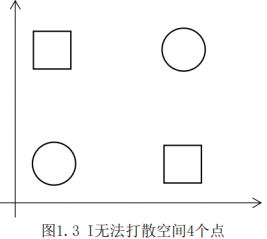
显然无法将4个点分隔，故该指示函数集的VC维就是3。

VC维为线性可分与非线性可分的衡量提供了新的衡量依据。一个数据集是线性可分的，它的维度就是样本空间的维度d；若是线性不可分的，对于线性分类器（含指示函数），它的维度至少等于其VC维h=d+1。因此，函数集的VC维越大，其非线性程度越高，学习机器越复杂。但是，目前除了某些特定函数还没有通用的方法确定所有学习机器的VC维，例如，非线性神经网络的VC维都很难确定。

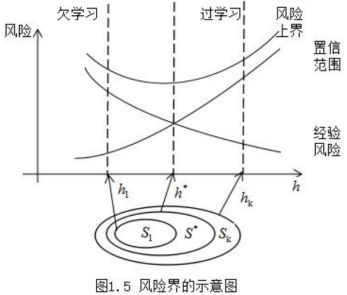
另一方面，对于某类特定问题，固定n的大小，VC维越高，学习机器的复杂性就越高，置信区间越大，经验风险逼近真实风险有较大的误差。所以在设计学习机器时，不但要使经验风险最小化，还要使VC尽量小，从而缩小置信区间，使实际风险最小。本质上，对于神经网络，我们选择学习模型和设计网络的过程就是优化置信区间的过程。

有了推广能力界的概念，我们就可以凭此寻找解决策略，如图1.4。

这样在同一个子集中置信区间相同（因为有相同的VC维和样本量n），可以在每一个子集中寻找最小经验风险。选择最小化经验风险与置信区间之和最小的子集，就可以达到期望风险的最小。这个子集中使经验风险最小的函数就是所要求的最优函数。这种思想称作结构风险最小化原则（Structure Risk Minimization），简称SRM原则。