对于一份图像数据集,在送入模型之前,往往需要做些预处理操作,标准化便是常用的一种预处理操作,它往往能够加速模型的收敛。
标准化公式为:
其中,是原数据集,和分别代表原数据的均值和标准差。
从表格数据的标准化说起
对于表格数据,只需分别计算每列的均值和标准差即可。举个栗子,假设某数据集X如下:
| . | X_feature1 | X_feature2 |
|---|---|---|
| 样本1 | 1 | 30 |
| 样本2 | 1.5 | 45 |
| 样本3 | 0.9 | 35 |
则:
第一个特征的均值为
第二个特征的均值为
第一个特征的标准差为
第二个特征的标准差为
于是,该数据集的均值为,标准差为
标准化的操作如下:
比如对于,其值为,那么,,,于是标准化后的,对于同理可计算。
完整计算得到标准化后的数据为:
| . | X_feature1 | X_feature2 |
|---|---|---|
| 样本1 | -0.5068 | -1.06 |
| 样本2 | 1.398 | 1.33 |
| 样本3 | -0.8879 | -0.26 |
不妨用sklearn来验证下计算结果的准确性: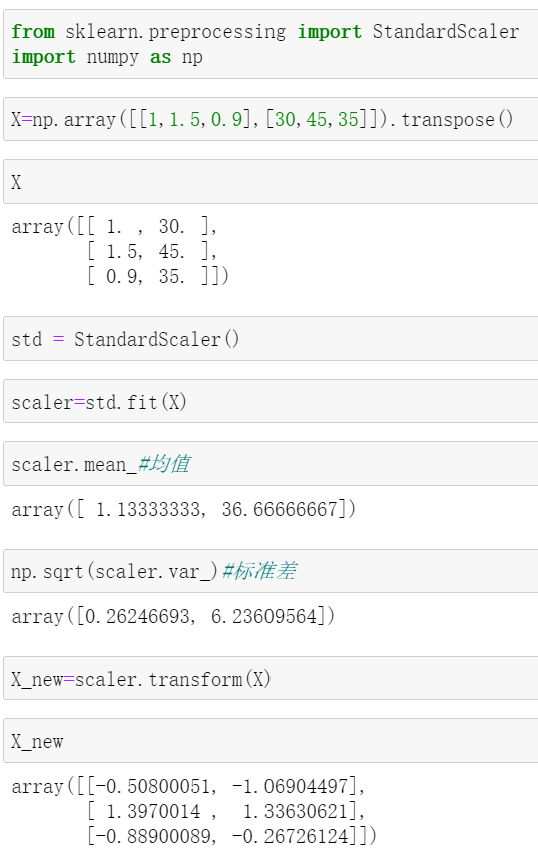
除去舍入误差,结果是一致的。
对图像数据进行标准化
现在,我们加大难度,对具有更高维度的图像数据进行标准化。
首先自定义一份图像数据集:
class MyDataset(Dataset):
def __init__(self,path='my_images'):
super().__init__()
self.path=path
all_imgs=os.listdir(path)#获取全部图片的名字
self.imgs = []
#将每张图片的所在路径读取进来,保存在self.imgs中
for img_name in all_imgs:
image_path = os.path.join(self.path,img_name)
self.imgs.append(image_path)
def __len__(self):
return len(self.imgs)
def __getitem__(self, index):
image=Image.open(self.imgs[index]).convert('RGB')#读进去是RGBA,需要转换一下
image=np.array(image)#将PIL图像转成数值
image = np.array(image).astype(np.float32).transpose((2, 0, 1))#image是HWC的,这里转为CHW
return image
dataset=MyDataset()
dataloader=DataLoader(dataset, batch_size=4, shuffle=True)复制
制作好数据集后,可以打印看一下:
可以看到,数据集中的图像尺寸为256*256
,并且已经将图片的格式转为PyTorch要求的格式:CHW
.
准备好数据集之后,就可以准备计算整个数据集的均值和标准差了。需要明确的是,我们是分别对每个通道上的“单张图”进行均值和标准差的计算的。这里"单张图"可能描述不太严谨,举个例子吧,比如一张图片的shape为[3,256,256],那么将dim0,也就是通道维度做切分,可以得到3个256*256
的矩阵,其中的每一个矩阵便是上面所说的"单张图"。
对于均值,直接对每个"单张图"的像素求和,再除以总的像素点个数即可 ;
对于标准差,它的平方等于方差,因此需要求方差。在之前的表格数据举的栗子中,我们使用了进行求解,而这里将使用另外一个公式,相信学过数理统计的你对它还不算陌生:
现在,就可以写代码啦
def get_mean_std(loader):
channels_sum,channels_squared_sum,num_batches=0,0,0
#这里的data就是image,shape为[batchsize,C,H,W]
for data in loader:
channels_sum+=torch.mean(data.float().div(255),dim=[0,2,3])
#print(channels_sum.shape)#torch.Size([3])
channels_squared_sum+=torch.mean(data.float().div(255)**2,dim=[0,2,3])
#print(channels_squared_sum.shape)#torch.Size([3])
num_batches+=1
#计算E(X),这也就是要求的均值
e_x=channels_sum/num_batches
#计算E(X^2)
e_x_squared=channels_squared_sum/num_batches
#计算var(X)=E(X^2)]-[E(X)]^2
var=e_x_squared-e_x**2
return e_x,var**0.5复制
比较难以理解的,应该是里面的dim=[0,2,3]
。这里推荐一个理解方法:做类比。
在前面对表格数据进行标准化时,我们是对每一个特征(每一列)求解均值和标准差。表格数据是二维的,即"行"与"列"。我们当时的计算是按照"列"进行的,具体表现为对每一行元素进行操作。数据一共有3行,一共有2列,计算得到的均值为,标准差为,它们所含元素的个数和"列"数都是一样的(都是2)。
推广到图像数据,对于每一轮的迭代,数据一共有batchsize个(batchsize张图片),每个图片的shape为[C,H,W],在C表示的通道维度上计算均值和标准差,根据前面的类比,它具体表现为对除了通道(C)维度之外的其他维度元素进行操作,最终计算得到的均值和标准差的个数应该都和C相等。
现在再看dim=[0,2,3]
, 就应该明白了:它对除了第一个维度(通道维度)之外的元素进行操作,具体地,对所有元素求均值。
我们可以手动验证下: 看,两者的结果是一样的。以上便是关于
看,两者的结果是一样的。以上便是关于dim=[0,1,2]
的解释。
代码中还出现了.div(255)
,也就是将图像的每个像素值都除以了255,以便将像素取值归一化到[0,1]区间内。这一操作其实是可选的,具体来说,在PyTorch中,如果你的图像在做标准化之前,已经使用了ToTensor
,那么图像已经自动做了"除以255"这个操作,此时就无需在计算均值和标准差时加上.div(255)
了。
在对每个batch计算完成后,需要将变量值除以总共的batch数(num_batches
),这才是真正意义上的平均。
最后,调用上面写好的get_mean_std
函数,求解均值和方差: 看,它们所含元素个数都是3,和通道数一致。
看,它们所含元素个数都是3,和通道数一致。
有了均值和方差,将它们传入torchvision.transforms.Normalize
就实现了图像的标准化操作。该方法会在通道维度上对每个"单张图"做标准化,正如官方给出的解释:
output[channel]=(input[channel]-mean[channel])/std[channel]复制
参考:
[1] https://www.youtube.com/watch?v=y6IEcEBRZks&list=PLhhyoLH6IjfxeoooqP9rhU3HJIAVAJ3Vz&index=52 [2] https://pytorch.org/vision/stable/transforms.html
重磅!南极Python交流群已成立,添加下方微信,备注加群即可进群。

感谢点赞,分享和在看的你!







