在介绍贝叶斯算法之前,要先明确两个概念
1 联合概率分布
联合概率分布简称联合分布,是两个及以上随机变量组成的随机变量的概率分布。根据随机变量的不同,联合概率分布的表示形式也不同。对于离散型随机变量,联合概率分布可以简单的理解为求和的形式,即对两个变量的概率求其全部的和。对于连续型随机变量,联合概率分布即对这个二维变量的概率函数对这两个变量求积分
离散型:
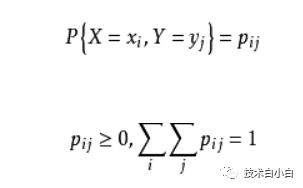
连续型:
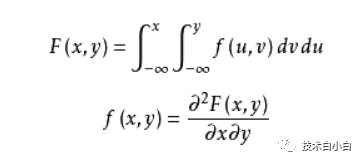
实际应用当中要学会灵活应用
2, 先验概率
先验概率:是指根据以往经验和分析得到的概率
后验概率:事情已经发生,要求这件事情发生的原因是由某个因素引起的可能性的大小
贝叶斯算法
机器学习当中常用的算法名为朴素贝叶斯算法(naive Bayes)原意为天真的贝叶斯,因为概算里面采用了很多的假设信息。
朴素贝叶斯算法的学习与分类
一般的数据集 由如下形式给出
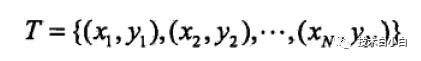
其中x属于n维空间,表示样本x的各个属性,y表示类别,在分类里面表示用数字表示分类标签。
计算朴素贝叶斯分类一般只需要计算三个概率即可
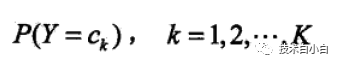
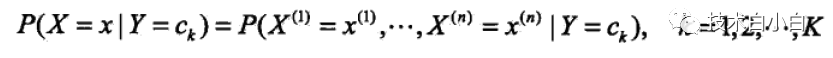
这两个先验概率可以根据实际的数据,很容易计算出来,那么由这两个先验概率,就得到了联合分布概率 P(X, Y),但是其指数是有指数量级的,但是由于我们的很多假设,就将这个模型变简单许多。
该假设就是:假设条件概率分布为条件独立,因此该算法就变得很简单了最终得到如下的公式:
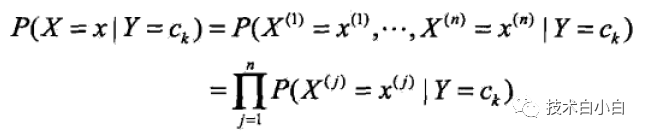 (1)
(1)
 (2)
(2)
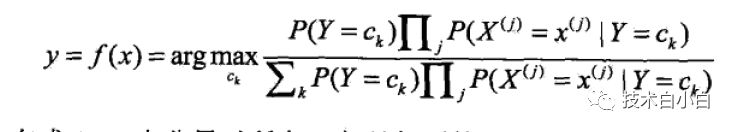 (3)
(3)
最终得到了公式(1)。根据实际给出的训练样本,分别计算Y=Ck1,Ck2,,Ckn时候,X =x1,x2,,xm的概率。将公式(1)代入到公式(2)里面去,就可以得到每个样本对应与每个类别的概率,利用公式(3)取最大值就可以确定每个样本的归属。由于公式(3)的分母部分对于一直的样本属性个数和类别数是确定的,于是公式(3)可以简化。
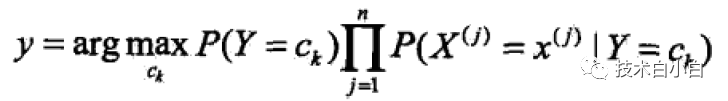 (4)
(4)
该算法的原理可以证明,通过0-1损失函数,计算其期望风险,最小化之后就能得到后验概率的最大化类别,在此不再详述。
朴素贝叶斯的参数估计
前面讲了朴素贝叶斯的原理部分,但是当我们应用于实际的时候,就要将每一部分具体计算出来,这里采用两种方法,将上面公式(4)里面的各个概率计算出来
1.极大似然估计
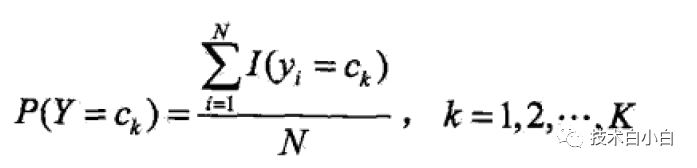 (5)
(5)
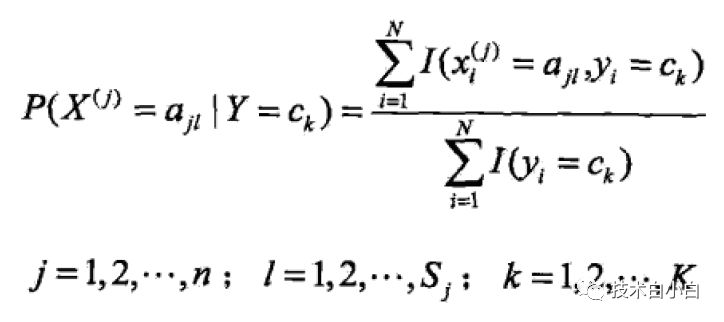 (6)
(6)
其中Xi(j)表示样本i的第j属性的取值,X属于n维,每个属性有Sj个取值可能,k表示样本类别总数
2.贝叶斯估计
为了防止在纪大似然概率当中,出现为0的概率,导致误差偏大,贝叶斯估计对极大似然估计做了一定的改进,即在两个概率当中加入了一个值,防止概率变为0
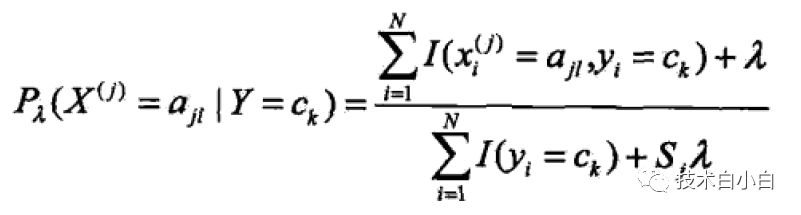

接下来用一个例子来计算,帮助理解
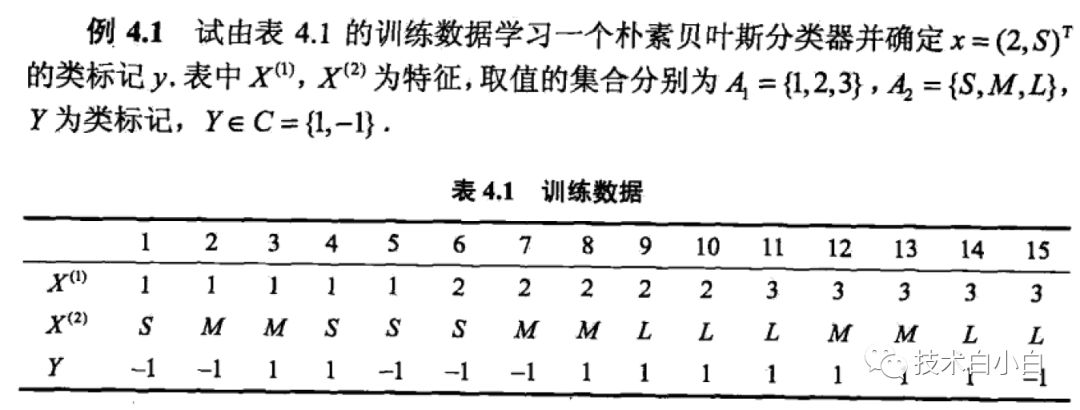
当采用极大似然估计计算的时候,过程如下:
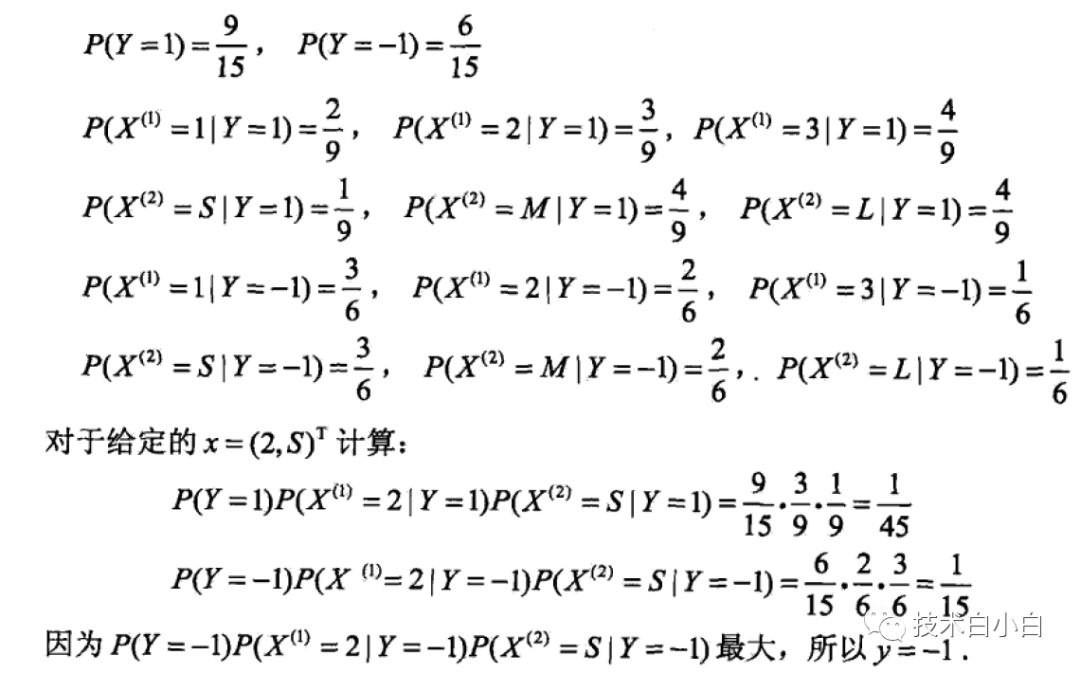
当采用贝叶斯估计时候,计算步骤如下:
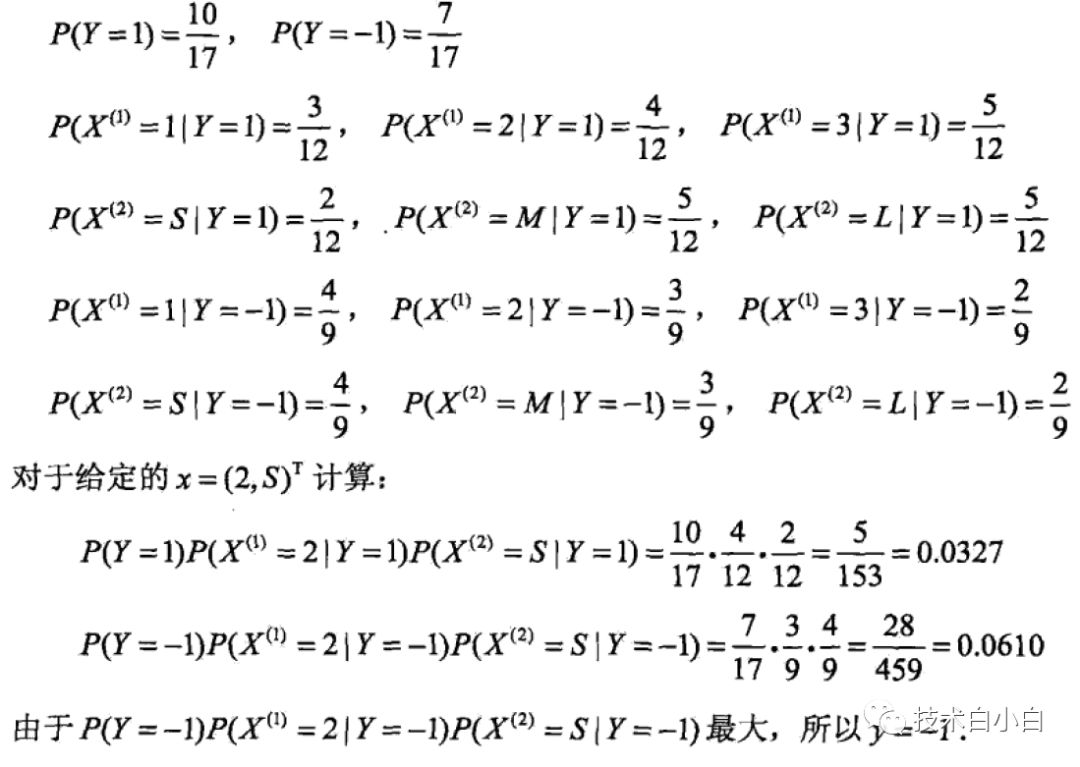
参考:
统计学习原理 李航 第四章 朴素贝叶斯算法






