对于任何接受过中学教育的读者,最熟悉的概率分布莫过于正态分布,它描述了重复多次实验后一个受到随机因素影响的独立变量呈现的概率分布。然而在大脑中,常见的却是有着长尾特征的对数正态分布。
究竟是什么样的生物学机制会产生对数正态分布?大脑又是如何利用这种分布在不同尺度上——从细胞到感知——支持其复杂功能?遵循这一分布模式,大脑的高效运算为人工智能的发展又提供了哪些启示?本文将回顾经典综述和数篇之后的相关研究,试图一一解答这些问题。

正态分布 VS 对数正态分布
什么是对数正态分布?为了理解这个概念,你需要先参与一个虚拟股市的模拟游戏。游戏开始时,每位玩家都有相同的启动资金,玩家需要每天根据市场的随机波动买卖股票。每位玩家的决策和运气将决定他们的盈亏。第一天,玩家的盈亏会遵循一个简单的正态分布,小部分亏了很多,小部分赢了很多,大部分人处于亏一点或赢一点之间。
但随着时间的推移,你会发现,尽管每天的涨跌都是随机的(每次决策的盈亏都会呈现正态分布),最终每个人的资金量却呈现出一种非对称的、长尾的分布——这就是对数正态发布。
因为玩家的资金每次增减都是在之前资金的基础上进行的,这会形成一种累积效应。所以,大部分玩家资金量都会集中在较低的水平(大部分人盈亏均衡,小部分就算一直亏损也只会越亏越少),只有极少部分出现在高值(连续盈利的人很少,但只会越挣越多),形成长尾分布*。
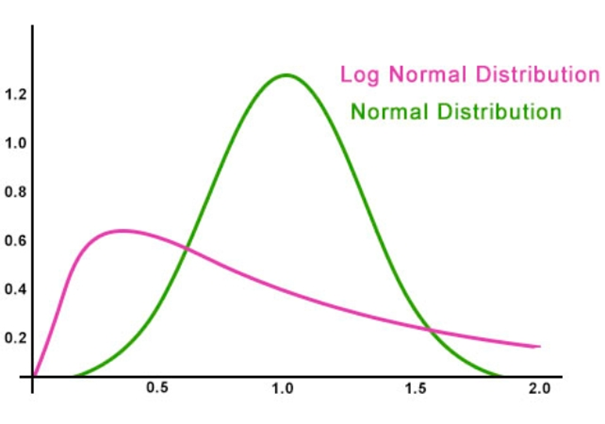
▷图1.正态分布与对数正态分布的对比,绿色:正态分布;红色:对数正态分布。在股市的例子里,横轴为资金,纵轴为数量,在神经元内,横轴为激活频率,纵轴为数量。在股市的例子里,因为玩家的资金每次增减都是在之前资金的基础上进行的,每次交易玩家的资金都有可能增加或减少一个固定百分比(比如增加或减少50%)。那么将会有极少部分人连续亏损,从100到50到25到12.5到6.25;而极少部分人连续盈利,就是从100到150到225到337.5;更多的人是处于或盈或亏中,如100到150到75到112.5到56.25;100到50到75到37.5到56.25,最后大部分人都集中在较低值。
在学术界,对呈现对数正态分布的随机变量,还有诸如幂律(power law),无标度(scale-free)等描述,其背后都指向同一现象。

神经元间的激活间隔、树突棘大小、
神经突触的密度都遵循对数分布
在大脑的世界里,神经元的行为有点像城市中的灯光。大多数时间,大部分灯光是关闭的,但偶尔会有一些灯光亮起来,照亮周围的一小块区域。
已有多项研究表明,这些“点亮”的间隔——也就是神经元的激活频率(firing rate)——遵循对数正态分布的模式[1]。这一规律不仅适用于小鼠,人等各个物种;兴奋性的锥体神经元,抑制性的中间神经元;还适用于从进化上更原始的小脑和执行各种高级认知功能的新皮层中的各个脑区。
由于对数正态分布的不对称特征,这意味着少部分神经元在大脑中经常激活,而剩下的大部分神经元看起来在积极“摸鱼”(时不时激活)。此外,神经元的激活后尖峰的振幅,突触的权重也遵循正态分布[1]。
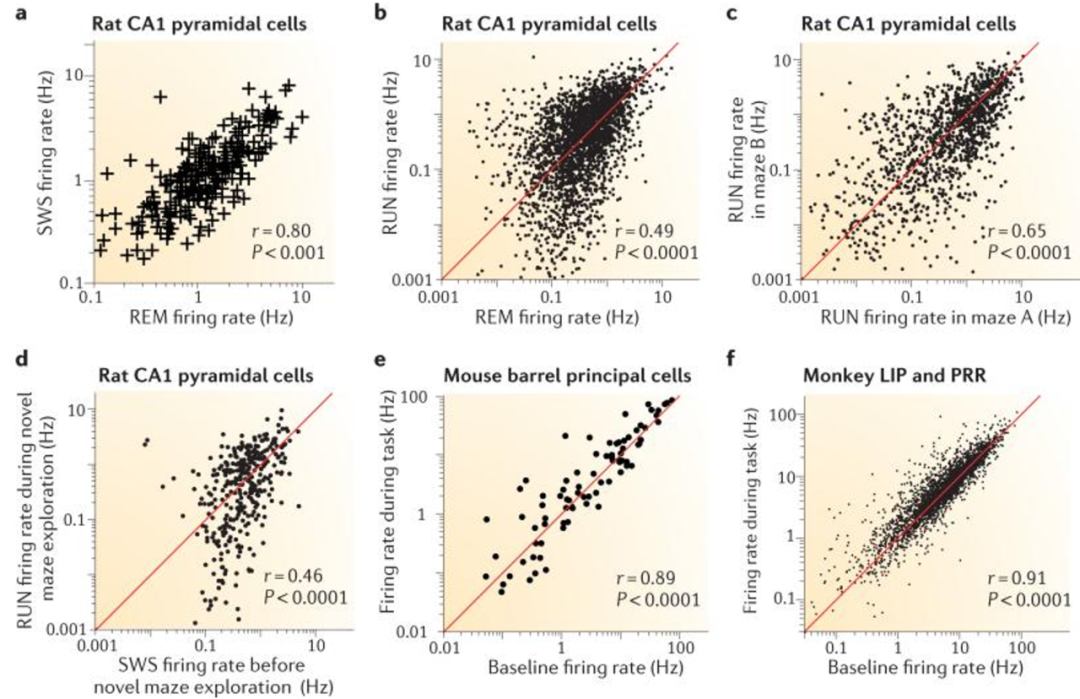
▷图2. 不同脑区和环境下,多种常见神经细胞其激活率都遵循对数正态分布(此处横轴,纵轴都是对数处理后的,因此呈显出线性散点图),参考文献1。
但神经元不只是简单地“开”或“关”。如果我们细看它们的结构,会发现树突分枝上的棘状突起——树突棘(dendritic spine)。一个神经元上可能包含数百个大小不同的树突棘,这些树突棘在神经元的发育过程中会发生变化(可塑性),并承担着信息存储计算等功能。
一项研究观察到,在小鼠的听觉皮层中,这些树突棘的大小也遵循对数正态分布(图4),而且它们的变化幅度与其自身大小成正比,这有点像股市中的资金波动:投入的资本越大,其波动的幅度也越大。
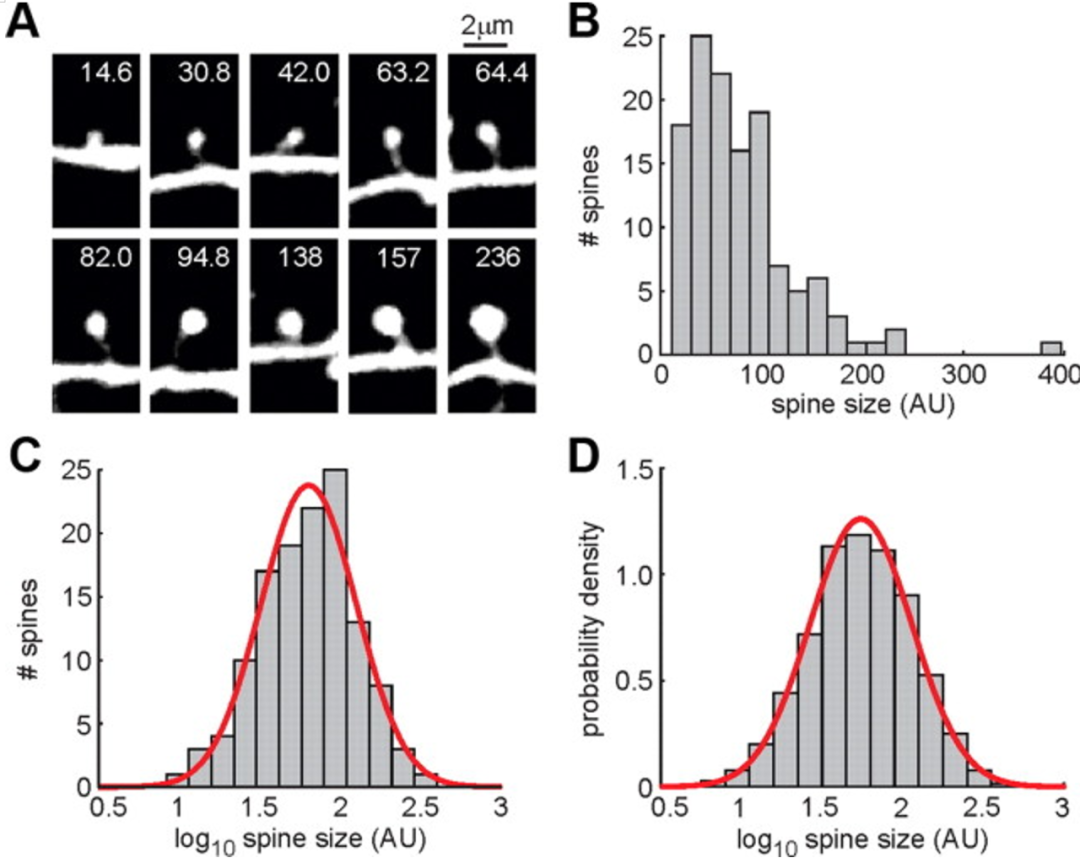
▷图4. 树突棘大小呈对数正态分布。A,树突棘示意图,B,原始概率分布,C,D,X轴经过log转换后的树突棘数目和概率分布。
以上分析来自对单个神经元的记录,但随着连接组技术的进步,研究者能够对特定区域的神经元组成的网络进行映射。比如一项针对9种哺乳动物的研究[3]指出,其中7个物种的大脑皮层中神经元的密度(每立方毫米包含多少个神经元)都呈现出对数正态分布(图5)。这说明了对数正态分布可视为神经系统宏观组织的一项基本规律,也可以成为设计神经形态(neuromorphic)硬件时需要关注的约束。
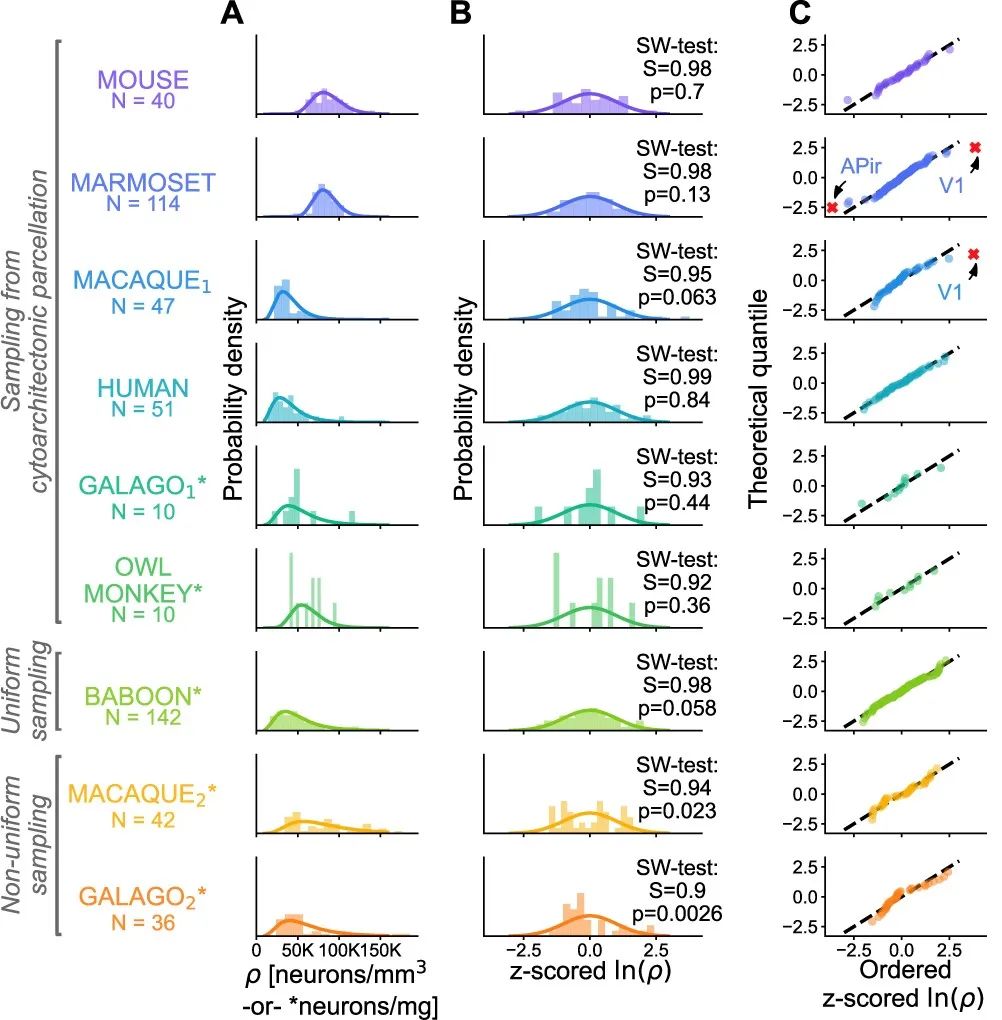
▷图5. 9种哺乳动物神经元密度的分布图,偏移程度的分布图,其中不符合对数正态分布的两个物种(GALAGO和OWL MONKEY),可能的原因是采样点不均,样本数偏少。图源:参考文献3

我们真的只用了百分之十的大脑吗?
民间心理学总是流传我们只使用了大脑的10%,但这种说法源于对大脑活动模式的误解。大脑的活动并不是均匀分布的(正态分布),而是显示出明显的“长尾”特征,即少数神经元非常活跃,而大多数则较少参与活动。对于神经元激活率分布的成因,一般的观点将其归于神经元间的相互连接[1]。
(1)神经元之间的相互作用
让我们借用大型交响乐队的比喻来进一步理解这一点。在大型交响乐队中,每个乐手都有自己的乐器和演奏节奏。在整场演出中,并不是所有乐手都在同一时刻演奏,而是根据乐曲的需要,某些乐手的演奏会非常活跃,形成音乐的高潮,而其他乐手则可能处于休息状态,等待下一个演奏时机。这种非均匀的活动模式,很好地反映了大脑中神经元的激活状态:大多数神经元在大部分时间可能较为“安静”,但每时每刻,不断变化的一小撮活跃神经元推动大脑完成复杂的思维和感知任务。
这种活动模式的科学背景是神经元之间的相互作用不是简单的相加,而是累积式,类似于乐手之间的和谐配合和相互激励,可能涉及到复杂的调节和反馈机制 。比如,在某些情况下,一个神经元的活动可能会促使与它紧密相连的其他神经元也变得活跃,形成一个活动的“热点”,这在整个神经网络中会呈现出对数正态的分布特征。
除了从神经元间的连接模式去解释累积现象外,也有研究基于“整合-发放模型” (Integrate-and-Fire Model)说明,即使是独立的单个神经元,也可能因为内部的累积调整(膜放电受到的误差累乘)而表现出对数正态的激活率[4]。
(2)赫布法则
另一种解释神经系统呈现对数正态分布的模型,来自神经元间遵循赫布法则的自组织[5]。简单来说,就像社交网络中的人际关系,神经元们如果经常在一起(一起激活),那么它们的连接就会更紧密(连接强度增强)。不论是简单的线虫还是复杂的果蝇和小鼠,其神经连接的数量和密度都显示出无标度的长尾特征——即大多数连接比较弱,而少数连接非常强。
上述解释对应模型的理论预测结果,已在真实实验中被验证,通过增强共同激活(包括直接的一阶连接,以及图6a所示的二阶和三阶间接连接)的神经元之间的连接强度,这些模型能够再现真实出现的连接强度分布(图6b中的实线)。这说明了神经系统的模块化源自连接网络的生成机制,而非物种及神经元的特异性,从而进一步解释了为何对数概率分布会如此普遍的出现。
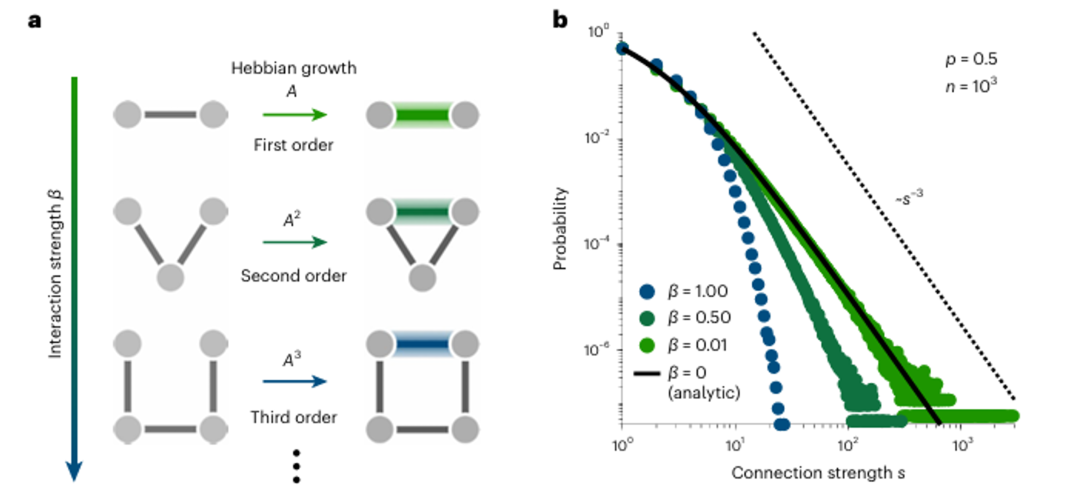
▷图6. 基于赫布法则解释神经活动的无标度性质。
(2)耗能与演化角度
从减少大脑的能量消耗及信号传输距离的角度,对数正态分布是有利的[6],具体来说,是通过让少数神经元聚集在某一区域,形成模块化的“富人俱乐部”,同时少部分神经元频繁激活来实现的。因此,模块化、少量计算单元的频繁激活等应该成为类脑计算应当遵循的设计原则。
而从进化上来讲,一个已准备好的、具有少数密集连接、且快速激活的神经元群体,作为大脑中的骨干连接,可以看成是时刻准备着,能够快速发挥作用的系统,这对物种的生存很有必要。然而,大脑能发挥的全部功能,取决于那些稀疏连接着的、不频繁激活的大多数神经元提供的另一套系统。这些神经元在日常活动中较少参与,但在需要适应新的或不常见的刺激时发挥作用。
因此,我们不该说我们只使用了大脑的十分之一,而应将只有10%的大脑在积极工作,视为生物为了在多个时间尺度应对常见和不常见刺激而采取的最优权衡,是大脑处于临界态(criticality)而呈现的特征[7]。
(4)其他解释
除了上述的模型,另一种解释神经系统中对数正态分布的模型[8],考虑了两种不同类型的神经元。该模型将神经元分为两类,一类接受了过多的“静音”信号(抑制性神经元的影响)而保持沉默,而另一类则因为“音量加大”(兴奋性神经元的影响)而变得非常活跃。这个模型假设所有神经元接收到的初始信号是均匀分布的,就像是从各处均匀而来的声音。但随着这些信号在神经元中的累积影响,那些更多地受到兴奋性影响的神经元会将这些信号放大,导致它们的活动输出呈现出对数正态分布。
这种模型不仅解释了兴奋性和抑制性的平衡如何塑造神经反应,也阐明了神经系统如何保持对微小信号的敏感性,同时避免对过强的输入做出过度反应。
▷图7. 由于非线性增益带来的神经元间对数正态分布。
此外,还有一个由Per Bak在其著作《大自然如何运作》中提出的模型,称为“临界沙堆模型”,提供了另一种视角。在这个模型中,沙粒的积累和崩塌过程类似于神经元网络的动态变化:随着沙堆的累积,小的沙崩是随时会发生的,大的沙崩需要较多的沙子累积,所以较少发生。
科学家们通过研究细胞骨架的物理和机械特性[9],发现神经元的聚集和分裂行为类似于沙堆的崩塌,从而导致神经元密度的分布也呈现出对数正态分布,这解释了神经网络中“少数活跃,多数沉默”的不均匀现象。
▷《大自然如何运作》,Per Bak著。
小结:考察神经系统
呈现的统计特征有什么用?
通过深入分析神经系统的统计特征,研究者们能够揭示跨越不同物种和脑区的一些普遍规律,同时也能探究在不同环境刺激下这些特征如何变化。
例如,一项关于恒河猴的研究发现[10],恒河猴在看到熟悉和陌生的视觉刺激时,大脑中的神经元激活频率都遵循对数正态分布,但不同环境下激活率的统计特征存在差异。相比看到熟悉图片,在看到陌生图片时,神经元激活率分布的长尾特征更明显,方差更大(图8)。这可以视为在看到陌生图片时,神经元的激活更加积极(努力适应新环境中的刺激),而在熟悉环境中则可以利用已构建好的模块。
然而,这项研究只考虑了神经元间的连接,没有考虑神经元上的树突棘同样可以承担存储及计算功能。也许神经系统在面对熟悉的刺激时,选择了使用不那么耗能的树突棘局部改变来保持可塑性,这有待之后的研究证实。类似的研究思路,还可以对比不同脑区神经元密度的概率分布是否存在差异,并从发育时的细胞骨架的机械/遗传/基因表达等上对可能的差异加以解释。
▷图8. 恒河猴神经元面对熟悉和陌生刺激时的激活率的理论和真实概率分布。
对于神经系统呈现的对数正态分布,有一个形象的描述:神经元雪崩,即神经活动会出现持续几十毫秒的短暂爆发,之后是几秒钟的静止期。神经元雪崩对信息的存储,传输,计算能力,稀疏性及稳定性都很密切相关,是从事类脑计算时需要考虑的基本限制因素之一。例如“千脑计划”提出的皮质柱计算,其模拟大脑时能否让其模型也呈现出类似本文描述的对数正态分布,是判断其成功与否的标准之一。
对于神经系统的各类对数正态分布的生成机制,已有多种基于不同假设的模型能拟合真实数据,对其进行解释。很有可能的是,各个模型分别抓住了真实中神经系统的某个侧面,但真正的神经活动模式可能是这些机制的综合效果。
从更大的视角来看,神经系统表现出的对数正态分布反映了其内在的异质性,并且是大脑进行鲁棒学习和低能耗计算的基础。虽然“幂律”、“无标度”、“神经元雪崩”等术语各自描绘了这些现象的不同侧面,但它们本质上描述的是同一个复杂的生物逻辑。本文只在概述相关研究,对这些主题感兴趣的读者可以进一步细读参考文献1。
正如我们通过股市模拟游戏看到的那样,大脑的工作模式与我们日常生活中的许多现象惊人相似,都遵循某些基本的数学规律。从单个神经元的微观反应到整个神经网络的宏观动态,大脑都在使用对数正态分布来优化信息处理、节省能量并增强其对外部世界的适应性。这种分布的数学本质促使我们发问,自组织过程产生的长尾分布,神经元雪崩等现象,是否能够在人工神经网络中发现?Transformer中的概念激活率是否也遵循对数正态分布?
[1] Buzsáki, G., & Mizuseki, K. (2014). The log-dynamic brain: how skewed distributions affect network operations. Nature Reviews Neuroscience, 15(4), 264–278. https://doi.org/10.1038/nrn3687
[2] Loewenstein, Y., Kuras, A., & Rumpel, S. (2011). Multiplicative Dynamics Underlie the Emergence of the Log-Normal Distribution of Spine Sizes in the Neocortex In Vivo. Journal of Neuroscience, 31(26), 9481–9488. https://doi.org/10.1523/jneurosci.6130-10.2011
[3] Aitor Morales-Gregorio, Alexander van Meegen, & Sacha. (2023). Ubiquitous lognormal distribution of neuron densities in mammalian cerebral cortex. Cerebral Cortex, 33(16), 9439–9449. https://doi.org/10.1093/cercor/bhad160
[4] Kish, E. A., Granqvist, C.-G., Dér, A., & Kish, L. B. (2015). Lognormal distribution of firing time and rate from a single neuron? Cognitive Neurodynamics, 9(4), 459–462. https://doi.org/10.1007/s11571-015-9332-6
[5] Lynn, C. W., Holmes, C. M., & Palmer, S. E. (2024). Heavy-tailed neuronal connectivity arises from Hebbian self-organization. Nature Physics, 1–8. https://doi.org/10.1038/s41567-023-02332-9
[6] Bullmore, E., & Sporns, O. (2012). The economy of brain network organization. Nature Reviews Neuroscience, 13(5), 336–349. https://doi.org/10.1038/nrn3214
[7] Robinson, P. A., Gao, X., & Han, Y. (2021). Relationships between lognormal distributions of neural properties, activity, criticality, and connectivity. Biological Cybernetics, 115(2), 121–130. https://doi.org/10.1007/s00422-021-00871-z
[8] Berg, R. W. (2017). Neuronal Population Activity in Spinal Motor Circuits: Greater Than the Sum of Its Parts. Frontiers in Neural Circuits, 11. https://doi.org/10.3389/fncir.2017.00103
[9] Polizzi, S., Arneodo, A., Pérez-Reche, F.-J., & Argoul, F. (2021). Emergence of Log-Normal Type Distributions in Avalanche Processes in Living Systems: A Network Model. Frontiers in Applied Mathematics and Statistics. https://doi.org/10.3389/fams.2020.613962
[10] Lim, S., McKee, J. L., Woloszyn, L., Amit, Y., Freedman, D. J., Sheinberg, D. L., & Brunel, N. (2015). Inferring learning rules from distributions of firing rates in cortical neurons. Nature Neuroscience, 18(12), 1804–1810. https://doi.org/10.1038/nn.4158
关于追问nextquestion
天桥脑科学研究院旗下科学媒体,旨在以科学追问为纽带,深入探究人工智能与人类智能相互融合与促进,不断探索科学的边界。如果您有进一步想要讨论的内容,欢迎评论区留言,或扫二维码添加小助手微信questionlab,加入社群与我们互动。

关于天桥脑科学研究院
天桥脑科学研究院(Tianqiao and Chrissy Chen Institute, TCCl)是由陈天桥、雒芊芊夫妇出资10亿美元创建的全球最大私人脑科学研究机构之一,总部设在美国。
TCCI与华山医院、上海市精神卫生中心设立了应用神经技术前沿实验室、人工智能与精神健康前沿实验室;与加州理工学院合作成立了TCCI加州理工神经科学研究院。
TCCI建成了支持脑科学研究的生态系统,项目遍布欧美、亚洲和大洋洲,包括学术会议和交流、夏校培训、AI加速科学大奖、科研型临床医生奖励计划、特殊病例社区、中文媒体追问等。

- JackieZhai北京2天前似乎参考文献没列全?追问nextquestion作者2天前7这个是应该滑动组块,向下滑动就有后面的参考文献了。
- 天湖北昨天2对数正态分布似乎也适用于部分材料的强度模型。天湖北昨天2是不是财富分配的2/8原则也是对数正态分布的实例?追问nextquestion作者昨天3在形态上类似,都呈现长尾特征,但在数学定义和形成机制上是有区别的。
- 邹浙江昨天1模拟信号的量化在强度较小的地方量化比较密集,在强度大的地方量化稀疏,可能也是类似的道理
- 随风湖北昨天1纯属胡说八道
- Joseph-Lau辽宁2天前1
![[强]](https://oss-emcsprod-public.modb.pro/image/editor/20240719-87a0ba78-da08-4583-9490-2b6ba7c78332.png)
![[强]](https://oss-emcsprod-public.modb.pro/image/editor/20240719-7bc76afa-7a31-4c19-9722-d8ae011a5e13.png)
![[强]](https://oss-emcsprod-public.modb.pro/image/editor/20240719-82523299-a86a-4923-b3e6-784facdffd8b.png)
- 马卡龙专用可可酱福建3小时前此时不妨追思一下孟德尔,通过数学形式的漂亮拟合,或许我们已经可以大胆地猜测神经元通过自组织以实现预测或表征拟合功能的简单原理了。 比如采用赫布法则的逻辑,考虑到大脑皮层的多层细胞组织模式,我们似乎可以构想一种通过“兴奋—抑制交替环路”的细胞支路异相信号闭环。通过交替排列正反馈和负反馈的逻辑程序,取某个作为观测枢纽的节点细胞,其实很容易就能表现出在常态下的对数正态分布模式。 而至于高激活度的表征中心,无论是外界信息应激诱发的,还是通过自由联想凭借原有神经细胞网络的链接权重分布“自发”的,其实都是对应着更“非随机”的路径诱导模式。但是在宏观的系统中,这种局域的“非随机”高激活度依然是可以被热力学“随机”粒子演化反应统筹在一个更大的玻尔兹曼温标概率分布背景之内的。在这种情况下,其实对数正态分布的模式依然可以存在。只是就像遇到新鲜刺激的猴子一样,这种时候系统处于更高的功率状态,激活度的绝对差将进一步扩大,并在宏观上展现出一种更有序的同步化模式。 甚至可以更大胆一点,认为那些高激活度的“权重热点”就是我们实现“注意力表征”的方式,即“注意”现象其实只是一个神经自组织网络的数学属性的表象而已。 如此其实我们可以合理预言,由于自组织系统演化弛豫的存在,不同高激活度“热点”的产生和消失肯定有不可避免的时间差。其实一些中午激情电竞下午考试爆炸的学生应该对这个过程机制深有体会
![[旺柴]](https://oss-emcsprod-public.modb.pro/image/editor/20240719-92a20bc0-625f-4756-abf2-e39432668fbd.png)

- JackieZhai北京2天前似乎参考文献没列全?追问nextquestion作者2天前7这个是应该滑动组块,向下滑动就有后面的参考文献了。
- 天湖北昨天2对数正态分布似乎也适用于部分材料的强度模型。天湖北昨天2是不是财富分配的2/8原则也是对数正态分布的实例?追问nextquestion作者昨天3在形态上类似,都呈现长尾特征,但在数学定义和形成机制上是有区别的。
- 邹浙江昨天1模拟信号的量化在强度较小的地方量化比较密集,在强度大的地方量化稀疏,可能也是类似的道理
- 随风湖北昨天1纯属胡说八道
- Joseph-Lau辽宁2天前1
![[强]](https://oss-emcsprod-public.modb.pro/image/editor/20240719-70e86a94-a8fc-46fd-afef-d324ff7f63d2.png)
![[强]](https://oss-emcsprod-public.modb.pro/image/editor/20240719-edb1ca32-9cb9-407b-93af-94c0ecec360e.png)
![[强]](https://oss-emcsprod-public.modb.pro/image/editor/20240719-0bb19383-27a6-42b8-a980-86e8116cd72e.png)
- 马卡龙专用可可酱福建3小时前此时不妨追思一下孟德尔,通过数学形式的漂亮拟合,或许我们已经可以大胆地猜测神经元通过自组织以实现预测或表征拟合功能的简单原理了。 比如采用赫布法则的逻辑,考虑到大脑皮层的多层细胞组织模式,我们似乎可以构想一种通过“兴奋—抑制交替环路”的细胞支路异相信号闭环。通过交替排列正反馈和负反馈的逻辑程序,取某个作为观测枢纽的节点细胞,其实很容易就能表现出在常态下的对数正态分布模式。 而至于高激活度的表征中心,无论是外界信息应激诱发的,还是通过自由联想凭借原有神经细胞网络的链接权重分布“自发”的,其实都是对应着更“非随机”的路径诱导模式。但是在宏观的系统中,这种局域的“非随机”高激活度依然是可以被热力学“随机”粒子演化反应统筹在一个更大的玻尔兹曼温标概率分布背景之内的。在这种情况下,其实对数正态分布的模式依然可以存在。只是就像遇到新鲜刺激的猴子一样,这种时候系统处于更高的功率状态,激活度的绝对差将进一步扩大,并在宏观上展现出一种更有序的同步化模式。 甚至可以更大胆一点,认为那些高激活度的“权重热点”就是我们实现“注意力表征”的方式,即“注意”现象其实只是一个神经自组织网络的数学属性的表象而已。 如此其实我们可以合理预言,由于自组织系统演化弛豫的存在,不同高激活度“热点”的产生和消失肯定有不可避免的时间差。其实一些中午激情电竞下午考试爆炸的学生应该对这个过程机制深有体会
![[旺柴]](https://oss-emcsprod-public.modb.pro/image/editor/20240719-77c4b0e1-d5b1-4137-8542-23d420646b26.png)
人划线
评论
 点赞
点赞









