数据结构

本文从二叉树开始到B*树简单讲讲其特点以及优缺点，初步了解一下各种树结构。

二叉树

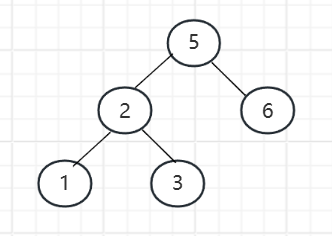
二叉搜索树英文名BST，其是大多数结构的基础，多个领域和产品中都有广泛应用，其不管是插入还是查找某个元素，平均时间复杂度都是O(logn)

特点

每个节点左边的元素都比它小，右边的节点都比它大

它的子树也分别是一个二叉树

缺点

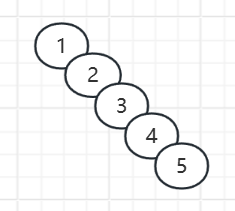
如果插入的数据是有序的，就会成为链表，时间复杂度就会变成O(n)

比如1,2,3,4,5

平衡二叉树

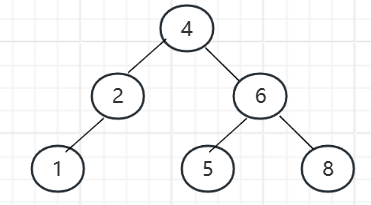
平衡二叉树称为AVL，多了一个旋转的功能，它在插入和删除节点的时候，会根据需要进行左旋或者右旋，来保证二叉树的平衡，就是为了解决二叉树在极端情况下成为链表。

特点：

它的左右两个子树的高度差不会超过1，也就是说偶数情况下左右两个子树就是等高的。

它的子树也分别是一个平衡二叉树。

缺点：

为了维持平衡，其旋转是非常耗时的。特别是在删除操作较多时，维护平衡所需的代价就会很高。

场景：

Windows的进程地址空间管理使用了AVL树

二三树

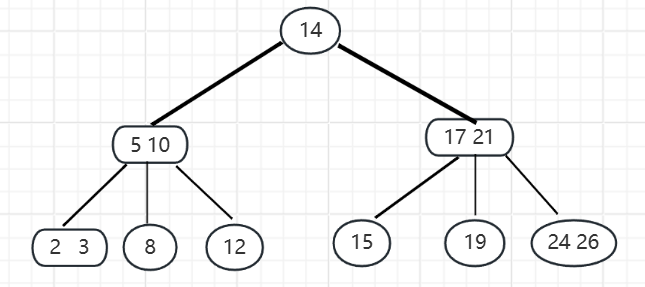
2-3树是一棵绝对平衡的树，即从根节点到任意一个叶子节点所经过的节点数都相同。可以保证每次插入和删除节点时，只需要局部调整即可保证整棵树的平衡，所以其插入和删除的效率上要比平衡二叉树好一些。

特点：

如果一个内部节点拥有一个数据元素、两个子节点，则此节点为2节点。

如果一个内部节点拥有两个数据元素、三个子节点，则此节点为3节点。

每个节点的左边节点的值都比自己小，右边都比自己大

3节点的两个值中间的元素们都位于中间子树下面

缺点：

因为有多种不同的节点，因此代码实现上会有些复杂。使用场景不多，但是二三树的变种红黑树应用领域就非常多了。

红黑树

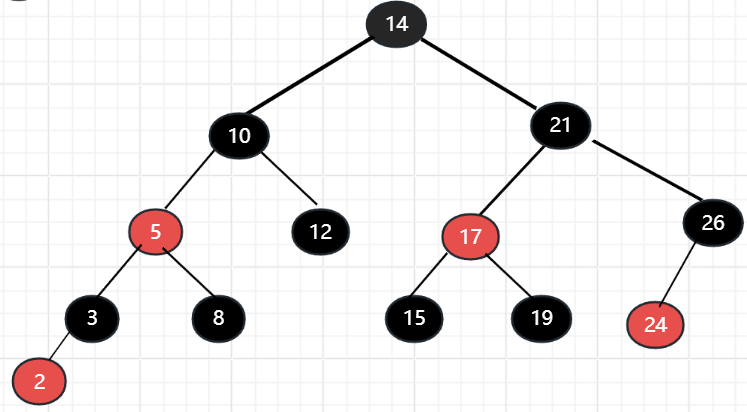
红黑树的查找，插入和删除操作，时间复杂度都是O(logN)。它是从二三树转变过来的，2节点转变为黑色节点，3节点转变为一黑色节点+一红色节点。以上图的二三树为例

特点：

根节点和叶子节点是黑色的

如果一个节点是红色的，那么它的子节点一定是黑色的，因为红节点和其父节点加起来是二三树的一个3节点。

从任意一个节点到叶子节点经过的黑色节点都是一样的。

缺点：

红黑树毕竟是一种二叉树，有着所有二叉树的缺点，就是高度问题，当数据量很大时，树的高度会变得很大，查找时经过的节点过多，效率变低。

另外红黑树在内存表现优秀，但是磁盘中，因为高度原因，会导致数据在磁盘中分散，IO次数过多，效率低下，B树就很好了解决这个问题。

使用场景：

Java中的TreeMap

linux内核，被用于多种管理任务，管理文件描述符等。

在epoll系统中

Nginx流量监控中

B树

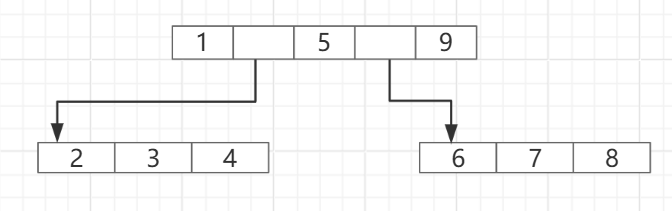
B树分为B-树、B+树、B*树。B-树就是B树，千万不要读成B减树。B树是一种多路搜索树。B树是天生为磁盘而生的，磁盘上的随机查找速度很慢，如果二叉树的高度有十几层，那么查找数据就需要转动磁盘十几次，这种查询效率是很慢的。下图就是一个B树它是一个“矮胖子”。

特点：

每个节点都存储数据以及指向子树的指针

节点中的关键字按照升序排列。

根节点至少有两个子节点

非叶子节点至少包含m/2个子节点，m为层数。

所有叶子节点都是同一个层级中。

其适合一般的动态数据集的存储和检索，插入和删除操作相对均衡。

缺点：

B树的每个节点都存储了键值以及指向子节点的指针，因此在插入或删除数据时可能会破坏其平衡性，需要进行分裂、合并和转移等操作以保持平衡。

B树的内部节点也存储数据，导致空间浪费。

不适合范围查询，由于数据分布在不同层次的节点，可能需要在不同层次节点之间频繁切换访问，导致性能相对较低。

场景：

常用于关系型数据库的索引，比如MongoDB 4.2以前。GIS数据库

在文件系统中用于管理目录和文件，比如 Unix 文件系统中的索引节点（Inode）就是以 B-树为基础结构实现的。

B+树

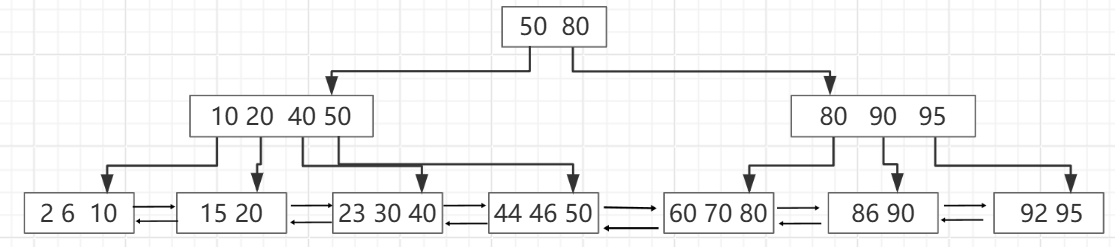
B+树是B树的一种变体，主要区别就是数据都存储到叶子节点，非叶子节点仅存储索引和指针，这样设计的好处就是节点存放的信息量就大大的增加了，树层的高度就基本能控制在四层以内。比如一个页的大小为16k，指针6个字节，索引8个字节，一个根节点就能存储16*1024/(6+8)=1170个索引+指针，假设一条记录时1kb，一个页就能存16条记录，两层树就能存储1170*16=18720条记录。三层树的根节点有1170个，说明中间层也会有1170个节点，每个节点1170个指针，那么3层树就能存储1170*1170*16=21902400条记录，那么4层树就能存储1170*1170*1170*16，得出256亿多的数据。

那么可以看出影响树的高度一是数据量一是索引大小。所以一般不想索引树从三层变成四层，那么超过千万就要考虑分表；索引这边一般也会告诉你索引的字段不要过大，int类型的索引和long型的索引，树的高度都会有影响的。

特点：

非叶子节点，一个索引对应一个指针。

叶子结点之间会有个双向指针连接在一起。

非叶子节点不存储数据，所有数据存储在叶子结点中，所以有更好的缓存命中率，以及降低了I/O操作次数，从而提高查询性能。

所有的索引都会出现在叶子节点的链表中，并且是有序的，所以更适合频繁的范围查询和顺序访问。

了解了B+树，你就会明白工作中，为什么索引有最左前缀原则，为什么DBA会告诉你字段类型设置的够用就好。

缺点：

更新的时候，维护树结构的开销会比较大一些。

在插入或删除操作时，可能会需要页的分裂或合并

访问所有数据需要访问到叶子节点。

应用场景：

广泛应用于关系型数据库的索引，如MySQL、Oracle和SQL Server。

B*树

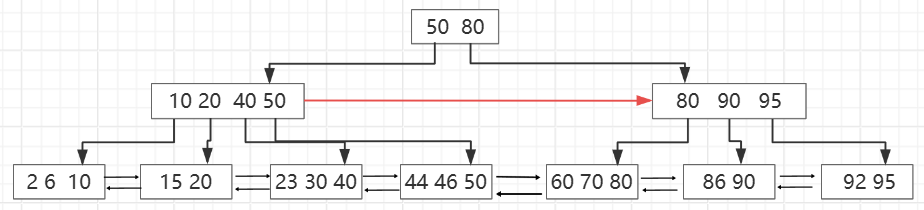
B*树是B+树的变形，在B+树的非根和非叶子节点再增加指向兄弟节点的指针。其目的是减少B+树节点的分裂和合并操作，以提高性能和降低维护成本。

相对于B+树，B*树是一棵更丰满的，空间利用率更高的B+树。

它是如何做的呢？当一个节点满了时，插入一条数据，如果它的下一个节点还有空间，那么会将一部分数据移到相邻节点中，然后修改相对应的父节点和相邻节点的索引指针。

如果相邻节点也满了，则在它们之间增加一个新节点，并各复制1/3的数据到新结点。

特点：

非叶子节点的关键字个数更多

对于节点的分裂和合并的策略有所调整。

缺点：

实现相对复杂。需要更多的代码来处理节点的分裂和合并

应用场景：

听说达梦数据库用了B*树，官方也没有给出说明，除了dm目前还没有听说有哪款产品用的B*树作为其核心数据结构。