王康 https://catkang.github.io/2025/03/03/mysql-btree.html
B+Tree的数据组织
B+Tree是很基础的数据结构,但通常在学术上讨论的时候为了简化,树上维护的数据项都会限定为简单的定长Key Value,这使得实现上对数据的访问,以及判断否需要分裂或合并等操作都非常容易,但对面向现实需求的存储引擎InnoDB来说,这样显然是不够的,再加上上面所讲到的并发控制、故障恢复的需要,InnoDB中的B+Tree数据组织上会显得复杂不少。
B+Tree中的数据项:Record
前面讲到,InnoDB中用B+Tree来维护数据,对数据库来说就是一行行表内容。当用户创建一张表的时候,会在SQL语句中指定这张表中的每一行包含那些列,每一列的类型和长度,是否可以为Null,这些信息都会记录在MySQL的数据字典(Data Dictionary)中,本文不对这里展开讲述,这里只需要知道,数据字典的些列及列长信息,会在对InnoDB的B+Tree进行写入或者读取的时候,通过dict_index_t的数据结构传递下来,并以这个格式进行每一行数据Record的序列化及反序列化,这里只介绍5.1后已经默认的Compact记录格式,以聚簇索引中记录的完整Record为例,一行用户数据序列化后会维护成如下格式:
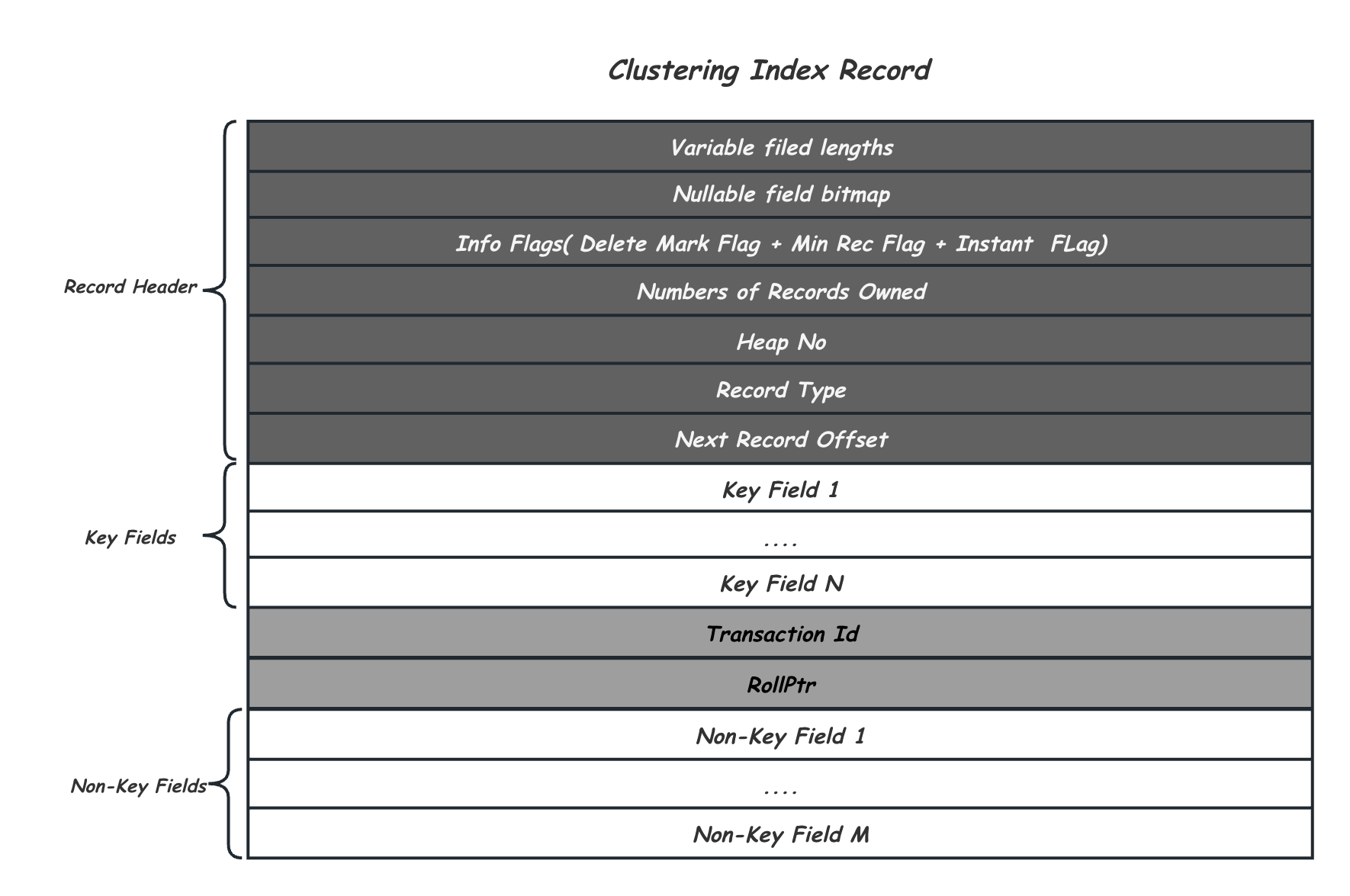
可以看到,其中包括Key字段以及Non-Key字段,之所以这里Key也会有多个,是因为可能有组合索引的情况,事务ID及Rollptr作用在上面介绍过,用来对读提供MVCC访问。除此之外,还有一个Record Header,其中记录了一些访问过程中需要的元信息,依次是变长列的长度数组Variable Field Lengths,维护了所有变长列在当前Record的真实长度;Nullable Field Bitmap为允许Null的字段在当前Record是否为Null;一个1字节的Info Flags,截止8.0包括用作标记Record删除的Delete Mark Flag,用作标记是否是非叶子节点层最小Record的Min Rec Flag,以及标记是否为Instant Add Column之后加入的Instant Flag;Numbers of Records Owned用作下一节要介绍的B+Tree Page内数据维护,Heap No是该Record在其所在的Page上的序号,也是事务锁的加锁对象;Record Type标记Record的类型,包括叶子结点数据、非叶子节点指针等;最后是下一条Record偏移的Next指针,通过这个指针可以将Record串成链。
上面介绍的是记录完整的行数据的聚簇索引B+Tree中的Record格式,而对二级索引B+Tree中的Record格式略有区别,如下图所示,主要区别在于,其中的Key是建表是定义的二级索引列,其中的Value是对应的聚簇索引列,并且由于二级索引不维护MVCC信息,这里没有事务ID和RollPtr:
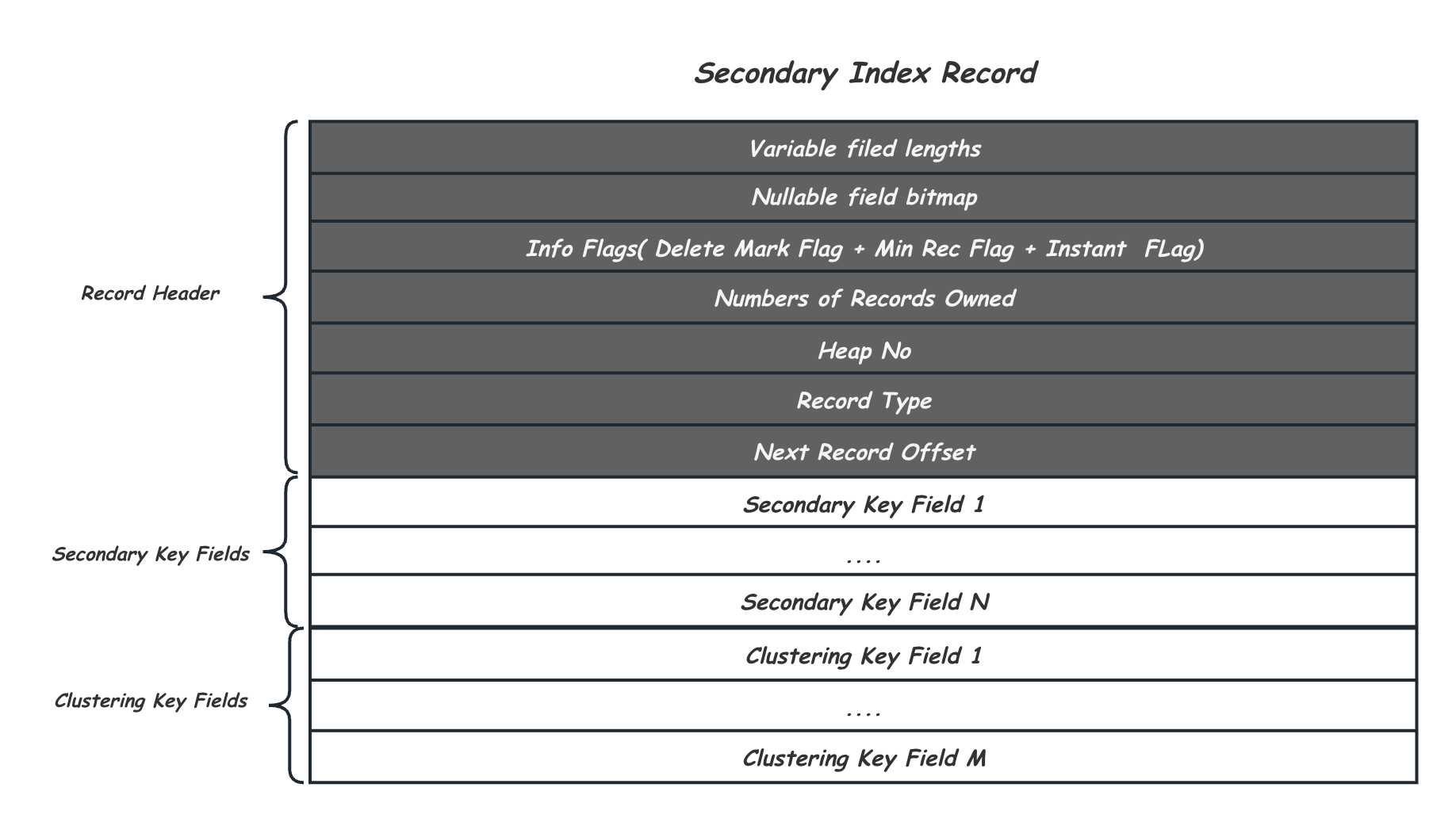
B+Tree中的节点:Page
InnoDB中B+Tree中的每一个节点,对应InnoDB中的一个默认16KB大小的Page,一个这样的Page中通常会维护很多的Record,这些Record通过上面介绍过的Record上的Next指针在Page内串成一个单向链表,除了真实的用户Record外,为了实现逻辑的简单,类似于我们通常处理链表问题时候采用的“哨兵”优化,InnoDB的B+Tree Page中也预留了两个固定位置固定值的System Records,在链表头的Infimum记录以及在链表尾的Supremum记录。由于B+Tree Page上维护的Records并不是定长的,无法通过Key方便的在页内做直接的定位,每次都做遍历查找的开又太大,因此InnoDB在Page内还维护了一个Record目录(Directory)来加速检索,这个Directory由多个连续存放的定长的Slot组成,每个Slot占用两字节,记录其指向的Record的页内偏移。综上一个B+Tree Page中的内容会如下图所示:
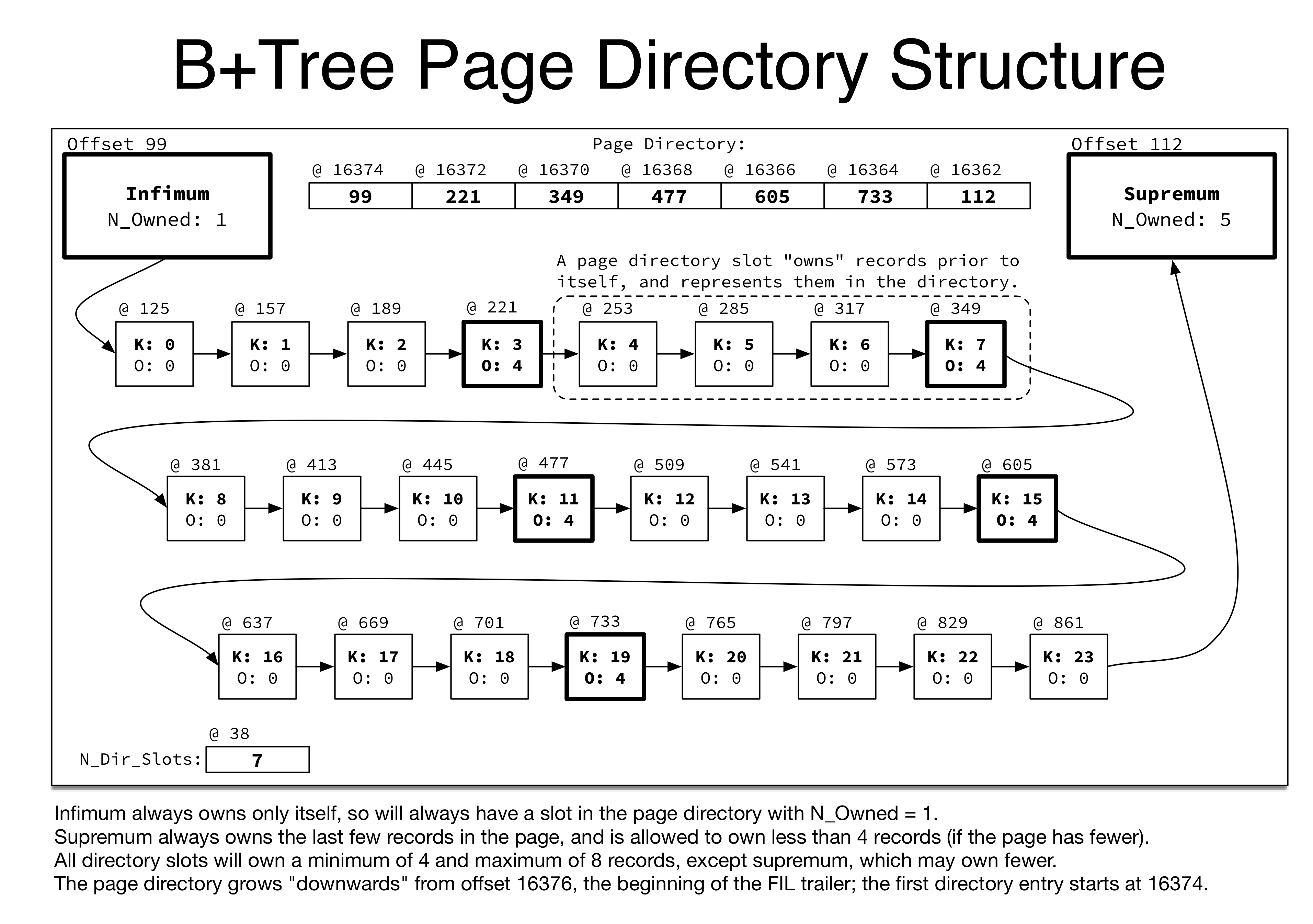
图中最上面所示的Page Directory中的每个Slot指向一个标粗的Record的页内偏移,开头和结束分别是Infimum记录和Supremum记录,两个这样的Record中间的Record称为被这个Slot Owned,一个Slot Owned的Record个数会记录在其指向的标粗的Record Header上的Numbers of Records Owned中。在插入和删除的过程中,这些Slot会动态的进行分裂或平衡,来保证除了最后一个Slot外,所有的slot所owned的Record在4到8之间。由于这些这些Directory slot本身是定长的,在做页内的Key查找的时候就可以很方便地通过这些连续的Slot数组来实现二分查找,找到其所Owned的这一组4到8个Records,再做顺序查找就大大提高了页内查询的效率。由于Page Directory中的Slot需要连续,并且随着Record的插入也需要不断的扩展,因此在实现上,不同于Record在页内自上而下的生长方式,Page Directory是从页尾向上的扩展的,二者中间的部分就是页上的空闲区域,如下图所示:
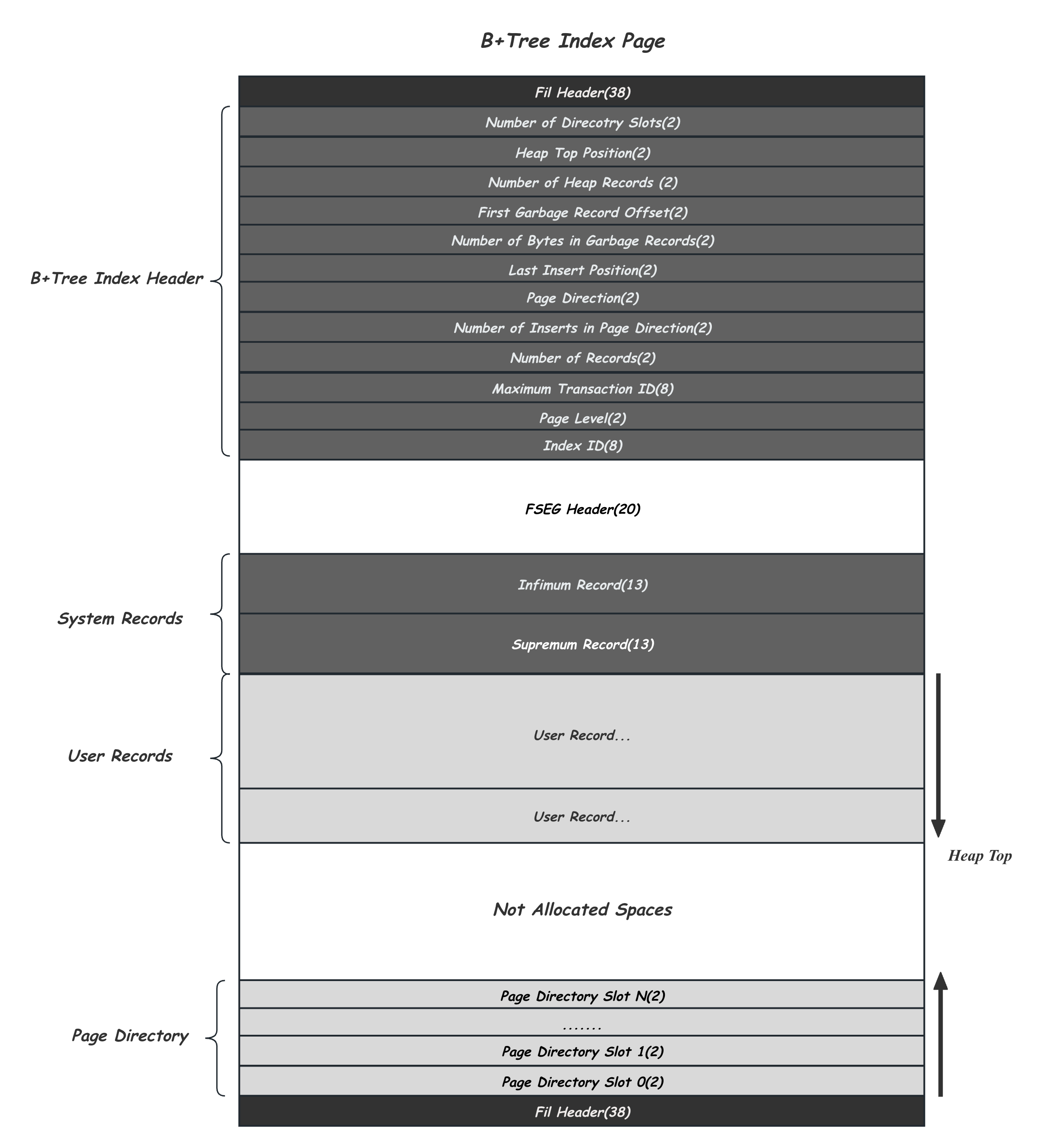
除了上面已经介绍过的System Record、User Record、Page Direcory以及他们之间的的未分配空间外,每个B+Tree的还会有一个定长的Index Header和一个定长的FSEG Header信息,其中FSEG Header只在B+Tree Root节点上有用,用户维护B+Tree的落盘结构,这部分我们放到最后一节的文件组织中介绍。这里我们主要关注Index Header,其中维护了很多元信息,依次为:Directory Slot的个数;User Record自上而下增长的位置Heap Top,这里是未分配空间的开头,新的记录都是从这里分配的;当前Page中曾经从Heap Top上分配出去的Record编号,每次新分配会加一,来作为这个Record位置的唯一标识记录在Record Header的Heap No中;除此之外,由于Record是可能删除的,Page还维护了一个简单的Free List,First Garage Record Offset就是这个链表头,紧接着的是这个Free List链表的元素个数,不过这个空闲链表得实现相当简单,当新的Record写入时,仅仅会尝试链表头的那个Record位置是不是够用,够就摘下来复用,不够就从Heap Top的位置上新分配;接下来的Last Insert Position维护的是上一次插入的的记录,为的是在页分裂的时候可以做一些启发式的规则,来避免顺序导入数据场景下,默认一半一半分裂的策略会造成的空间浪费;之后Page Direction是上一条记录插入的方向以及这个方向上连续插入的个数;当前Page的有效的记录数;修改当前Page的最大事务ID,这个值通常只在二级索引Page上有用,用作一些类似二级索引回表场景的过滤条件,以优化二级索引没有MVCC信息带来的回表开销;Page Levle是当前Page在B+Tree上的层级,叶子节点是0;最后是所属的Page所属的B+TreeIndex ID。
在开头的38个字节的Fil Header里除了当前Page的Checksum及Page LSN之外,还会有两个链表指针,在B+Tree中指向其兄弟节点的页编号,通过这个指针,每一层的Page都会组成一个横向的Page双向链表。同时,前面我们还讲过,B+Tree的非叶子节点中只会维护Key而没有Value,对非叶子节点来说,他的Value就是以这个Key为最小值的子节点页编号。最终一个B+Tree上的所有Page会通过纵向的子节点指针和横向的兄弟节点指针串成一个如下图所示的B+Tree:
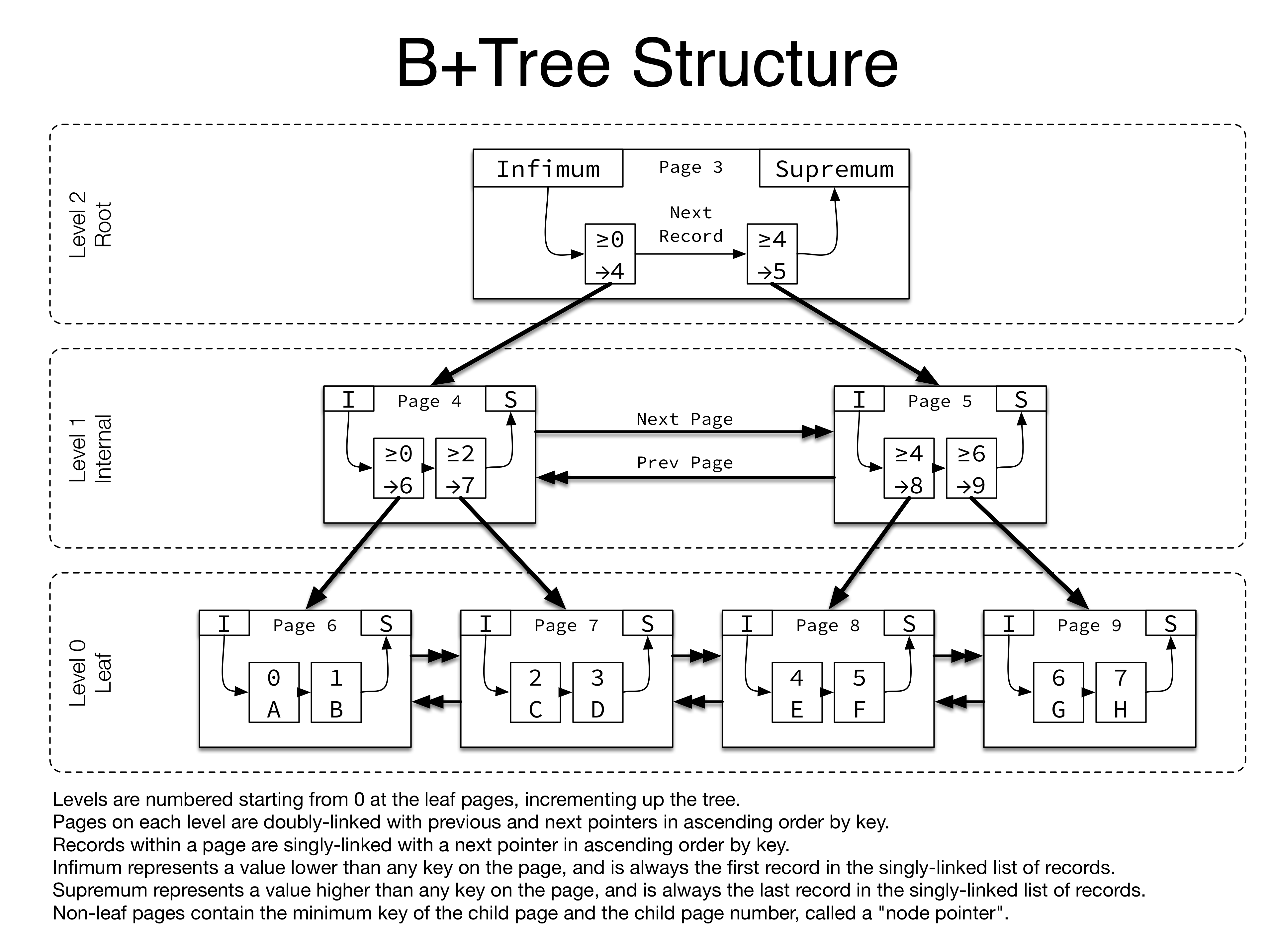
B+tree的访问
我们已经知道MySQL的所有的增删改查操作,经过Server层到InnoDB层,都会转换为一次次对表的聚簇索引或二级索引的B+Tree的查询、修改、插入及删除。这种从对行数据的操作到对B+Tree的操作的转换,并不总是一一对应的,主要包括如下三方面的因素:
- **行到Key Value的转换因素:**对行数据的修改操作,会造成行数据中某些或全部Field的变化,而这些Filed对于B+Tree来说,有些属于Key有些数据Value,当修改涉及到属于Key的Filed时,修改前后的行对于B+Tree来说其实是两条不同的记录,因此这次Update最终会变成B+Tree上老的Record的删除和新的Record的插入。
- **二级索引的实现因素:**上面在数据组织章节介绍过,InnoDB中的二级索引B+Tree的Value其实是其对应聚簇索引上的Key字段。从实现复杂度,尤其是对Lock的维护的复杂度上考虑,InnoDB不会对二级索引B+Tree上的Value做任何的修改,即使这个聚簇索引Key包含多个Field。如此一来,二级索引上的所有修改都会转换成B+Tree上对原来记录的删除和一次新记录的插入。
- **Ghost Record(Delete Mark)的因素:**InnoDB采用了《B+树数据库加锁历史》[4]一文中提到的Ghost Record实现,也就是删除操作只会对记录设置Delete Mark标记,而将真正的B+Tree上的记录删除推迟到后台Undo Purge中进行。而这个Delete Mark标记的引入,导致对Record的Delete和Insert操作可能会变成对Delete Mark标记的修改。
无论如何,这些操作最终还是会转换到B+Tree上的查询、修改、插入或删除,本章节还是站在B+Tree的角度上,来看看这一过程的实现,由于B+Tree上的Value都只存在在叶子节点上,因此所有的操作,第一步都需要先在B+Tree上完成对这个Key得定位。
B+Tree的定位
这个定位过程的逻辑主要在btr_cur_search_to_nth_level中,这个是个非常长且晦涩的函数,这里我们先忽略RTree、AHI、Insert Buffer、Blob以及下一章节将要介绍的并发控制相关内容后,其逻辑其实是非常简单的:首先,这个函数的调用者会指定要查找的Key Field值以及Search_Mode(大于、大于等于、小于、小于等于);然后从描述这个B+Tree的数据字典元信息dict_index_t中,获得这个B+Tree的Root Page Number,通过buf_page_get_gen去获取这个这个Page,如果不在Buffer Pool会先从磁盘中加载进内存;之后,通过page_cur_search_with_match去做页内的搜索,包括根据Directory Slot的二分查找,以及定位到对应Slot后对其Owned Records的顺序遍历,找到需要的Key范围,得到下一层的Page Number,重复上面的这个buf_page_get_gen + page_cur_search_with_match过程,直到找到满足Search_mode的叶子节点上的Record位置。这个位置信息会维护在一个btr_cur_t结构中,供调用者使用,也可能固化在当前线程的btr_pcur_t结构中,btr_pcur_t中的除了包括位置信息外,还包括一个获得这个cursor时候的版本号,通过这个版本号,后续的访问只要发现这个Page没有改动就可以直接使用这个位置信息,避免重复的B+Tree定位过程。后续的操作都会基于这个位置信息Cursor做操作,其中读取是最简单的,直接获取Value信息即可。
B+Tree的修改、插入、删除
InnoDB中对B+Tree的修改、插入以及删除操作都会存在乐观和悲观两个版本,乐观版本假设本次操作不会导致树结构的变化,因此持有较轻量的锁,如果失败,那么就获取更重的锁,再通过悲观版本来完成变更。这里得修改包括对非Key Filed的修改,也包括对Delete Mark的修改,一次Update的过程如下:
- btr_cur_optimistic_update会比较要修改的Record的老值和新值占用的空间大小,如果新值更小,那么简单的通过btr_update_in_place在当前位置直接更新,并接受Record变小带来的碎片。
- 如果新值需要的空间更大,那么就需要先在Page上删除老的Record,再插入新的Record,这时会先计算删除后是否有空间插入新的的Record,如果能,那么通过page_cur_delete_rec删除,之后再通过btr_cur_insert_if_poossible再次插入就好。
- 但如果Page上无法放下新值,那么就需要返回失败,并在加更重的锁之后通过btr_cur_pessimistic_update来完成,这里先page_cur_delete_rec完成删除,然后通过btr_cur_pessimistic_insert来做悲观插入,其中可能需要先完成B+Tree的节点分裂甚至是树层数的增高。
需要指出的是这里的删除和插入的Record的Key是完全一致的,对B+Tree来说他们还是同一条记录,只是由于空间变化问题换了个位置,新的Record会继承老Record的MVCC需要的Undo版本链,以及可能存在的记录锁。这个过程中触发的Page内的Record插入或者删除,都会维护上面所讲到的页内Record链表,Free List以及Directory Slot,如下图所示,是一次将Record修改成占用空间更大的值的过程,由于原来的Record空间不足以存放新值,因此需要先将老的Record空间删除,之后再插入一个新的存放了新值的Record,同时老的Record被加入到了Free List(Garbage)中。
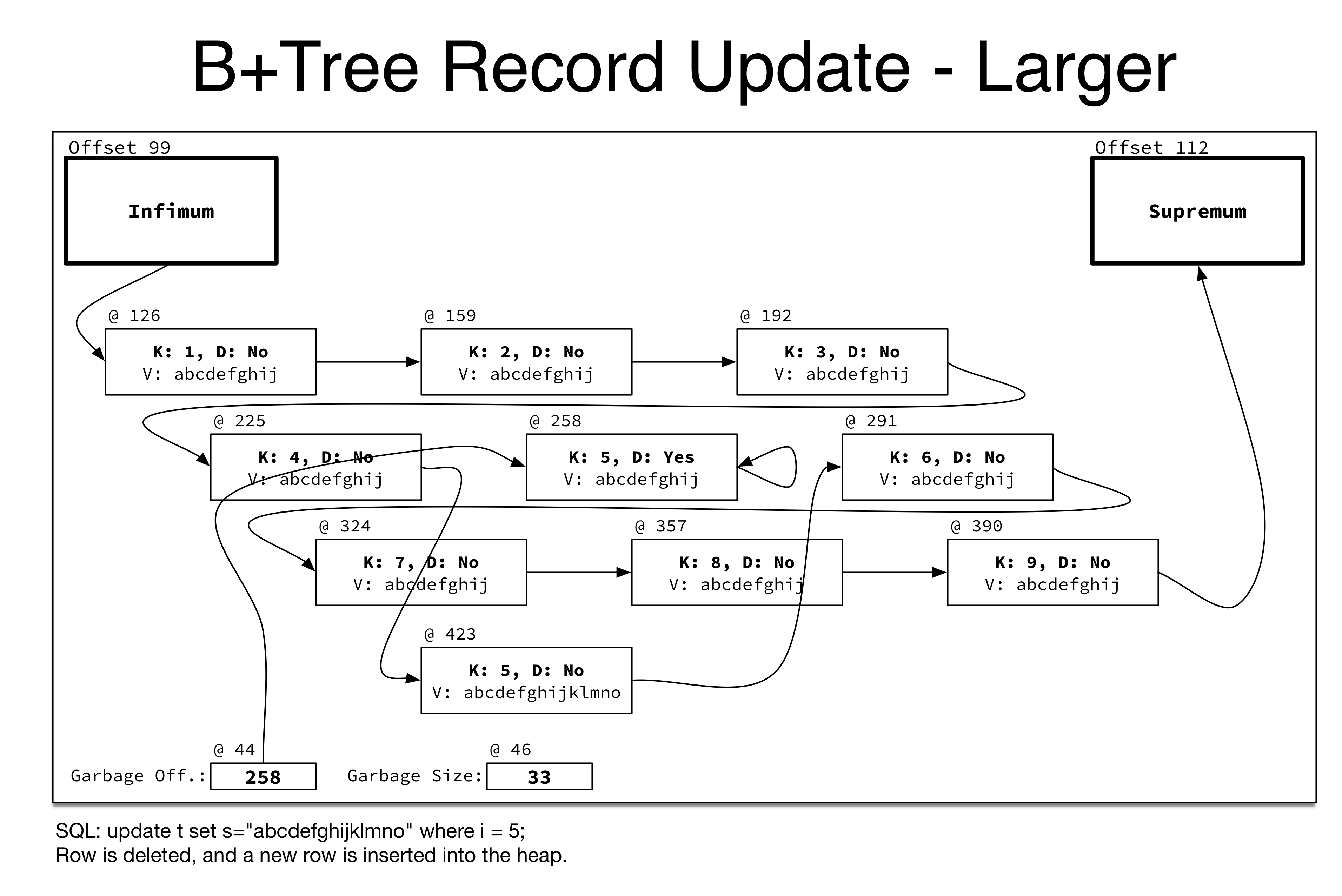
对于插入操作而言,同样先乐观的通过btr_cur_optimistic_insert尝试插入,如果Page内空间充足,那么通过page_cur_tuple_insert完成页内插入,否则返回失败,之后通过btr_cur_pessimistic_insert来做悲观插入,悲观插入会带来节点的分裂,甚至树层数的升高。类似的,删除操作会先乐观地通过btr_cur_optimistic_delete来删除,其中需要先采用btr_cur_can_delete_without_compress判断删除后是否需要触发Page合并,也就是Page中的剩余Record值是否小于了阈值。如果不会,那么通过page_cur_delete_rec完成删除。否则,需要返回失败,并在之后通过btr_cur_pessimistic_delete做悲观的删除,也就是在删除后触发Page的合并,甚至是树层数的降低。
B+Tree的节点分裂及树高度上升
当前Page的空间无法放下要插入的Record的时候,就需要触发当前Page的分裂,由于B+Tree的所有Value都只存在于叶子结点,因此,通常情况下节点的分裂都是从叶子节点的分裂发起的,叶子节点分裂后,新的节点插入到父节点中,导致级联的上层Page分裂。除此之外还有一种情况,就是下层节点删除第一项,会导致当前节点的边界Key发生变化,那么就需要在其父节点中删除对应老的Key,并插入新的Key,这个插入动作也是有可能导致父节点的分裂的。
节点分裂的实现代码主要在btr_page_split_and_insert中,第一步是要(1)确定split_rec,也就是从那个位置开始把之后的Record移动到新分裂出来的Page上去,一般情况下,这个split_rec会选择当前Page中间的那个,也就是分裂后的两个兄弟节点每人负责一半的数据。但这样一来,在主键Autoinc导入数据这样的场景中,插入的数据是有序递增的,那么前面的一个Page就永远只有一半的数据,整个B+Tree的空间利用率就变成了50%。为了尽量避免这种情况,InnoDB中采用了简单的启发式规则,这就要用到前面我们再Page格式中介绍的,Index Page Header上的信息:Last Insert Position,基本思路是如果这个Page上的两次连续的Insert是刚好有序的两个Record,那么很有可能当前是一个顺序插入的场景,那么就不要选择中间位置分裂,而是直接从这个插入的位置来做分裂。
确定了split_rec之后,接下来的分裂操作就比较简单了,首先(2)从文件上分配并初始化一个新的Page,并通过btr_attach_half_pages将这个新Page加入的B+Tree中,包括向父节点中添加这个新节点的Key及指针,以及将这个Page加入同一层的兄弟节点的双向链表中,注意向父节点的插入操作可能触发级联向上的Page分裂;之后(3)将前面找到的split_rec后面的Records拷贝到新的Page上去,并在老的Page中删除;(4)最后再完成新Record的插入即可,这个插入有可能插入新节点也有可能插入老节点,取决于前面split_rec的选择。这里实现上有一个小细节,在选取spilit_rec的时候第一次直接选中间节点可能会导致分裂后还是放不下,那么会触发第二次分裂,而这一次会参考要插入的rec大小和Page内当前的Record大小,来选择一个分裂后一定能放下的split_rec,也就是btr_page_split_and_insert中一个节点的分裂是有可能分裂成三个节点的。整个分裂过程如下图所示:
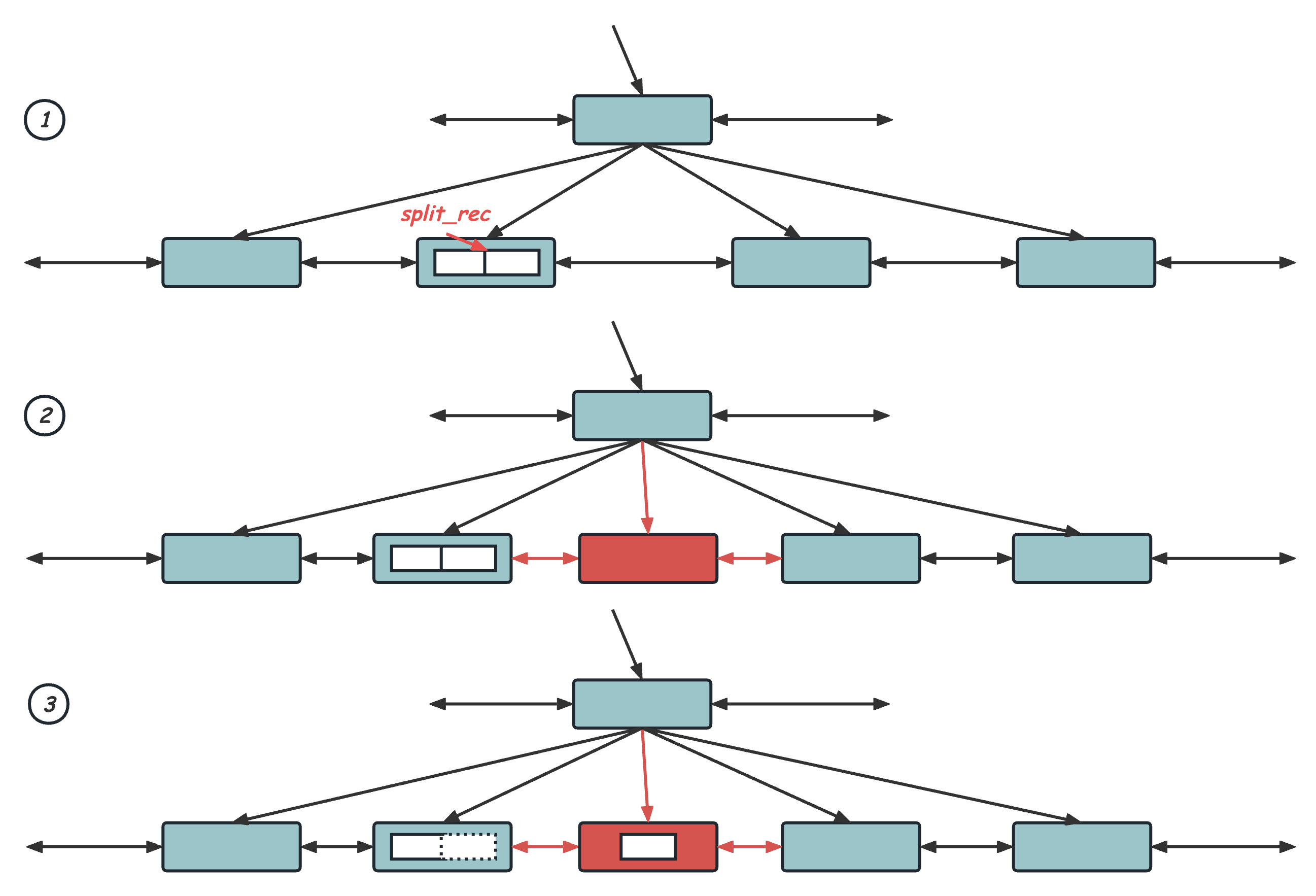
在整个B+Tree都很满的情况下,这种从叶子节点发起,一路向上的级联节点分裂,有可能一路传到到Root Page,造成Root Page的分裂,而Root Page分裂会带来整个B+Tree层数的变高。这个过程的实现主要咋btr_root_raise_and_insert中,由于Root Page头中有一些特殊的信息,并且这个位置是记录在数据字典中的,我们不希望Root Page的分裂带来这些信息的修改,因此这里采取了保留原Root的Page的方式:首先分配一个新的Page,将Root上的所有记录都拷贝到这个New Page上,然后清空Root Page并将这个New Page挂到Root Page上作为其当前唯一的叶子节点,之后同样调用btr_page_split_and_insert来完成一次常规的Page分裂过程。
B+Tree的节点合并及树高度降低
从Page上删除Record的时候,如果造成Page上的空间占用低于一个阈值merge_threshold,那么就会触发节点合并,这个阈值默认是50%,当然也可以对整个Table或者单个索引通过设置COMMENT='MERGE_THRESHOLD=40’来修改为1到50中间的任何一个数。大多数的节点合并都由叶子节点上删除数据触发叶子结点的合并开始,如果需要删除父节点中的元素,就可能触发级联的上层节点合并。但有一种例外,是在做节点的插入操作时,如果当前节点无法放下并且是最后一个Record,那么就会首先尝试btr_insert_into_right_sibling插入到右边的兄弟节点,这个新的插入就会是右侧兄弟节点的第一个Key,而修改第一个Key就需要先从父节点中删除原先对应这个节点的Key,然后插入新的,这个删除操作同样有可能会触发父亲节点进而级联向上的节点合并。
节点合并的操作通常主要在btr_compress中完成,其中首先会通过btr_can_merge_with_page依次判断其左右兄弟节点是否足以放下要合并节点的所有记录,如果可以放下就进入正式的合并过程:将当前Page中的所有记录拷贝到要合并的兄弟节点中去,将这个节点从兄弟节点的双向链表中移除,并更新或删除父节点中的对应Key或指针,这个过程可能会触发级联向上的Page合并。
但如果当前要合并的节点已经没有左右兄弟节点,也就是说这个节点是B+Tree上当前Level的最后一个Page,那么就需要将当前节点与其父节点进行合并,也就是将当前的节点上升一层,这个过程在btr_lift_page_up中,首先将这个父节点清空,然后将原来节点的所有内容拷贝到其父节点中,之后将这个原来的节点Free掉即可,从而也导致整个B+Tree高度的降低。








