我们日常生活中常用的数字通常是实数,比如整数、小数、分数等。实数的集合用字母 R 表示。
一个方程的解可能在实数范围内无解。比如说,方程
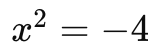
任何实数的平方都不可能是负数。但是如果我们引入虚数单位 i ,
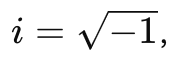
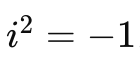
那么上述方程的解就变成了
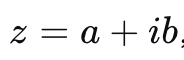

复数不仅解决了上述方程解的问题,实际上,数学家们证明了所有一元及以上的多项式方程都能在复数范围内找到解。这就是著名的代数基本定理。
复数 z 的复共轭,表示为 z*,定义为
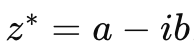
如果复数 z = a + ib 和其共轭 z* = a - ib 相等,那么 z 就是实数。 如果 z* = -z z 就是纯虚数。 0 既是实数也是虚数。
复数的模,记作 |z|,是复数的“大小”,它的计算公式是:
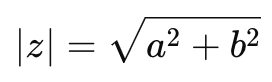
很容易验证,
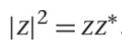
复数在二维复平面中表示为矢量
实部 a 虚部 b 对应平面中的 y 轴。
因此,复数
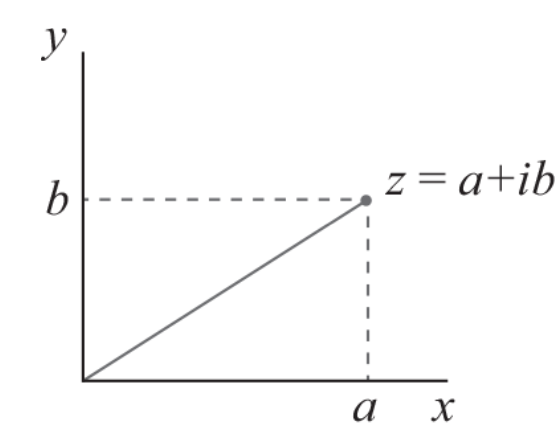
复数的模 |z| 就是这个向量的长度。
欧拉公式是复数的一个非常重要的公式,它将指数函数与三角函数联系起来,公式为:
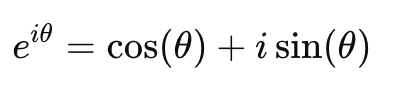
这个公式告诉我们,复数
复数不仅可以在直角坐标系中表示,还可以在极坐标系中表示。在极坐标中,复数可以表示为:
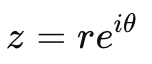
其中:
r = ∣ z ∣ 是复数的模,表示复数的“大小”; θ = arg ( z ) 是复数的 辐角,表示复数与x 轴的夹角。
事实上,物理学中的所有测量结果都是实数。然而,在量子力学中,复数是基本的。薛定谔方程左侧包含虚数单位 i,这使得方程的解不可能是实数解,只能是复数。事实上,波函数Ψ本身就是一个复值函数。这意味着,它在每个空间点和时间点都有一个复数值。
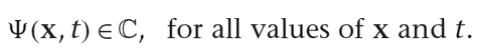
量子力学中的波函数解与经典波动方程的解不同,经典波动方程涉及二阶时间导数,而薛定谔方程只涉及一阶时间导数。这个一阶导数与 i 的乘积是允许波动存在的关键因素。
由于复数不能直接测量,波函数和可测量之间必须有些间接联系。玻恩的建议是将波函数的模平方与概率(始终是非负实数)等同起来。因此,给定一个量子系统的波函数 Ψ,对于某一事件的概率是:

因此,波函数 Ψ 通常被称为概率幅。量子力学提供了一种令人惊讶的概率计算方法。理论中的薛定谔方程本身是关于概率振幅(波函数 Ψ)的方程,而不是关于实际概率的方程。我们通过计算波函数的模平方来获得真实的概率。
表达量子力学定律所需的数学框架由复向量空间组成。在任何向量空间中,我们都有可以相加的对象,并称之为向量。在复向量空间中,一个向量乘以复数仍然是一个有效的向量。在量子力学中,波函数 Ψ 被认为是复数向量空间中的一个向量。复数向量空间提供了处理量子态和量子力学算符强有力的工具。






