


点击上方 蓝字关注我们
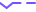
题目:On Provable Benefits of Depth in Training Graph Convolutional Networks
作者:
Weilin Cong (Pennsylvania State University)
Morteza Ramezani (Pennsylvania State University)
Mehrdad Mahdavi (TTI Chicago)

主要内容
我们知道随着图网络层数的增加,图卷积网络(GCNs)的性能会显著下降,这通常归因于过平滑(oversmoothing)。尽管有明显的共识,但本文作者观察到,在理论上对过平滑的理解与GCNs的实际能力之间存在着差异。具体地说,本文作者认为过平滑在实践中并不是必然发生的,可以证明, 更深层次的模型以线性收敛速度收敛到全局最优。只要训练得当,就可以达到很高的训练精度。
小编:但是为什么深层的图神经网络的效果差呢?看看本文作者的研究。
尽管能够达到较高的训练精度,但实证结果表明,更深层次的模型在测试阶段的泛化能力较差。为了更好地理解GCNs,本文作者仔细分析了GCNs的泛化能力,分析表明,是训练的方式显著降低了GCNs的泛化能力。在这些发现的启发下,作者提出了一种GCNs的解耦结构,将加权矩阵从特征传播中分离出来,以保持表达能力并确保良好的泛化性能。为了验证提出的理论的正确性,作者在各种模拟数据集和真实数据集上进行了实证评估。

Introduction
近年来,图卷积网络(GCNs)在处理图结构的应用方面取得了最先进的性能,但在大型稀疏图上使用浅层GCN并不是十分有效的[22,6,19,8,45]。因此,需要一个更深层次的GCN模型来获取和聚合来自更远邻居的信息。尽管与传统的深层神经网络不同,较深的GCN更倾向于感知更多的图结构信息,但较深的GCN潜在地受到过平滑[34,40,25,4,57]、梯度消失/爆炸[32]、过度over-squashing的影响。最被广泛接受的原因是“过平滑”,这是由于应用多个图卷积使得所有节点embedding收敛到单个子空间(或向量)而导致节点表示不可区分的现象,传统的观点认为增加层数会导致过度平滑,从而削弱GCNs的表达能力,从而导致训练精度较差。
作者注意到:根据过平滑的定义,即随着GCNs的深入,节点表示变得无法区分,分类器很难为每个节点分配正确的标签,训练精度会随着层数的增加而降低。然而,如图1所示,
图1中的结果可以通过删除丢弃和重量衰减操作来复现。这两个改进旨在提高模型的泛化能力(即验证/测试精度),但由于训练过程中引入的模型参数的随机性和额外的正则化项,可能会损害训练精度。可以找到使用DGL的简单实验
https://github.com/CongWeilin/DGCN/blob/master/DGL_code.ipynb
无论层数多少,GCN都能够实现高训练精度。同时,也可以观察到,较深的GCNs需要更多的训练迭代才能达到较高的训练精度,并且其在测试集上的泛化性能随着层数的增加而降低。这一观察表明,性能下降可能是由于不适当的训练,而不是过度平滑导致的低表现力。否则,一个表达能力较低的模型仅靠适当的训练技巧不能达到近乎完美的训练精度。
基于上述观察,本文旨在回答两个基本问题:
Q1:增加深度真的会削弱GCN的表达能力吗?
在第四节中,本文作者论证了基于过平滑的理论结果与深层GCN模型的实际能力之间存在差异,说明过平滑并不是导致更深层次GCN性能下降的关键因素。。特别地,本文作者从数学上证明了over-smoothing[40,25,34,4]主要是理论分析的产物和分析中的简化。实际上,通过刻画GCN的表示能力,Weisfeiler-Lehman(WL)图同构检验[38,54]表明,深层GCN模型的表达能力与浅层GCN模型一样少,只要GCN训练得当,深层GCN模型可以区分出浅层GCN无法区分的不同邻域的节点。此外,本文作者从理论上证明,对于较深层的模型来说,较多的训练迭代,可以以达到与浅层模型相同的训练误差,这进一步表明,深层GCN训练中较差的训练误差很可能是由于不适当的训练造成的。
Q2:如果有表现力,那么为什么深层GCN泛化得很差
在实验方面,本文作者对GCNs及其变体(如ResGCN、APPNP和GCNII)在节点分类任务的半监督设置下进行了一种新的泛化分析。发现GCNs的泛化差距与训练迭代次数、最大结点度、权重矩阵的最大奇异值和层数有关。特别是,本文作者的结果表明,更深的GCN模型需要更多的训练和优化迭代才能收敛(例如,添加跳过连接),这导致了较差的泛化。更有趣的是,泛化分析表明,大多数所谓的解决过光滑问题的方法[46,60,6,28]都能极大地提高模型的泛化能力,从而得到更深层次的结果.
在第六节中,本文作者提出了一种新的框架--解耦GCN(DGCN),该框架能够训练更深层次的GCN,并能显著提高泛化性能。其主要思想是通过将权重参数与特征传播解耦来分离表达能力和泛化能力。

相关文献-关于GCN的泛化性能
近年来,许多文献使用一致稳定性[49,62]、神经切核[14]、VC维[48]、Rademacher复杂度[17,41]、算法对齐[55,56]和PAC-Bayes[35]来推广广义神经网络。现有的研究只关注一个具体的GCN结构,不能用来理解GCN结构对其泛化能力的影响。与我们关系最密切的是[49],他们在文[49]中分析了单层GCN模型的稳定性,并证明GCN的稳定性取决于其拉普拉斯矩阵的最大绝对特征值。然而,他们的结果是在归纳学习环境下得到的,并且将结果推广到不同结构的多层GCNs是 non-trivial.

观察分析
[34] Deeper Insights into Graph Convolutional Networks for Semi-Supervised Learning
过平滑是指在将多个图形卷积运算应用于节点特征之后,所有节点嵌入都收敛到单个向量的现象。然而,文献[34]只考虑了无非线性的图形卷积运算和每层权重矩阵。为了验证正常GCNS中是否存在过平滑,我们测量了随模型深度变化的归一化节点嵌入之间的成对距离。如图2所示,(左图)在没有权重矩阵和非线性激活函数的情况下,节点嵌入之间的成对距离确实随着层数的增加而减小。
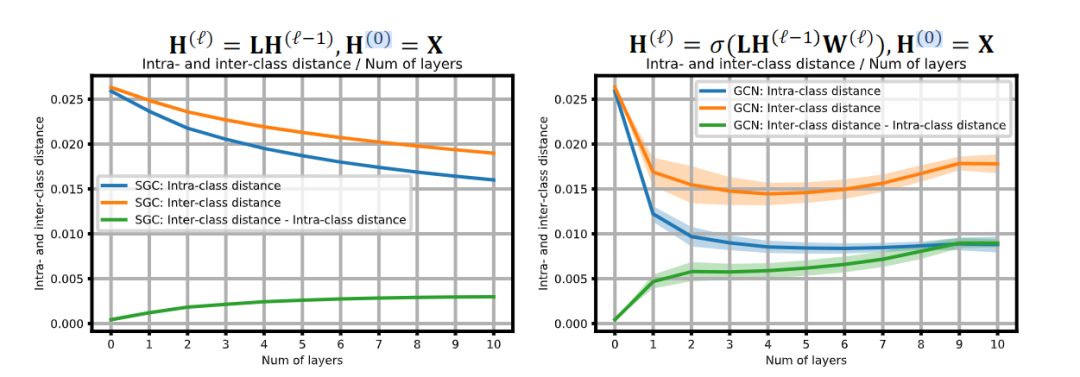
然而,(右图)考虑到权重矩阵和非线性,两两距离实际上是在一定深度之后是增加的,这与过平滑的定义相矛盾,非线性和权重矩阵帮助节点嵌入在卷积后保持可区分性。
[40] Graph Neural Networks Exponentially Lose Expressive Power for Node Classification
[25] Two Sides of the Same Coin: Heterophily and Oversmoothing in Graph Convolutional Neural Networks
最近,[40,25]通过同时考虑非线性和权重矩阵,推广了过平滑的概念。更具体地说,他们使用定义为节点嵌入到仅具有节点度信息的子空间M的节点嵌入距离d_M来测量第l层节点嵌入H^l的表现力。设λ_L是图的拉普拉斯矩阵的第二大特征值,λ_W是权矩阵的最大奇异值。[40][25]表明d_M(H)是受到(λ_W*λ_L)^l*d_M(x)约束的,也就是节点嵌入的表现力将随着层数的增加而指数降低或增加,其中增加还是较少是受到λ_W*λ_L与1的关系决定。[40][25]作者认为λ_W*λ_L<1,所以深度GNN的表现力是指数级递减的。而本文作者argue这种假设是不成立的。本文作者提出来:
W矩阵一般按照uniform distribution N(0, sqrt(1/d_l-1))来进行的,根据之前的工作,他的最大奇异值λ_W上界是:1+某个值,它是大于1的。另外lambda_L一般也是接近于1的,比如cora,citesser,pubmed的lambda值分别是0.9964, 0.9987, 0.9905,所以本文作者认为[40][25]说的λ_W*λ_L<1不正确。同时作者也进行了实验发现d_M在没有训练过的GNN上,最层数指数级衰减,但是在训练过的GNN上却不一样。

作者认为GCN层数越深,表达能力越强,那么怎么刻画表达力(expressiveness)呢?

我们后面继续看看(未完待续)







