KDD2021 || HTGN: 双曲空间下的时态/动态图嵌入
「作者」:Menglin Yang, Min Zhou, Marcus Kalander, Zengfeng Huang, Irwin King
「论文」:Discrete-time Temporal Network Embedding via Implicit Hierarchical Learning in Hyperbolic Space
「链接」:https://arxiv.org/abs/2107.03767「Code」: https://github.com/marlin-codes/HTGN
「导读」: 动态网络模型在静态网络的基础上增加了时间维度,使其能同时表征复杂系统的结构和时序信息,在生物、医药、社交网络、电信网络等领域有广泛的应用场景。目前的动态图模型主要集中在利用欧式空间来学习网络在时间和空间上的演变规律。然而,层级结构广泛存在于网络数据中,在欧式空间对具有层级特点的网络进行表征学习会引起较大的嵌入失真从而大大影响下游任务的效果。双曲空间可以看作是‘连续型的树状结构’空间,在描述数据层级结构的时候具有天然优势。另一方面,双曲空间具有更大的容纳体积,即利用较少的嵌入维度即可实现较好的表征效果,从而可以较大幅度减少模型参数。基于此, 作者将双曲几何运用到动态网络建模中,提出了一种基于双曲空间的动态图表征模型HTGN (hyperbolic temporal graph network)。HTGN将动态图映射到双曲空间中,并进利用双曲图神经网络和双曲门控递归神经网络学习数据中的时空依赖性。此外,根据动态网络演变特性,进一步设计了HTA(hyperbolic temporal attention)和HTC(hyperbolic temporal consistency)两个模块,使得HTGN能有效的在双曲空间进行网络演变的学习。最后,作者在多个公开数据集上的实验结果验证了HTGN在动态图嵌入问题的有效性。与最优的基线模型相比, HTGN在不同类型的动态链路预测任务上都有非常显著的效果提升。此外,消融实验也进一步验证了双曲几何的表达能力以及HTA和HTC模块的有效性。
1. 双曲图神经网络
双曲空间在建模具有层级结构或Power-law分布的数据上有天然的优势。这个优势主要来自它的metric和距离公式。这里我们不对公式进行过多介绍,下面给一个直观的例子。(与欧式空间不同的是,双曲空间有多个模型可以刻画,下面以Poincare Ball为例子简单介绍一下).

如上图所示,Poincare Ball model是通过将嵌入空间限制在单位球内的一种双曲模型。在庞加莱球的双曲模型中,上面所有明暗相间的三角形都是相同大小的,而在我们欧式的角度去看,靠近边缘区域的三角形相对较小。换一种理解的方式,如果以欧式的角度看,把上面圆的中心当作原点,随着半径的增加,三角形的个数是越来越多的。而这个增长的速度是指数级的,这与具有树形结构的数据(或者scale-free network)能够很好地匹配. 而在真实世界中的网络中很多具有这样的特点,比如微博中用户的被关注量,推荐系统中商品的销售量,网络主播的被关注量,所交的税收,居民的收入等等。本文研究随着时间变化的网络结构。
2. 时序网络数据建模的离散化
对于时序图数据的预处理,目前主要有两种方法:离散的快照(discrete snapshots) 以及连续的方法(countinuous method).两种方法都有各自的优点和不足,本文采用的是离散的快照。
离散的快照是一种简单的处理的方式,它主要把时序的网络数据按照一定的时间间隔切成一系列的快照,每一个快照可以认为是一个静态的图网络结构。基于此,目前的研究方时序图网络的方法主要从两个方面考虑:当前时刻的联系/交互等形成的拓扑依赖或者结构关系;另一方面,对演化规律的建模,捕捉数据的动态变化趋势。
建模当前时刻的拓扑可以通过图神经网络比如图卷积神经网络(GCN)和图注意力神经网路(GAT); 捕捉数据的动态变化趋势可以通过循环神经网络进行学习,如RNN, GRU, LSTM等。
3. Motivation
建立时间变化的图网络,目前大多数的模型都是建立在欧式空间中,这不难理解。欧式空间有非常多的优势,比如(1)欧几里得空间非常符合我们直觉,(2)欧式空间也能够很好地进行可视化,(3)欧式运算具有成熟的矢量空间,以及(4)定义好的距离/内积的公式。然而,嵌入质量的好坏取决于嵌入空间的几何形状与数据结构的匹配程度。这引发了一个基本问题:广泛使用的欧几里得空间是否是时态图网络络嵌入的最佳选择。目前有很多的图是服从power-law分布的,比如论文中提到的社交网络和引文网络。
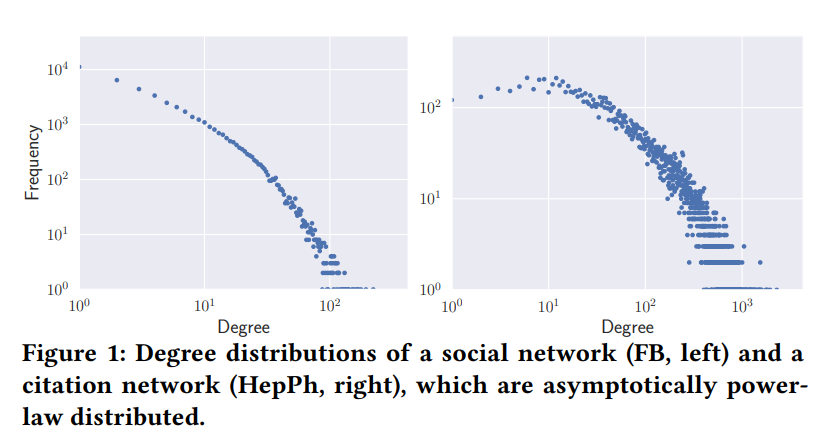
最近,双曲几何受到越来越多的关注,并在很多静态图嵌入任务中实现了先进的性能。双曲空间的一个基本特性是它的容量呈指数级扩展,可以看作是树的连续版本,能够很好地嵌入具有指数级增长的数据。因此,具有层次结构和树状的数据自然而然地可以使用双曲几何表示。但是反过来,如果将这些图直接嵌入欧几里得空间,则会导致严重的结构归纳偏差和高失真。
基于此,本文作者考虑将第二部分中提到的两个基本模块泛化到双曲空间,从而充分利用双曲空间的几何特性和结构特点。
3. HTGN模型
本文的模型HTGN非常简单,遵循GNN-GRU的建模思路。HTGN模型包含了三个模块,双曲图神经网络,双曲循环神经网络,计算历史状态的注意力模块。下面分别进行介绍。
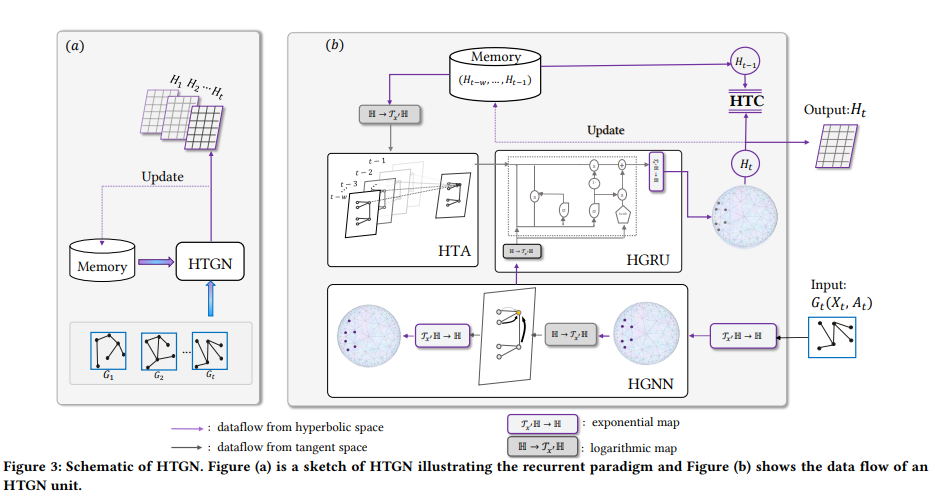
(1) 双曲图神经网络(HGNN)
双曲图神经网络是用来提取模型的拓扑结构,也就是对当前的快照进行建模。HGNN利用双曲几何来学习图中的拓扑依赖关系。与GNN类似,HGNN 层也包括三个关键操作:双曲变换、双曲聚合和激活函数。
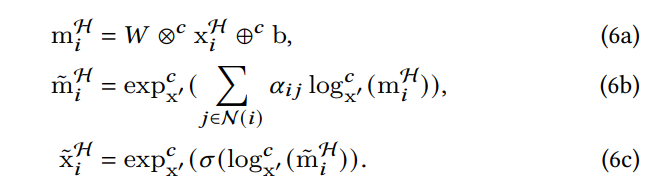
其中6a, 6b, 6c分别是双曲变换、双曲聚合和激活函数。
(2) 计算历史状态的注意力模块(HTA)
在第一步中,提取了当前网络的状态,但是这往往是不够的,历史状态对于网络的预测也非常的重要,那么提取多少时刻的历史状态呢?这里作者提出了一个HTA模块,简单的来说对过去的w历史时刻计算一个注意力,进行加权。
算法如下面所示

这里面包含了两个注意力,一个是时间维度的(r),一个是空间维度的(Q)。
(3) 双曲循环神经网络
接下来的就是双曲循环神经网络,这里作者将其映射到切空间上进行
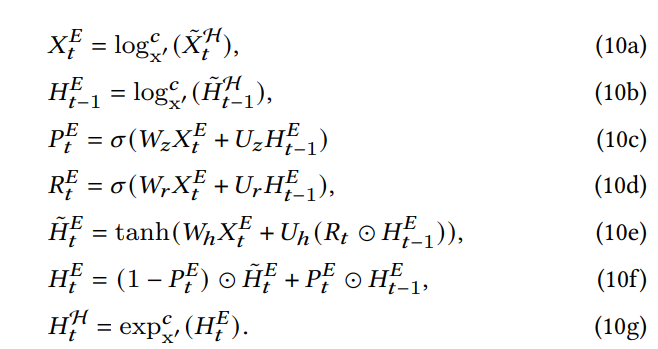
当然也可以采用HyperGRU的方式(defined by Ganea et al),但是计算代价太大。
(4)双曲空间下时序数据的连续性假设
本文作者考虑两个loss function, 第一个是图上的Homophily Loss,这个loss假设有交互/连接的节点通常属于同一类或具有相似的性质。对应的损失函数如下
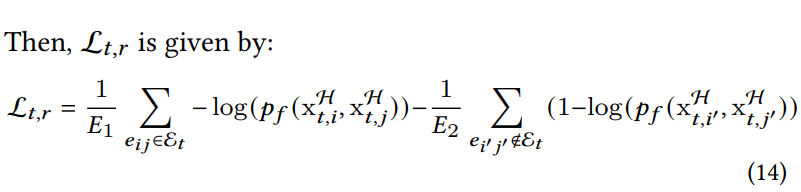
其中衡量了(i,j)两个节点在双曲空间连接的概率,上面公式表示的含义是最大化有交互过或者有连接节点对的概率,最小化没有交互过或者没有连接节点的概率
第二个是时间序列中的consistency loss,这个loss假设节点的变化在嵌入空间的位置变化是平滑和连续的,对应的损失函数如下
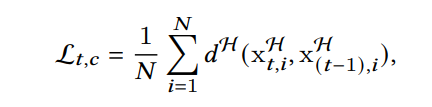
其中表示节点i前后两个时刻的嵌入距离,这个公式的含义是约束节点的变化是连续的。
4. 实验部分
本文作者对比了多种模型和数据,提升显著。
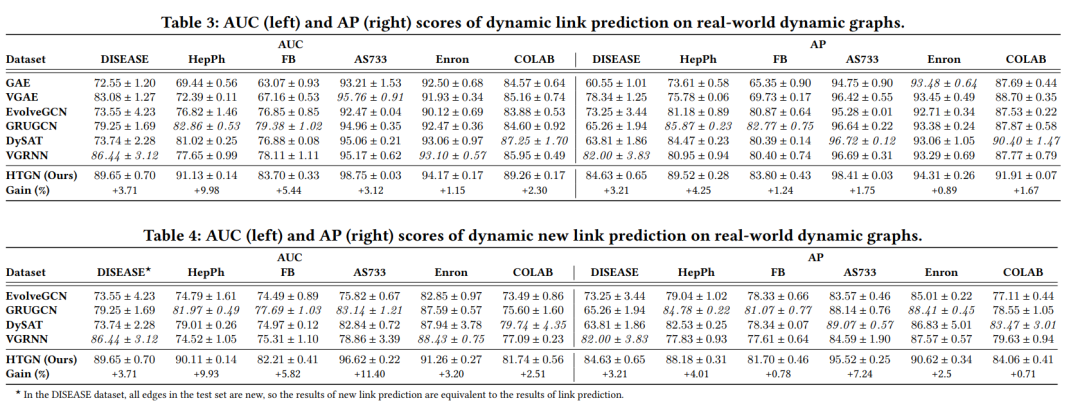
除此之外,作者对各个模块以及双曲几何进行了,消融实验
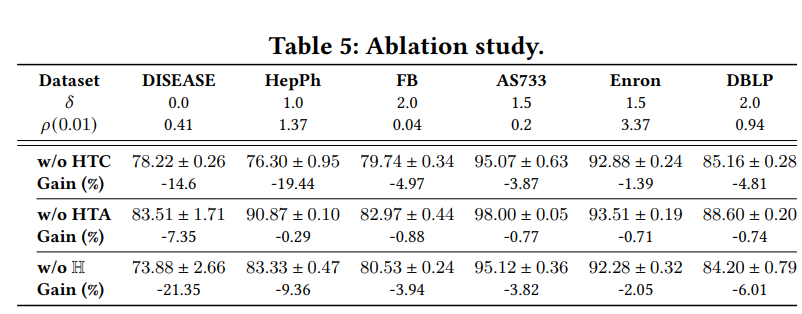
整体回顾
在这项工作中,作者介绍了一种新的基于双曲几何的节点表示学习框架,称为双曲时间图网络 HTGN,用于时间图建模。总体而言,HTGN 遵循简洁有效的 GRNN 框架,利用双曲图神经网络的作用学习数据中潜在的分布。更具体地说,本文提出了两个模块:双曲时间上下文注意离模块(HTA)和双曲时间一致性(HTC),分别提取注意力的历史状态并确保稳定性和泛化性,以推动HTGN的成功。







