ICML 2022 | Optimization-Induced Graph Implicit Nonlinear Diffusion
“文章信息
来源：Proceedings of the 39th International Conference on Machine Learning（ICML） 2022
”
标题：Optimization-Induced Graph Implicit Nonlinear Diffusion
作者：Qi Chen, Yifei Wang, Yisen Wang, Jiansheng Yang, Zhouchen Lin
链接：https://proceedings.mlr.press/v162/chen22z.html
内容简介
近年来，图神经网络（GNNs）成为了先进的图挖掘模型。尽管 GNN 的应用取得了巨大成功，然而这些 GNN 通常缺乏捕获远程依赖关系的能力。特别是在常见的消息传递中，GNN 只能通过 个传播步骤聚合来自 跳邻居的信息。现有的研究工作已经观察到，当传播步骤 (Li et al., 2018) 时，GNN 通常会发生灾难性的退化，这种现象被广泛描述为过度平滑。一些研究试图通过更具表现力的高阶邻居聚合来缓解它，然而，它们捕获全局信息的能力本质上仍会受到有限传播步骤的限制。
由于过度平滑的问题，大多数现有的图神经网络只能通过其固有的有限聚合层来捕获受限的依赖关系。为了克服这个限制，本文提出了一种新的图卷积方法，称为图隐式非线性扩散（GIND），它可以隐式地访问无限跳的邻居，同时使用非线性自适应地聚合特征以防止过度平滑。
本文的主要贡献如下：
开发了一种新的隐式 GNN，即GIND。通过自适应地聚合来自邻居的非线性特征，它能够克服现有线性各向同性扩散的局限。 通过证明 GIND 的平衡状态对应于凸函数的解，为隐式 GNN 开发了第一个优化框架。基于这个观点，本文得出了三个具有经验优势的原则结构变体。 第三，通过减少输入图中的信息，GSAT 可以证明在某些假设下可以去除训练数据中的虚假相关性，从而实现更好的泛化。 在节点级和图级分类任务上的大量实验表明，本文的 GIND 在隐式 GNN 中获得了最先进的性能，并且与显式 GNN 相比也具有优势。
方法介绍
图隐式非线性扩散
鉴于现有基于线性各向同性扩散的隐式 GNN 的局限性，本文提出了一种新的非线性图扩散过程来设计隐式 GNN。此方法的非线性扩散可以自适应地聚合来自相似邻居的更多特征，同时分离不同的邻居。因此，它的平衡状态将保留更多的判别特征。
非线性扩散方程为本文使用线性算子 的非线性扩散使参数灵活化并获得可学习的聚合函数。
图上的非线性扩散方程将非线性扩散应用于图数据中并开发相应的隐式图神经网络。非线性扩散在图 上具有以下矩阵形式：
GIND的公式本文开发的新的隐式 GNN 具有以下公式：
GIND 的优化框架
受最近关于基于优化的隐式模型（Xie 等人，2022 年）的工作的启发，本文开发了第一个用于隐式图神经网络的优化框架。具体来说，GIND 的平衡状态对应于凸函数目标的解决方案。基于这一特性，可以通过各种正则化项推导出 GIND 的原则变体。隐式层的方程为：
GIND的高效训练
对于一般隐式模型以及隐式 GNN 来说，训练稳定性一直是一个广泛存在的问题。为了训练 GIND，本文采用了一种有效的训练策略，该策略在文章后面的实验中有效。
前向传播和反向传播计算在前向传播中，采用定点迭代。而在后向传播中，采用了最近开发的 Phantom Gradient 估算，该估算具有高效的计算和稳定的训练动态。
方差标准化对于 GIND，本文在非线性激活前应用归一化并丢弃均值项以使其保持符号保留变换：
实验分析
设计实验对 GIND 进行全面分析，并将其与隐式和显式 GNN 进行比较。
节点分类性能
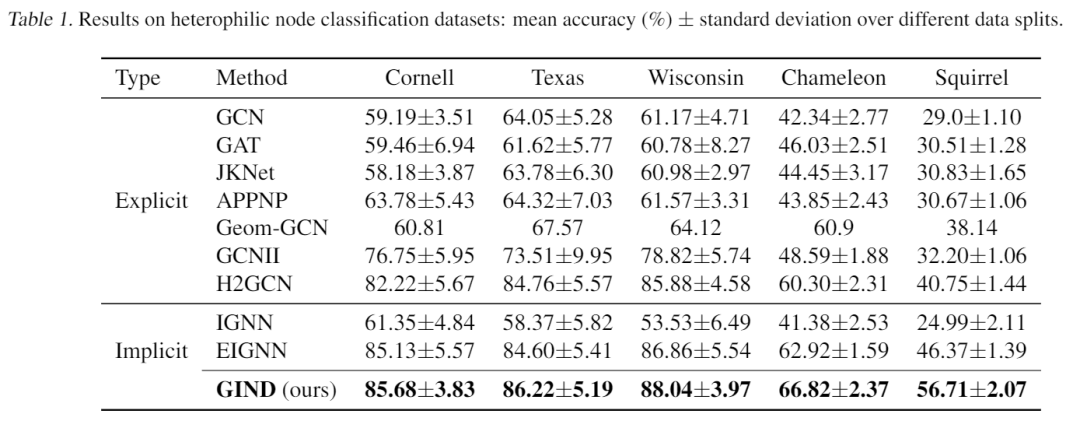如上表所示，GIND在所有异嗜性数据集上明显优于显式和隐式基线，尤其是在较大的数据集 Chameleon 和 Squirrel 上。
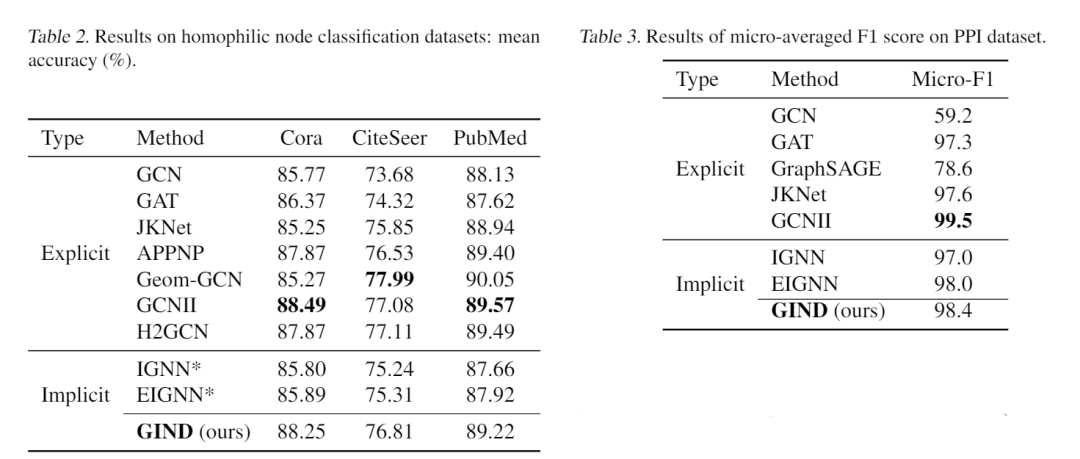此外，上表的结果表明，GIND 在 3 个引文数据集上实现了与比较方法相似的准确性。在 PPI 数据集上，如表 3 所示，GIND 达到了 98.4 的微平均 F1 分数，仍然优于其他隐式方法和大多数显式方法，接近最先进的模型。
图分类性能
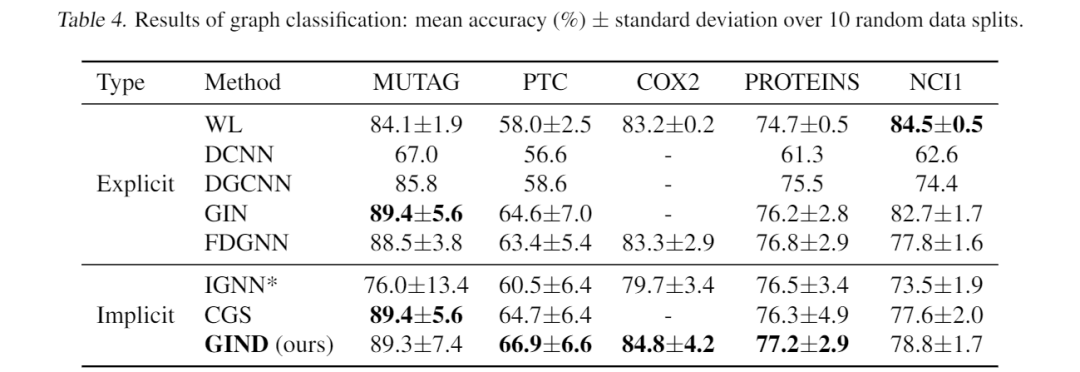在本实验中，GIND 在 5 个实验中的 3 个中取得了最佳性能。这能进一步验证了 GIND 的成功，它可以捕获长期依赖关系。
GIND的实证理解
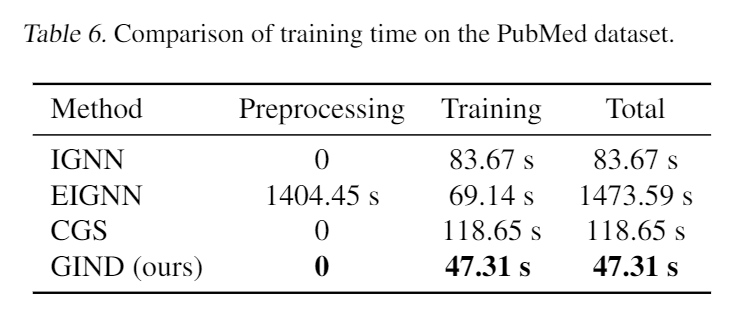如上表所示，与计算精确梯度的三个模型相比，本文提出的新模型花费的时间（47.31 秒）要少得多。在这三个模型中，EIGNN 是最有效的，训练成本为 69.14 秒，但其预处理成本远高于训练。
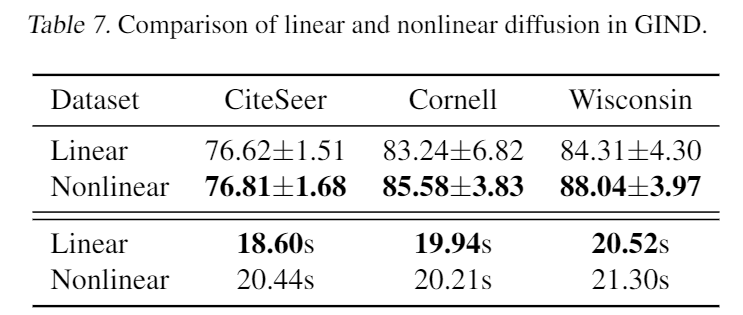从上表中，可以看到非线性扩散比线性扩散具有明显的优势，尤其是在异嗜性数据集上。同时，非线性设置带来的额外计算开销几乎可以忽略不计。
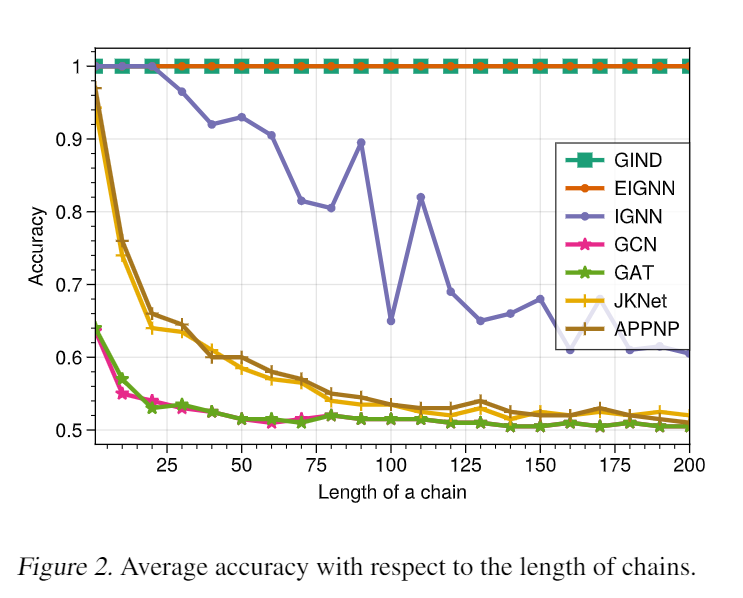上图显示了不同长度链的实验结果。一般来说，隐式模型都优于更长链的显式模型，验证它们在捕获远程依赖方面具有优势。GIND 和 EIGNN 都在长度为 200 的情况下重复保持 100% 的测试准确率。虽然 EIGNN 仅适用于线性情况，但 GIND 可以适用于更一般的非线性情况。
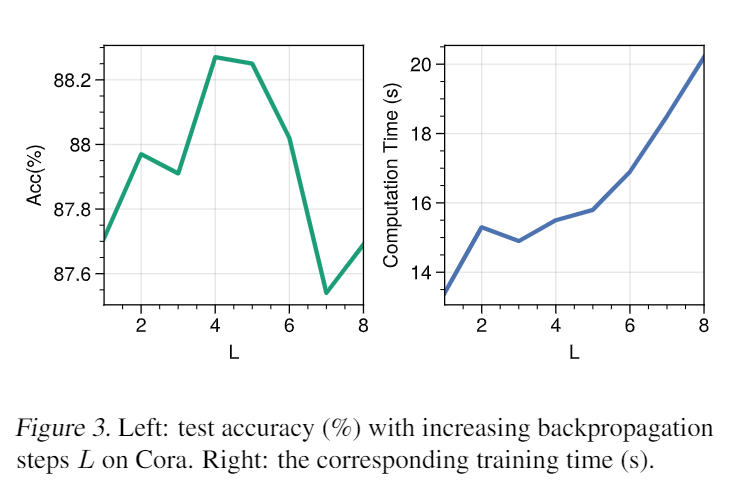上图中，将结果与 Phantom Gradient (Geng et al., 2021) 的不同反向传播步骤 以及它们在 Cora 数据集上的相应训练时间进行比较。可以看到有一个不同步骤之间的权衡， 太大或太小都会导致性能下降，最佳点在于 。相应的训练时间为 15.52 s，这仍然优于其他隐式 GNN（表 6）。
总结
本文开发了 GIND，这是一种优化诱导的隐式图神经网络，它可以访问无限跳的邻居，同时通过非线性扩散自适应地聚合特征。本文从优化的角度描述了隐式层的平衡，并表明学习的表示可以形式化为显式凸函数优化目标的最小化。受益于此，可以将先验属性嵌入到平衡中并引入跳跃连接以提高训练稳定性。大量实验表明，与以前的隐式 GNN 相比，本文提出的的 GIND 在各种基准数据集上获得了最先进的性能。
