同学们是不是在平常的开发工作中,只知道在查询慢的时候，会去考虑添加索引，建立索引可以有效的提高检索效率，但是有没有想过索引为什么提高检索效率？为什么MySQL的索引要用B+树，而不是二叉树、红黑树、Hash呢？看完这篇文章后你将对MySQL的索引有一个全面的认识。
索引的本质
MySQL官方对索引的定义为：索引（index）是帮助MySQL高效获取数据的数据结构（有序）。在数据之外，数据库系统还维护者满足特定查找算法的数据结构，这些数据结构以某种方式引用（指向）数据， 这样就可以在这些数据结构上实现高级查找算法，这种数据结构就是索引。如下图:
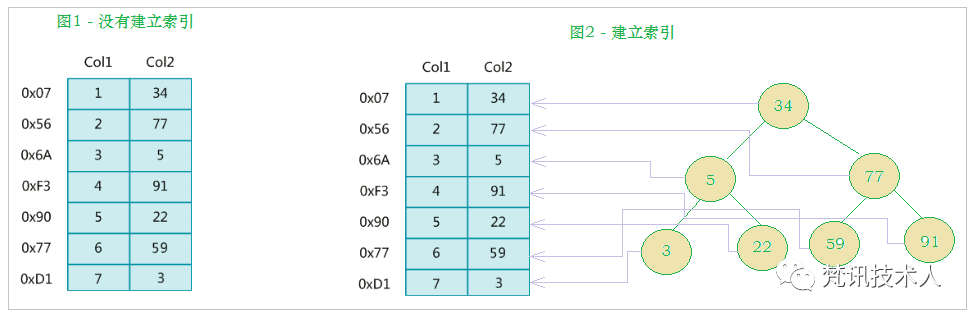
图1没有建立索引, 图2建立了索引,那么如果我们想要查找 col2 =59 的这一行数据, 这两种情况分别会怎么样查找呢？
1.没有建立索引，查找col2 =59 会进行全表扫描, 直到找完所有col2 =59的行2.建立了索引, 例如图2使用二叉树来存储了树结构, 查找col2=59就会是这样: 34=>77=>59,会进行3次磁盘IO。
可以明显的看到，建立了索引之后，可以有效的减少磁盘IO，提高检索的效率。
索引优势劣势
优势
1.类似于书籍的目录索引，提高数据检索的效率，降低数据库的IO成本。2.通过索引列对数据进行排序，降低数据排序的成本，降低CPU的消耗。
劣势
1.实际上索引也是一张表，该表中保存了主键与索引字段，并指向实体类的记录，所以索引列也是要占用空间的。2.虽然索引大大提高了查询效率，同时却也降低更新表的速度，如对表进行INSERT、UPDATE、DELETE。因为更新表时，MySQL 不仅要保存数据，还要保存一下索引文件每次更新添加了索引列的字段，都会调整因为更新所带来的键值变化后的索引信息。
磁盘存取原理
在具体讲索引结构之前,我们先来回顾一下磁盘存取原理。
1.磁盘整体结构示意图
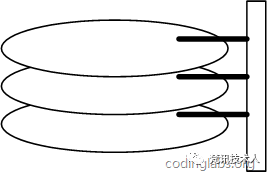
2.一个磁盘由大小相同且同轴的圆形盘片组成，圆盘可以转动，磁头可以沿磁盘半径方向运动(寻道)
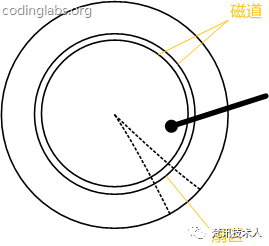
3.圆片被划分一系列同心圆，每个同心环叫做一个磁道，所有半径相同的磁道组成一个柱面。磁道被沿半径线划分成一个个小段，每个段叫做一个扇区4.为了读取这个扇区的数据，需要将磁头放到这个扇区上方，这个过程叫做寻道,花费时间叫做寻道时间，然后磁盘旋转将目标扇区旋转到磁头下，这个过程耗时叫旋转耗时。
其中寻道时间速度慢，而旋转时间速度快。那我们知道数据库的数据是存储在磁盘上的，那从下面这张表查找一行数据最坏的情况要经过7次磁盘IO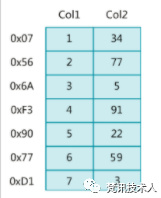
这样的话效率是非常低，所以这就是为什么要添加索引的根本原因。添加索引之后，可以精确的定位到想要查找的数据行的位置，有效的减少磁盘IO。
常用数据结构
在讲解常用数据结构之前，先给大家分享一个网站: https://www.cs.usfca.edu/~galles/visualization/Algorithms.html， 在这个网站上可以可视化的查看和操作各种数据结构。以下只是简单的回顾下常用的树结构，对这几种数据结构不清楚的可以先自学下。
二叉树
首先二叉树的定义是这样的：
1.任意节点左子树不为空,则左子树的值均小于根节点的值；2.任意节点右子树不为空,则右子树的值均大于于根节点的值；3.任意节点的左右子树也分别是二叉查找树；4.没有键值相等的节点；
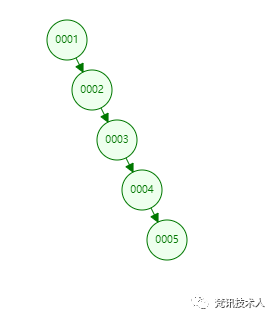如果我们想要查找的值是0005的话，那么就要经过5次磁盘IO。很显然，这种结构的树查询最坏的情况就会变成一个链表, 这样做很明显是不可取的。
红黑树(平衡二叉树)
•性质1：每个节点要么是黑色，要么是红色。•性质2：根节点是黑色。•性质3：每个叶子节点（NIL）是黑色。•性质4：每个红色结点的两个子结点一定都是黑色。•性质5：任意一结点到每个叶子结点的路径都包含数量相同的黑结点。
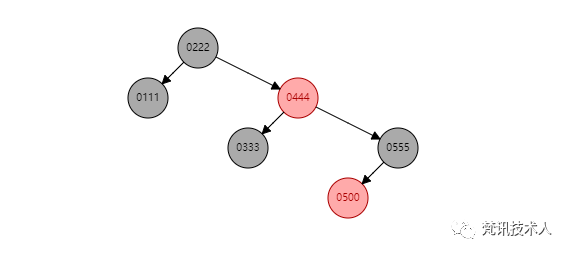
红黑树相对于二叉树在查找效率上已经优化很多了，那为什么MySQL不用红黑树呢？
假如我们的一张User表中有8条数据，如果用红黑树来存储索引,那这个树深度最大是3，如果有100万条数据，那么树的最大深度是: 2的n次方=100万，n就是树的深度,红黑树的深度是 O(logN)。
所以不采用红黑树作为索引的存储结构的原因是: 大数据量的情况下，采用红黑树存储会导致树的深度很大。树的每一层都代表一次IO，如果树的深度为n，那么它的IO次数为n，这也是不可取的。
B树
BTree又叫多路平衡搜索树，一颗m叉的BTree特性如下：
1.树中每个节点最多包含m个孩子。2.除根节点与叶子节点外，每个节点至少有[ceil(m/2)]个孩子。3.若根节点不是叶子节点，则至少有两个孩子。4.所有的叶子节点都在同一层。5.每个非叶子节点由n个key与n+1个指针组成，其中[ceil(m/2)-1] <= n <= m-1
B树示例
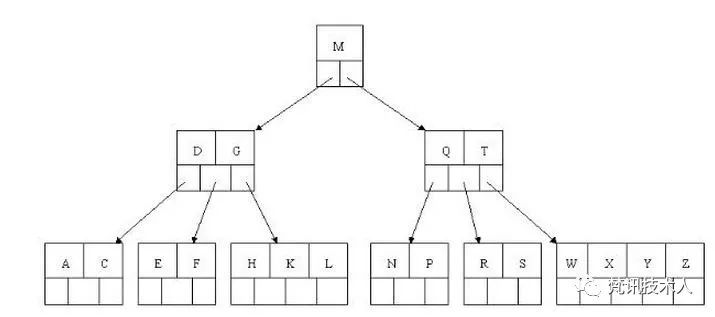
B树的查询流程
如上图我要从上图中找到E字母，查找流程如下
1.获取根节点的关键字进行比较，当前根节点关键字为M，E<M（26个字母顺序），所以找到指向左边的子节点（二分法规则，左小右大，左边放小于当前节点值的子节点、右边放大于当前节点值的子节点）；2.拿到关键字D和G，D<E<G 所以直接找到D和G中间的节点；3.拿到E和F，因为E=E 所以直接返回关键字和指针信息（如果树结构里面没有包含所要查找的节点则返回null）；
特点
B树相对于平衡二叉树的不同是，每个节点包含的关键字增多了，特别是在B树应用到数据库中的时候，数据库充分利用了磁盘块的原理（磁盘数据存储是采用块的形式存储的，每个块的大小为4K，每次IO进行数据读取时，同一个磁盘块的数据可以一次性读取出来）把节点大小限制和充分使用在磁盘快大小范围；把树的节点关键字增多后树的层级比原来的二叉树少了，减少数据查找的次数和复杂度;
MySQL的索引使用的是B+树,那为什么不用B树呢？B+树的优势是什么？请接着往下看。
B+树
B+树是B树的变种，它有以下几个特点:
1.非叶子节点不存储data,只存储key，可以提升度 (节点的数据存储个数)2.叶子节点不存储指针3.顺序访问指针，提高区间访问的性能
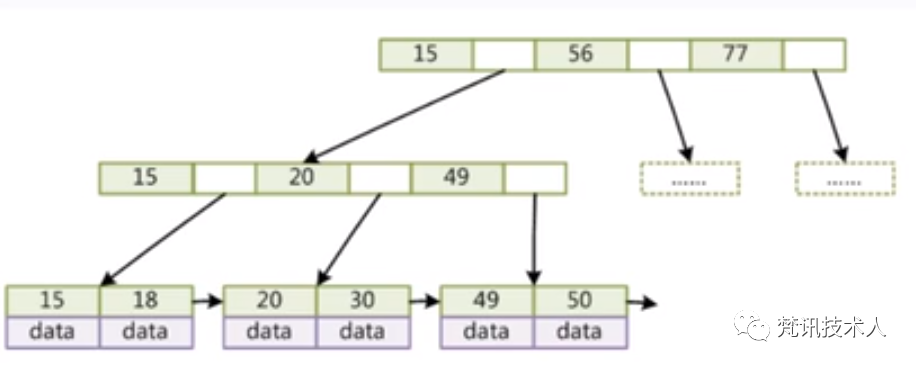
B+树相对于B树的优势
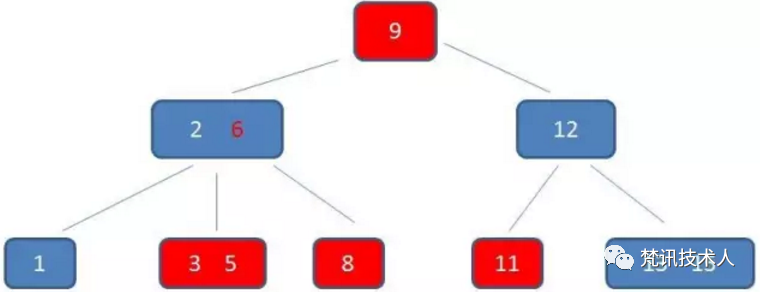
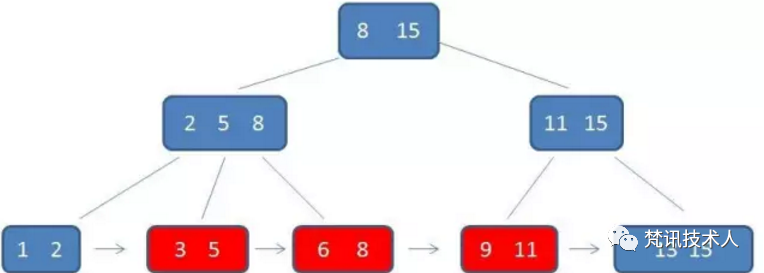
1.B+树的中间节点不保存数据，所以磁盘页能容纳更多节点元素。页是计算机存储器的逻辑块，页的大小通常为4K,如果在中间节点不保存数据，那么一页就可以保存更多的key,最终可以使得树的深度更小，磁盘的IO次数更少，查询效率更高。2.B+树查询必须查找到叶子节点，B树只要匹配到即可不用管元素位置，因此B+树查找更稳定（并不慢）；3.对于范围查找【WHERE col BETWEEN 1 and 2】来说，B+树只需遍历叶子节点链表即可，B树却需要重复地中序遍历，如下两图：
通过上面的讲解我们可以知道，非叶子节点不存储数据，只用来保存key，那是不是我的叶子节点保存的key越多，那最后形成的树的深度是不是越小呢？
答案是是的，但是MySQL对节点的保存key的最大值有一个限制，默认是16K，可以以下SQL查看配置:
SHOW GLOBAL STATUS like 'Innodb_page_size';复制
在讲解完B+树之后，以下几个问题就有了答案。
为什么MySQL页文件大小默认16K?
假设我们一行数据大小为1K,那么一页就能存16行数据，也就是一个叶子节点就能存16行数据；再来看非叶子节点，假设主键ID为bigint类型，那么长度为8B，指针大小在InnoDB源码中为6B，一共就是14B，那么一页里就可以存储16K/14=1170个(主键+指针)
那么一颗高度为2的B+树能存储的数据为: 117016=18720条，一颗高度为3的B+树能存储的数据为: 11701170*16=21902400(千万条), 所以在18720数据量下查找数据最多只需要2次IO, 在 21902400数据量下查找数据最多只需要3次IO。
为什么建议InnoDB使用int类型自增主键?
表的每一行记录必须要有一个唯一值来标识，在InnoDB中采用主键的规则:
如果我们定义了主键(PRIMARY KEY)，那么InnoDB会选择主键作为聚集索引、如果没有显式定义主键，则InnoDB会选择第一个不包含有NULL值的唯一索引作为主键索引、如果也没有这样的唯一索引，则InnoDB会选择内置6字节长的ROWID作为隐含的聚集索引(ROWID随着行记录的写入而主键递增，这个ROWID不像ORACLE的ROWID那样可引用，是隐含的)。
InnoDB的索引采用的是B+树，所以主键占用的字节数应该越小越好，这样就可以一次性读取到更多的KEY。
如果采用非自增主键，由于每次插入主键的值近似于随机，因此每次新记录都要被插到现有索引的中间某个位置，此时MySQL不得不为了将新记录插到合适位置而移动数据，甚至目标页面可能已经被回写到磁盘上而从缓存中清掉，此时又要从磁盘上读回来，这增加了很多开销，同时频繁的移动、分页操作造成了大量的碎片，得到了不够紧凑的索引结构，后续不得不通过OPTIMIZE TABLE来重建表并优化填充页面。
在索引排序的过程中，int排序相对于字符串、UUID等类型的排序相对要快一点。
所以，在建表时建议使用int类型作为自增主键。
总结
1.索引（index）是帮助MySQL高效获取数据的数据结构（有序）。2.建立索引的目的，可以有效的减少磁盘IO，提高检索的效率。3.磁盘访问效率远低于内存访问效率，要尽量减少磁盘IO。4.使用二叉树或红黑树可能会导致树的深度很大，导致磁盘IO次数增加。5.B树重要的特征是每个节点包含多个孩子。6.B+树相对于B树的优势主要是，非叶子节点存储key，叶子节点存储data，叶子节点之间使用链表链接,用来提升范围查询效率。
参考资料
1.https://tech.meituan.com/2014/06/30/mysql-index.html2.https://www.cnblogs.com/dylan123/articles/13061152.html3.https://zhuanlan.zhihu.com/p/27700617
