
点击蓝字关注我们
MATLAB是美国mathworks公司出品的商业数学软件,其被广泛应用于许多行业领域。今天,小编就带大家一起了解一下simulink仿真的自衡过程吧。
01
过程描述
系统由一个水箱、控制水流流入的调节阀、控制水流流出的负载阀组成。
由水箱的传递函数表达式可知,水箱系统为一个一阶惯性环节,其单位阶跃响应为一个单调递增的函数曲线,故系统的超调量大,响应时间长,需较长一段时间才能达到稳态。
针对水箱系统的以上特点,在系统中加入PID控制器,通过理论计算法确定控制器参数,构建新的水箱液位控制系统。
PID控制器通过积分环节消除误差,而微分环节可缩小超调量、加快系统响应,理论上可以使系统具有一个良好的动态性能及稳态性能。
02
工具
装有win10系统的电脑一台,
Matlab_ R2021a(64bit)软件。(小编用的是这个)
03
操作过程
(1)双击Library Browser,如图3.1所示。
图3.1 打开simulink库
(2)于库中寻找所需的模块,搭建如图3.2所示回路。
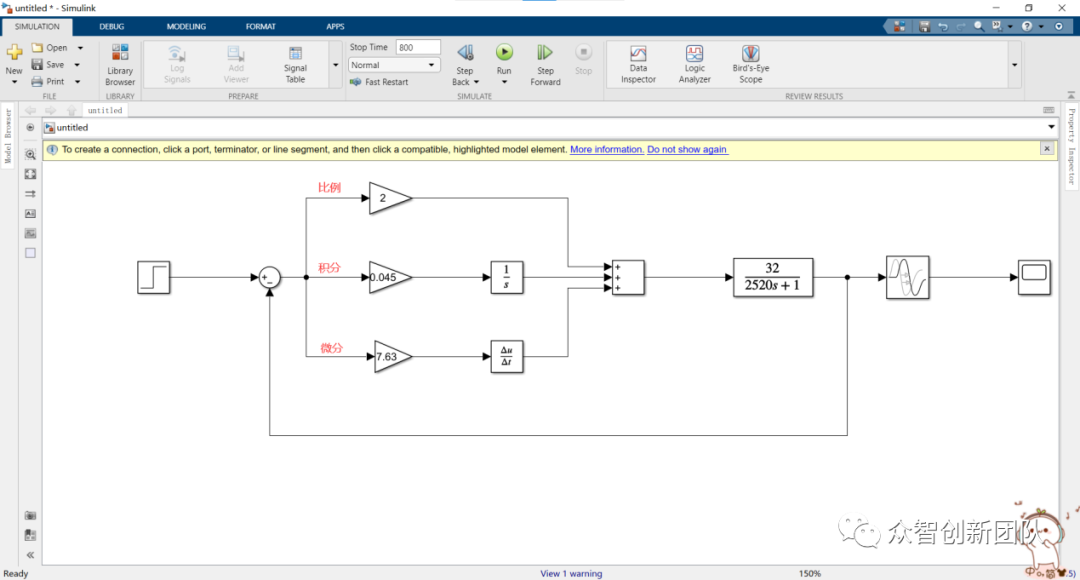
图3.2 搭建回路
其中,比例,积分,微分任意给一些值。(小编给的是2 , 0.045 , 7.63)
(3)对自衡单容过程的分析,曲线如图3.3所示。
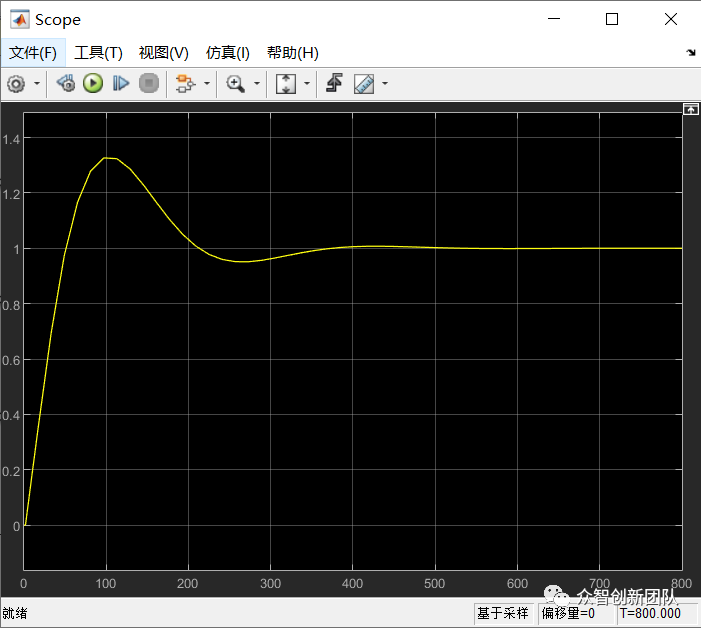
图3.3 液位曲线

分析
<1>随着静态过程增益的增加,系统的余差减小,最大偏差减小,“控制作用增强,但稳定性变差。
<2>在其他因素相同的条件下,如果过程静态增益越大,则控制作用就越大,克服扰动的能力也越强。
<3>对于扰动通道的增益,在其他因素相同的条件下,增益越大,系统余差越大,最大偏差也越大。

最后附上一些调节pid的方法规律。
(1)一般来说,在整定中,观察到曲线震荡很频繁,需把比例带增大以减少震荡;当曲线最大偏差大且趋于非周期过程时,需把比例带减小。
(2)当曲线波动较大时,应增大积分时间;曲线偏离给定值后,长时间回不来,则需减小积分时间,以加快消除余差。
(3)如果曲线震荡得厉害,需把微分作用减到最小,或暂时不加微分;曲线最大偏差大而衰减慢,需把微分时间加长而加大作用。
(4)比例带过小,积分时间过小或微分时间过大,都会产生周期性的激烈震荡。积分时间过小,震荡周期较长;比例带过小,震荡周期较短;微分时间过大,震荡周期最短。
(5)比例带过大或积分时间过长,都会使过渡过程变化缓慢。比例带过大,曲线如不规则的波浪,较大地偏离给定值。积分时间过长,曲线会通过非周期的不正常途径,慢慢回复到给定值。
注意:当积分时间过长或微分时间过长,超出允许的范围时,不管如何改变比例带,都是无法补救的。


 点个“分享”吧!
点个“分享”吧!







