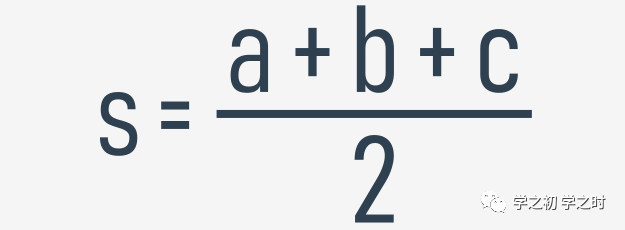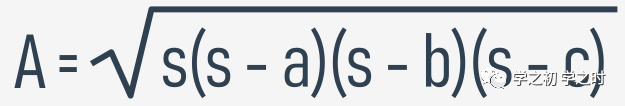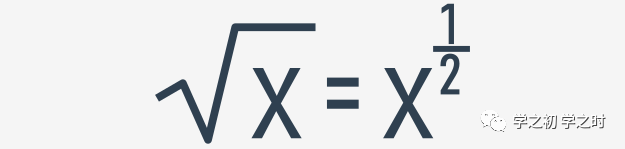例子一涉及到的是三角形和勾股定理的知识,先来简单回顾一下:
「例子一解决的问题是:检查给定长度的三条边是否可以构建一个直角三角形。」
def is_a_triangle(a, b, c): return a + b > c and b + c > a and c + a > bprint(is_a_triangle(5, 3, 4)) #输出:Trueprint(is_a_triangle(1, 3, 4)) #输出:Falsedef is_a_right_triangle(a, b, c): if not is_a_triangle(a, b, c): return c ** 2 == a ** 2 + b ** 2 return a ** 2 == b ** 2 + c ** 2 return b ** 2 == a ** 2 + c ** 2print(is_a_right_triangle(3, 5, 4)) #输出:Trueprint(is_a_right_triangle(1, 3, 4)) #输出:False
首先我们来看例一给出的两点信息:
- is_a_triangle(a, b, c)的主体内容是「判定是否为三角形:所有两边之和均大于第三边的为三角形」
- is_a_right_triangle(a, b, c)的主体内容是「判定是否为直角三角形:勾股定理」
首先,我们需要思考——在什么条件下三条边可以构建一个三角形?答案是:给定三边边长a、b、c,两两相加之和均大于第三边时,可证明该三边可构建为一个三角形。因此,is_a_triangle(a, b, c)这个function所做的事情是「定义三角形」。而code所表达的意思是:「a + b > c, b + c > a,c + a > b这三个条件都成立,a、b、c可构建一个三角形,而return放这里可以理解为“我准备好了,请召唤我吧!”。」function外的print(is_a_triangle(5, 3, 4)) 和 print(is_a_triangle(1, 3, 4))即为“召唤”。is_a_right_triangle(a, b, c)这个function所做的事情是「定义直角三角形」。而code所表达的意思是:「首先判定是不是三角形,如果不是,就return False,根据勾股定理,最长边的平方等于另外两边分别平方相加之和,即为直角三角形」。最后,print(is_a_right_triangle(3, 5, 4))符合a + b > c and b + c > a and c + a > b也符合elif b > a and b > c两个条件,为直角三角形,所以输出为True;
print(is_a_right_triangle(1, 3, 4))不符合a + b > c,即不符合构建三角形的条件,也就不需要看是不是直角了,所以输出为Fasle。
理解了三角形的定义,我们再来看,确定是三角形之后,我们如何编程出「求解三角形面积」的function。先来回顾一下数学里的三角形求解面积的公式——海伦公式:公式中,S表示周长的一半(例子二中由p表示),A表示面积。def is_a_triangle(a, b, c): return a + b > c and b + c > a and c + a > b return (p * (p - a) * (p - b) * (p - c)) ** 0.5def area_of_triangle(a, b, c): if not is_a_triangle(a, b, c):print(area_of_triangle(1., 1., 2. ** .5))
其实知道三角形面积数学上的求解公式,def function就完成了一半,所以不再陈述例子二的coding剖析,只提以下几点:
- 和确定是否为直角三角形一样,求解三角形面积,首要任务也是「判断是否为三角形」
- 公式中的根号则用**0.5来表示,因为
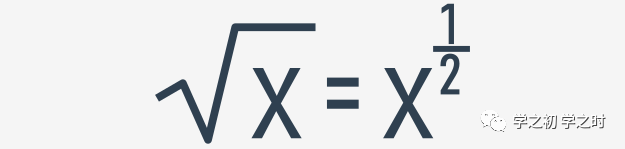
- 例子二coding的结构是:①def判断三角形的function ②def求解三角形面积的function ③ def最终输出的function (输出为none或者面积)
- print(area_of_triangle(1., 1., 2. ** .5))中,1.实际指1.0,2.**.5指2.0的0.5次方
阶乘的百度定义是:一个正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,并且0的阶乘为1,自然数n的阶乘写作n!。##阶乘定义(不要与Python中的 !=“不等于”混淆)n! = 1 * 2 * 3 * 4 * ... * n-1 * ndef factorial_function(n): for i in range(2, n + 1):for n in range(1, 6): # testing print(n, factorial_function(n))
对于例子三,需要提一点的是——function内部的for loop是核心,以 product = 1 for i in range(2, 5): product *= i 为例,其引发的输出可参考下面的模式:
①range(2, 5)指的是整数2,3,4,也就是说for i in [2, 3, 4]②电脑在loop中的「运算思路」是这样的:i == 2, product = 1*2 = 2;i == 3, product = 2*3 = 6;i == 4, product = 6*4 = 24③function外的for loop就是以function本身的规律进行计算,最终得出结果斐波纳契数列的百度定义是:又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)。我是这样理解的:三个数为一组,第三个数 = 第一个数 + 第二个数,也就是「从这个数列第3项开始,每一项都等于前两项之和」。
咋一看例子四,我看到了「元素对换」elem_1, elem_2 = elem_2, the_sum(戳list内元素对换和sort这一期)。
for i in range(3, n + 1): the_sum = elem_1 + elem_2 elem_1, elem_2 = elem_2, the_sumfor n in range(1, 10): # testing
此外,最难理解的大概就是function内for loop这里,我们来一探究竟:
①当n == 6, for i in range(3, n + 1) 即为 for i in [3, 4, 5, 6]②电脑在loop中的「运算思路」是这样的 (图1):
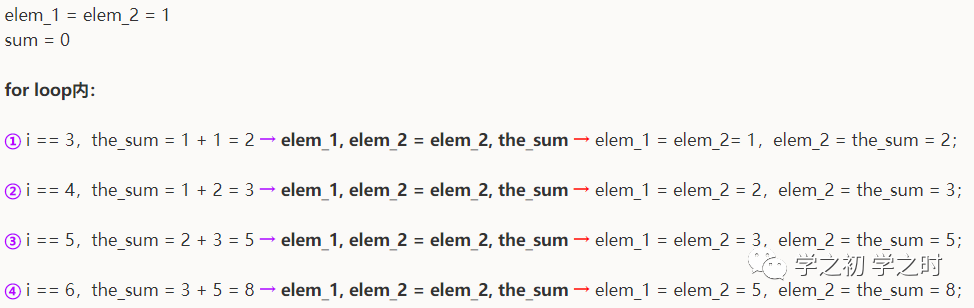
也就是说,当i == 4时,求the_sum = elem_1 + elem_2用的值其实是当i == 3时,elem_1和 elem_2的值。也就是将fib_4中的1和2分别和2和3进行交换,因此得到原位置的1变成2,原位置的2变成了3,2 + 3 正好等于fib_5等式的结果5。递归的百度定义是:在运行的过程中调用自己,递归关系就是实体自己和自己建立关系。刚才讲的阶乘和斐波纳契数列是典型的递归案例。定义中说的自己和自己建立联系,用斐波纳契数列,我如此理解:fib_4 = 1 + 2 = 3和fib_5 = 2 + 3 = 5中的2就是自己。在编程领域中,递归是一种function函数调用自身的技术。根据 Fibi = Fibi-1 + Fibi-2 ,上面讲斐波纳契数列的例子四也可由下面简便的例子五替代,毕竟元素换来换去很绕。以i == 4为例,也就是说Fib4 = Fib3 + Fib2
由fib_2 = 1, fib_3 = 1 + 1 = 2 和fib_4 = 1 + 2 = 3可知fib_4 = fib_3 + fib_2,所以上述有道理。
return fib(n - 1) + fib(n - 2)
同理,上面讲阶乘的例子三也可由下面简便的例子六替代。
def factorial_function(n): return n * factorial_function(n - 1)for n in range(1, 6): # testing print(n, factorial_function(n))
例子五和例子六都采用了十分直接的coding模式,简便的方式却能产生风险,比如如果你忘记考虑「可以停止递归invocations调用链的条件」,程序可能会进入无限循环,所以必须小心。
今天的分享就到这里了,感谢学习路上的你我TA!