
作者 | bisonliao
导读
用了这么久的Java基础数据类型,但浮点数精度问题产生原因是什么?BigDecimal又是怎么解决精度问题的?Bison大神这篇文章将带你一窥究竟。
Java码农做金融,就不得不说double与BigDecimal数据类型。本小文通过简单的例子直观的介绍double数据类型引入的误差和BigDecimal解决方案。
双精度浮点数,即double precision floating-point format,是计算机中普遍使用的64 bit的数字格式,也普遍的出现在C/C++、Fortran、Java、JavaScript等程序语言中,后文中会简称double类型。对应的还有32 bit的单精度浮点数。他们遵从IEEE 754标准系列。
1 double类型的内存格式
详尽的文档,可以参考IEEE 754文档或者double数据类型的wikipedia词条。这里用一个小例子展示一下double类型的内存格式。
1.1 先说数学上的进制转换
以十进制小数 13.3125为例,转化为二进制表示就是1101.0101。
十进制小数,小数点左边依次表示1、10、100、…,小数点右边依次表示1/10、1/100、1/1000,…。类比之下,二进制小数的小数点的左边的依次是1、2、4、8、…,小数点右边依次表示1/2、1/4、1/8、…。
所以1101.0101的小数部分就是1个1/4加上1个1/16,即5/16=0.3125;而整数部分就是1个1+1个4+1个8,即13。
将十进制小数转二进制小数的手工计算方法,需要对整数部分和小数部分分开处理:
小数部分,不断的将十进制小数的小数部分乘以2,得到的积的整数部分就依次是二进制小数的小数部分的bit位,不断远离小数点的方向:
0.3125 X 2 = 0.6250 ------ 0
0.6250 X 2 = 1.25 ------ 1
0.25 X 2 = 0.5 ------ 0
0.5 X 2 = 1.0 ------ 1
所以0.3125的二进制表示是 0.0101复制
整数部分,就是不断的除以2,得到的余数就是二进制表示的bit位,不断远离小数点的方向:
13 / 2 = 6 余 1 ----- 1
6 / 2 = 3 余 0 ----- 0
3 / 2 = 1 余 1 ----- 1
1 / 2 = 0 余 1 ----- 1
所以13的二进制表示是 1101复制
1.2 再说double类型的内存格式
先看一张来自wikipedia上该词条的图片:
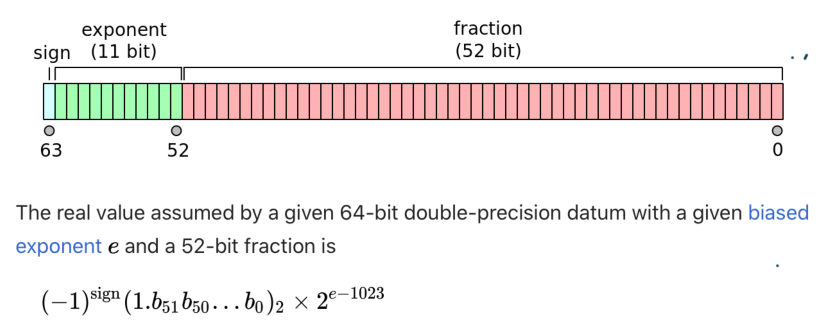
还是以十进制小数 13.3125为例,转化为二进制表示就是1101.0101。
第一步,通过小数点移位,使得整数部分为1,并明确正负号:
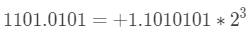
第二步,指数部分(也就是十进制3)加上1023,
指数部分:3+1023 = 1026,即二进制 100 0000 0010复制
指数部分为什么要这样处理呢,因为double类型用11bit整数存储指数,取值范围为 [0, 2017],而指数可正可负,所以有个偏移1023, [0, 2017] 依次映射到 [-1023, 1024]。
第三步,依次填入1位符号位、11位指数、52位小数部分:
0,100 0000 0010, 1010 1010 0...0复制
如果是-13.3125,则:
1,100 0000 0010, 1010 1010 0...0复制
写段代码验证一下:
int main()
{
double number = -13.3125;
unsigned char* p = (unsigned char*)&number;
int len = sizeof(double);
//先高字节,再低字节
for (int i = len-1; i >= 0; --i)
{
//先高bit再低bit
for (int j = 7; j >=0; --j)
{
printf("%d", (p[i] >> j)&1);
if (4 == j)
{
printf(" ");
}
}
printf(" ");
}
return 0;
}
//输出为:
1100 0000 0010 1010 1010 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000复制
IEEE 754标准没有对字节序做明确规定,所以在不同的cpu上面,浮点数的表示可能会有差异。详细可以参考一下/usr/include/ieee754.h文件。
2 double类型的误差
由于实数是连续且无穷多的,任意两个不相等的实数之间都有无穷多个实数。而double使用64 bit 有限个数的状态(虽然这个状态个数也是巨大的)来表示实数,庄子说:“以有涯随无涯,殆已!”,所以使用double一定会引入误差。
任意两个连续的double内存状态之间有无穷多个实数,如果运算结果落在其中的某个实数,double就只能用附近的这两个状态中的一个来表示,误差由此产生了。而且越靠近实数轴的两侧,误差越大。
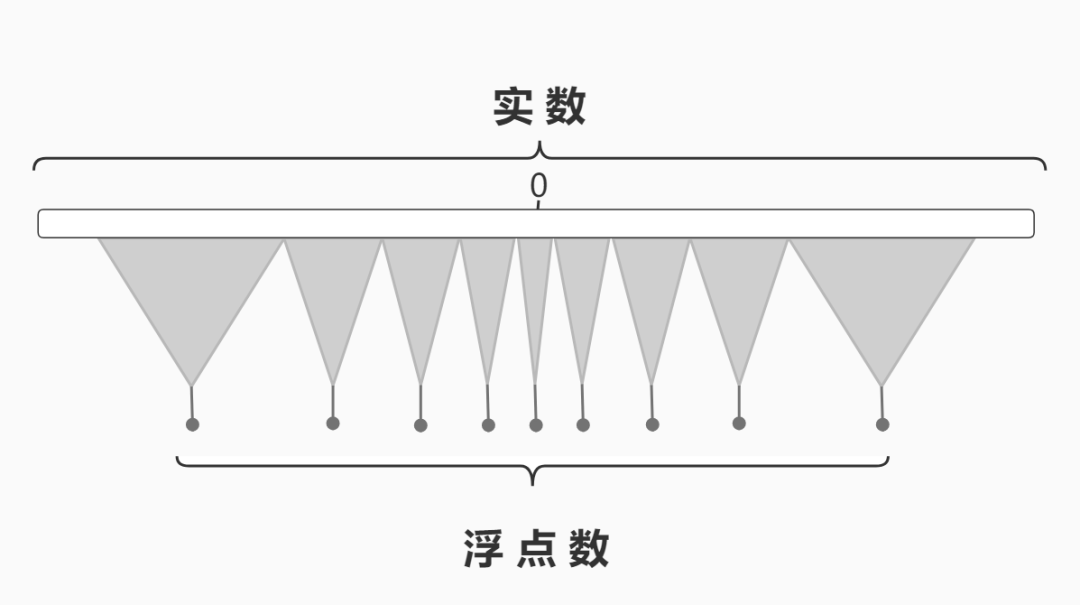
根据前面的例子可以看出,只有小数部分能拆解为1/2、1/4、1/8、…、这些有理数的和的实数才可以被double准确的表示,例如:
0.015625 = 1/64
0.876953125 = 1/2 + 1/4 + 1/8 + 1/512复制
如果不能分解为1/(2^n)的和的形式,即使看起来特别“正常”的一个小数,也不能被double准确的表示,0.1 到 0.9 的 9 个小数中,只有 0.5 可以用浮点数准确表示!例如:
0.7(十进制) = 0.10 1100 1100 ...(二进制) //不断的1100循环出现复制
一小段代码验证一下:
int main()
{
double number = 0.7;
unsigned char* p = (unsigned char*)&number;
int len = sizeof(double);
//先高字节,再低字节
for (int i = len-1; i >= 0; --i)
{
//先高bit再低bit
for (int j = 7; j >=0; --j)
{
printf("%d", (p[i] >> j)&1);
if (4 == j)
{
printf(" ");
}
}
printf(" ");
}
printf("\n");
printf("%f\n", number);
printf("%.100f\n", number);
printf("%.50f\n", number);
printf("%.30f\n", number);
return 0;
}复制

可以看到,具体到0.7这个数,double引入的误差的绝对值相当的小。但如果一个数的整数部分就占用了很多有效数字,那么小数部分的误差绝对值可能就会比较大。也就是说,表示的原值的绝对值越大,double越不精确!
例如,把上面代码里的number值改为123456123456.7,就会得到这样的输出:

可以看到,double的有效数字的位数是(很)有限的(52 bit),如果原值的整数部分很大,那么留给小数部分的有效数字就很少了,误差的绝对值(0.000003)比前面0.7的例子大了很多。
进一步的,当原值的绝对值进一步加大的时候,连整数部分也不准确了。
例如,把上面代码里的number改为123456123456123456123.7, 输出为:
123456123456123453440.0000000复制
在实际工作中,如果使用double类型表示金额和利率(例如利率0.7),虽然单次的误差可能不太大,但随着运算复杂度的增加,引入的误差可能会叠加,而且随着原值的绝对值增大,误差也会增大,不能确保小数点后2位一定是精确的(金额里的通常单位“分”所在的位置)。
不过可以明确的一点是,在Java或者C/C++语言中,int类型的数据转化为double的时候,是不会有精度损失的,因为int类型的数的绝对值相对double来说不大,double有足够的有效数字位数来保证它的精度。
3 BigDecimal
这个问题通常的解决方案,是使用其他更精确的数据类型替代double。
例如在 Java中,可以使用BigDecimal类。BigDecimal的实现原理,可以简单理解为:其内部使用如下方式来表示一个实数: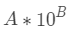
其中A是BigInteger,一个任意精度的大整数,B是一个int类型。
例如实数 13.3125, BigDecimal内部就表示为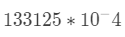
当然,在实际实现的时候,BigDecimal有一些优化,例如A可以用一个long保存的话就保存为long。
加减乘除四则运算,就按算术直观的算法进行,例如加法,两个数先对齐B,然后A相加。
在初始化BigDecimal实例的时候,通常传入字符串方式的精确原值,避免编译器对常量实数先转化为double而损失了精度。
BigDecimal是一个常量类,例如加法 x.add(y) 不会改变x本身,而是返回一个新的BigDecimal实例作为结果。
详细可见BigDecimal的源码:
https://github.com/frohoff/jdk8u-dev-jdk/blob/master/src/share/classes/java/math/BigDecimal.java复制
类似的高精度的数学库还很多,例如支持任意精度的数学库GMP,官网:
https://gmplib.org/复制
复制
end







