并查集概述
并查集主要解决两个节点之间是否连接问题,而不关心具体连接的路径.基本所有的数据的结构只是针对特定的问题,有着高效的运行时间
如图
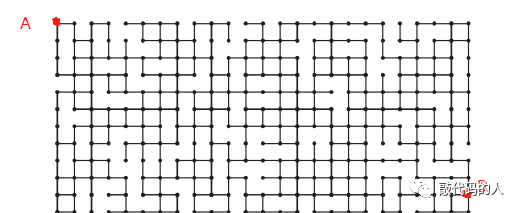
在并查集中,只关系A和B是否连接,而不关心它们之间的路径(怎么连接)
并查集的设计:
对于一组数据主要支持两个动作:
union(p,q) 把这两组数据并起来
isConnected(p, q)判断这两组数据是否连接
接口的设计
public interface UF {//获取并查集中元素的个数int getSize();//给定两个集合的索引,关心的是他们的集合是否连接//而不关系集合的具体内容//所以对于并操作,传入的是索引void unionElements(int p, int q);//同理判断两个集合是否连接boolean isConnected(int p, int q);}复制
并查集基本数据表示
图一:

图二:

判断两个元素是否连接,只需要判断他们所对应id值是否一样.id是一个数组,里面存放的是元素之前连接的的标识.就是相同的数字.而元素相当于集合的索引.
判断连接问题只需要判断find(p) == find( q)就是find(0)是否等于find(2)
用数组实现具体的并查集
基础框架设计:
public class ArrayUnionFind implements UF {// 内部私有一个数组,存放每个元素对应所属集合的编号private int[] id;// 有参构造public ArrayUnionFind(int size) {// 对于id的初始化id = new int[size];// 对于每一个元素的初始化// 可以理解为所有元素一开始都是分开的for (int i = 0; i < id.length; i++) {id[i] = i;}}public int getSize() {return id.length;}}复制
连接两个元素的方法:
思路分析:
获取两个元素对应集合的id值
判断id值是否一样,一样说明已经连接,直接放回
不一样,把一个元素所对应集合的id全部改成另一个元素所对应的集合的id
// 设计辅助方法.获取对应元素集合的idprivate int find(int p) {// 判断索引的有效性if (p < 0 || p > id.length) {throw new IllegalArgumentException("p is out of bound");}//返回对应的idreturn id[p];}//连接两个元素public void unionElements(int p, int q) {//或者对应的集合编号int PID = id[p];int QID = id[q];//如果相等,说明已经连接,直接返回if(PID == QID){return;}//遍历整个数组把所有属于PID的元素,全部转换为QIDfor(int i = 0; i < id.length;i++){if(id[i] == PID){id[i] = QID;}}}复制
判断是否连接:
//判断两个元素是否连接public boolean isConnected(int p, int q){//其实就是查找存储它们的id值return find(p) == find(q);}复制
并查集树结构的表示方法:
如图(是动态图,有点慢)

具体实现思路:
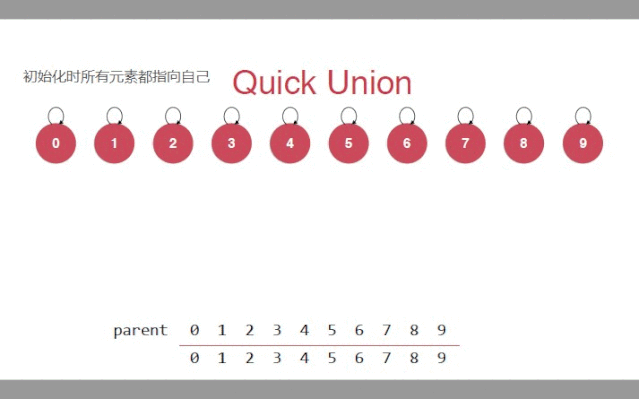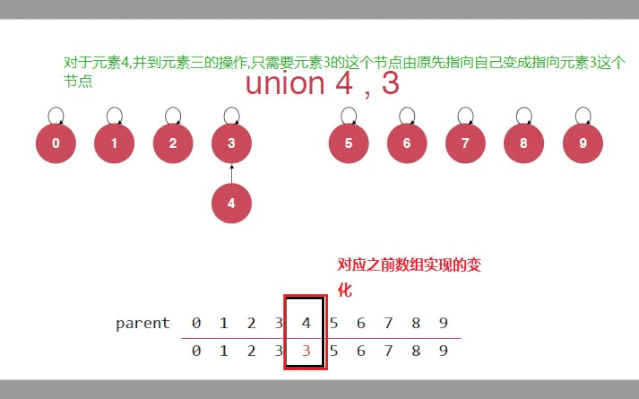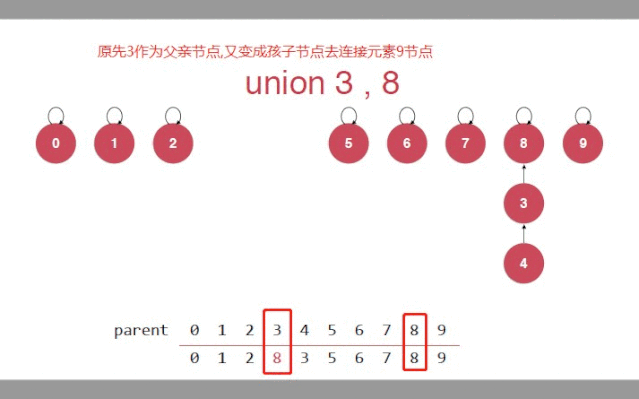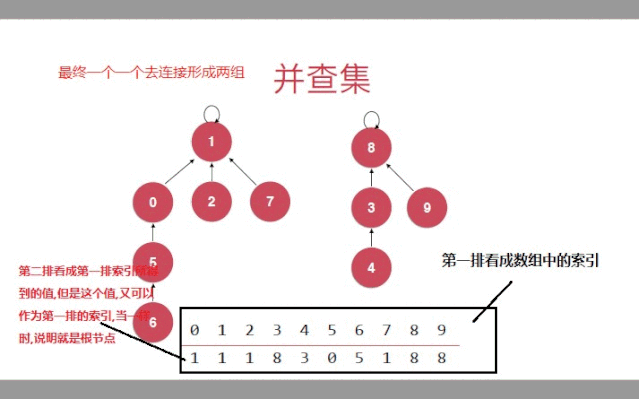
是个由孩子指向父亲的的树,但是还是数组保存,只是保存的规则展开就是树的表示形式
初始化时,每一个节点都是单独的一个节点
当合并时,一个元素作为孩子节点指向另一个元素节点(作为父亲节点)
第二句话在数组中的理解就是,第一个元素作为索引,查出来的值,就是第二个元素所连接的值
父亲节点又可以作为孩子节点,去连接别的节点
第四句在数组中的解释,查出来的值,又可以作为索引(孩子)去查另外的值(父亲)
如果这个值作为索引,查出来的还是自己,说明就是根节点.数组中,就是索引和值一样
现在判断两个元素是否连接,不能像之前的数组一样,只取所对应集合的id,而是要遍历到根基点,判断两个两个元素的根节点是否一样,就是索引和值一样
换句话说,找根节点的方法就是索引找到值,值又当索引找值,直到索引和值一样
动态图辅助理解
树结构的并查集设计
public class TreeUnionFind implements UF{//定义数组存放父亲节点private int[] parent;//初始化public TreeUnionFind(int size) {parent = new int[size];//初始化,让每个节点都指向自己//数组中就是索引和索引中对应的值相等for(int i = 0; i < parent.length;i++){parent[i] = i;}}//获取元素的个数public int getSize() {return parent.length;}//设计私有方法;查询一个节点(索引)的根节点private int find(int p){//判断索引的有效性if(p < 0 || p >= parent.length){throw new IllegalArgumentException("p is out of bound");}//数组中对应索引的值(父亲节点),它又作为新的索引去寻找父亲//当索引和找到的父亲一样时,就是自己指向自己,就是根节点while(p != parent[p]){p = parent[p];}return p;}//合并操作p,和q//只需要p的根节点指向q的根节点public void unionElements(int p, int q) {//找到p,和q所在的根节点int pRoot = find(p);int qRoot = find(q);if(pRoot == qRoot){return;}//p的根节点本来是parent[pRoot],还是自己//现在指向q的根节点parent[pRoot] = qRoot;}public boolean isConnected(int p, int q) {return find(p) == find(q);}}复制
并查集优化
基于size的优化
问题分析:
对于使用树结构使用并查集时,对于UnionElements(int p, int q),这个操作,总是把p所在元素的根节点直接指向q所在元素的根节点
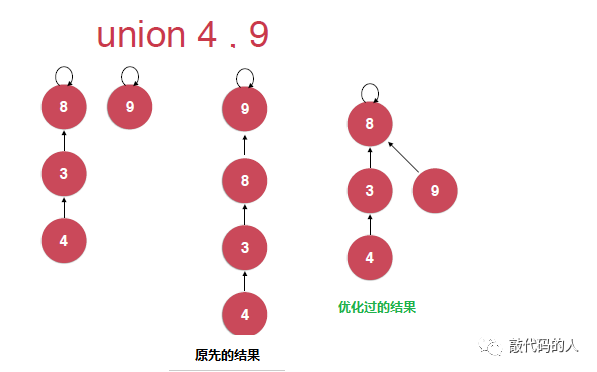
如果每次q本身就是根节点(就是一个元素),我们每次都把p指向q,那么这棵树就会编程一个单链表,查询复杂度是一个o(h),就会接近o(n)
解决方案:
可以把元素个数少的那棵树指向元素个数多的那棵树,这样可以避免树越来越长
定义要给数组size[p],存放以p为根节的集合元素的个数(就是这棵树的个数)
代码实现
public class TreeSzieUnionFind implements UF {// 定义节点存放父亲节点private int[] parent;// 存放以根为索引的值(就是元素个数)private int[] sz;// 定义构造方法public TreeSzieUnionFind(int size) {for (int i = 0; i < size; i++) {// 初始化,每个节点的父亲都是自己parent[i] = i;// i就是父亲节点,每棵树只有一个元素sz[i] = 1;}}public int getSize() {return parent.length;}// 寻找父亲节点,一样的设计private int find(int p) {if (p < 0 || p > parent.length) {throw new IllegalArgumentException("p is out of bound");}while (p != parent[p]) {p = parent[p];}return p;}// 合并操作p,和q// 只需要p的根节点指向q的根节点public void unionElements(int p, int q) {int pRoot = find(p);int qRoot = find(q);if (pRoot == qRoot) {return;}// 元素p所在根节点,所挂的元素个数,小于qif (sz[pRoot] < sz[qRoot]) {// 让p指向qparent[pRoot] = qRoot;// 维护一下q所在根节点的拥有元素的个数sz[qRoot] += sz[qRoot];} else {parent[qRoot] = pRoot;sz[qRoot] += sz[pRoot];}}public boolean isConnected(int p, int q) {return find(p) == find(q);}}复制
基于rank的优化
基于size优化的问题分析
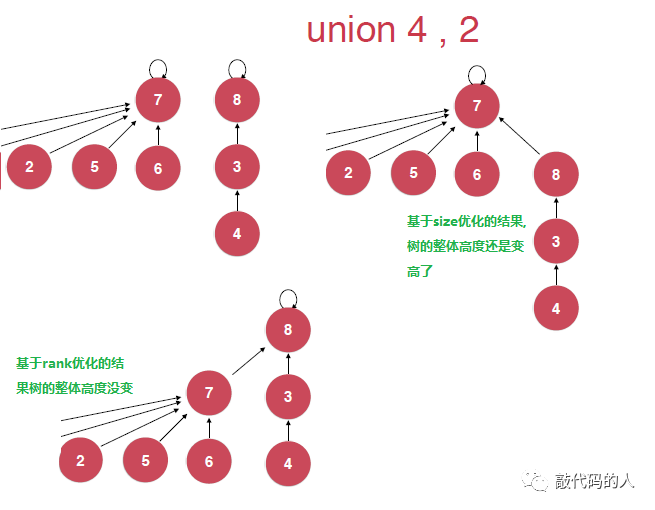
如果有五个孩子同时指向要给父亲,那么那么这棵树的个数就是6
但是如果有一个a指向b,b指向c的这颗树,他的个数是3
合并时,会把少的直接挂接到多的上去
但是问题时原本个数6的这个树的高度只有2,二个数3的这个树的高度有3
如果基于size优化的话,整体树的高度还是变成了4,不利于查询
解决方案
如出现上述两棵树,我们可以把低树(高度低)合并到高棵树上,这样整体rank就不会变
定一个数组rank,记录根节点所对应这棵树的高度的优先级
合并时,底树指向高树
public class TreeRankUnionFind implements UF {// 定义节点存放父亲节点private int[] parent;// 存放以根为索引的值(就是这棵的高度优先级)private int[] rank;public TreeRankUnionFind(int size) {for (int i = 0; i < size; i++) {// 初始化,每个节点的父亲都是自己parent[i] = i;rank[i] = 1;// 初始化时,i就是父亲节点,每棵树的高度就是1}}// 实现方式一样private int find(int p) {}@Overridepublic int getSize() {// TODO Auto-generated method stubreturn 0;}@Overridepublic void unionElements(int p, int q) {int pRoot = find(p);int qRoot = find(q);if(pRoot == qRoot){return;}//pRoot根节点的高度小于qRoot根节的高度if(rank[pRoot] < rank[qRoot]){//低的指向高的parent[pRoot] = qRoot;//这里不需要维护qroot的优先级,因为这棵树的高度没有改变}else if(rank[pRoot] > rank[qRoot]){parent[qRoot] = pRoot;}else{//相等parent[pRoot] = qRoot;//维护qRoot的rankrank[qRoot] += 1;}}//实现方式一样public boolean isConnected(int p, int q) {return false;}}复制
路径压缩1:
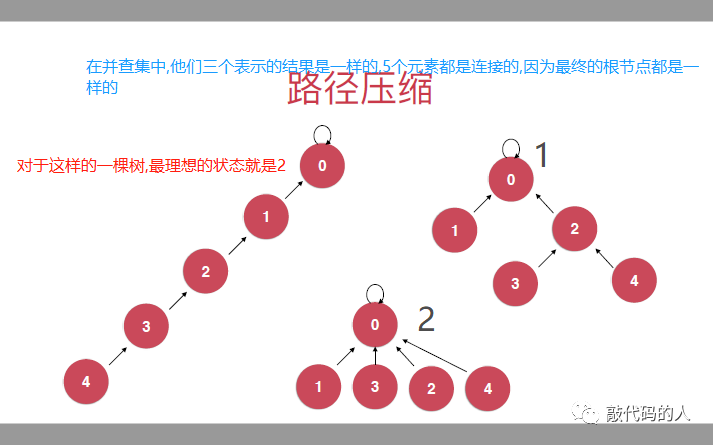
问题:对于基于rank的优化中,树的高度还是一直增加
方案解决:
在并查集中,只要最终的父亲节点一样,那么表示的这两个元素就是连接的
所以在每次寻找元素根节点这个过程中,我们可以把这个节点向父亲节点靠拢,来缩短树的高度
就是把这个节点直接指向他父亲的父亲
最终合并的时候还是安装高度优先级
对于压缩后并不需要维护rank,他表示的是优先级,不是高度
动态图简单演示
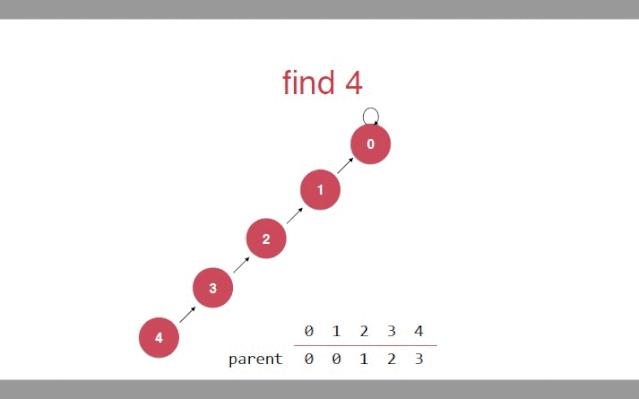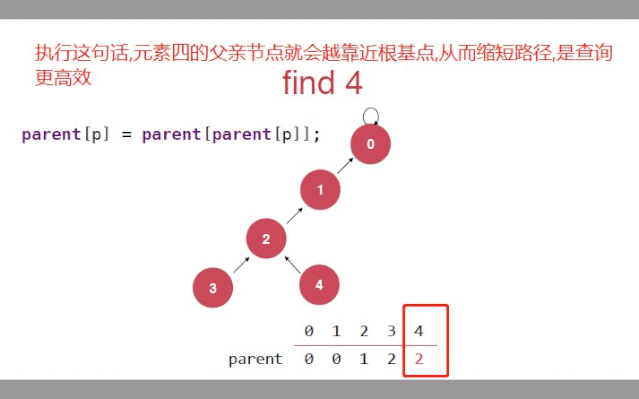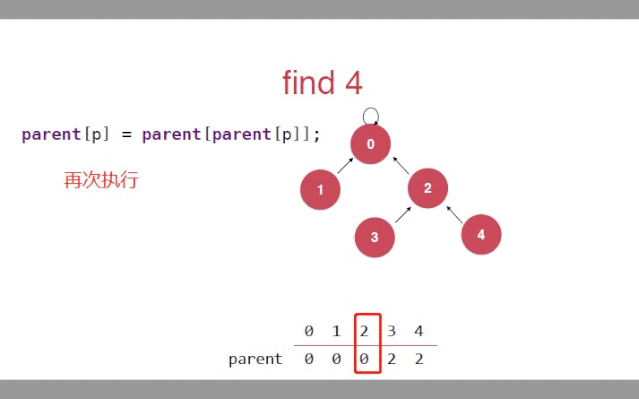
只要针对find()方法
//需要在find方法中,改变树的高度//对于给定的索引(节点)查找他的根节点public int find(int p){//判断索引的有效性if(p < 0 && p >= id.length){throw new IllegalArgumentException("p is out of bound");}//数组中对应索引的值(父亲节点),它又作为新的索引去寻找父亲//当索引和找到的父亲一样时,就是自己指向自己,就是根节点while(p != parent[p]){parent[p] = parent[parent[p]]//去指向爷爷p = parent[p];}return p;}复制
路径压缩加强版
查找时,把所有的节点都指向父亲节点
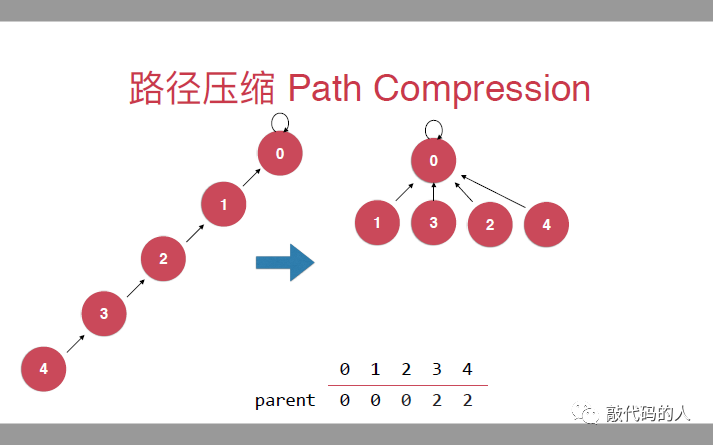
find方法实现
//需要在find方法中,改变树的高度//对于给定的索引(节点)查找他的根节点public int find(int p){//判断索引的有效性if(p < 0 && p >= id.length){throw new IllegalArgumentException("p is out of bound");}//数组中对应索引的值(父亲节点),它又作为新的索引去寻找父亲//当索引和找到的父亲一样时,就是自己指向自己,就是根节点while(p != parent[p]){//我们会把此节点上面所有的节点都去指向根节点,//所以根节点就是父亲节点//直接返回return parent[p];parent[p] = find(parent[p]);return parent[p];}return p;}复制
喜欢,转发
明天见







