
本文的起始,来自知乎的这个问题:
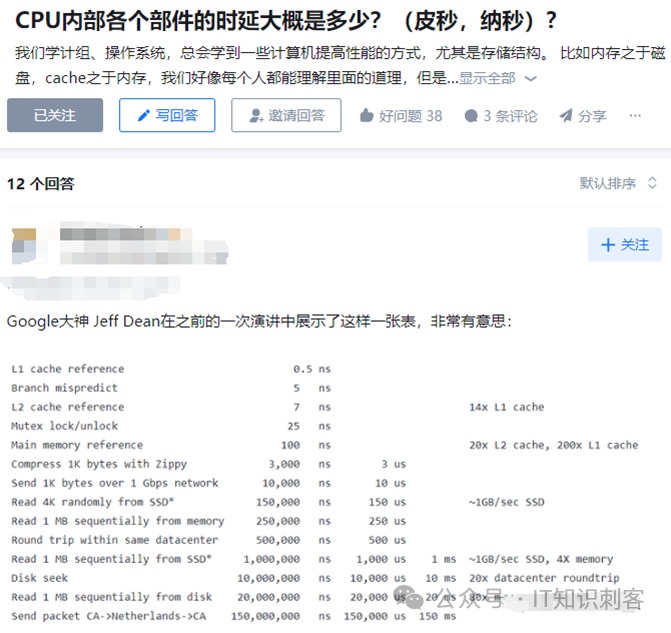
自己动手测量,其实是一个很好的研究过程。这个过程中,你可以学到很多东西,大大扩展自己的知识边界。这是只看一眼Jeff Dean的测量结果,学不到的。所以,本文当然不会结束。
add $1, %rax复制
CPU厂商仍在不断复杂化微架构,让IPC更高,比如,Intel有一个宏融合,将两条指令合成一条同时执行,这样理论上的IPC可以超过4。
但实际上别说4了,能达到1都不错了。因为对于指令级并行,有各种各样的限制,IPC为4只是理论上限,通常达不到。
比如,做一次最常见的主键索引等值扫描,Oracle程序的平均IPC可以达到1,已经是遥遥领先了。
MySQL、PG,在0.6, 0.7上下。
国产数据库,基于PG/MySQL封装的还好,有PG/MySQL为基础,不会太差。那种纯自研的,我不说了,你懂得。他们都不知道如何进行这种测量。
回到我们的问题,IPC如果为4的话,1亿次加法,是否需要2千5百万周期?
理论上是这样。但还要考虑1亿次加法的实现。
我们只能用一个循环,来完成1亿次加法,如:
While ( 1亿次循环 ){add $1, %rax}复制
那么,CPU实际执行的指令流如下:
add $1, %raxadd $1, %raxadd $1, %rax……1亿条add
这1亿条ADD,是互相依赖的。IPC为4,是同时执行4条无依赖的指令,这种有依赖的,第二条ADD要使用第一条ADD的结果,IPC只能为1,也就是吞吐量只能为1。一周期运行1条ADD。
我们绕了一圈,得到的结论就是,循环中的1亿条加法,需要1亿个周期。IPC为1。
为什么要绕这一圈,如果你还在认真阅读,马上就能知道了。
好了,总结一下,我们如下可以测量、并计算出CPU的频率:
1亿条加法总周期 / 1亿加法总时间 = 主频
我们可以得知,循环中的1亿条加法,需要1亿个周期。被除数已经知道了:1亿。
现在就差测量一下总时间,就能得到除数了。1亿条加法的总时间,也十分容易测量,完整的程序如下:
intwork(unsigned long *fg){structtimeval tv1, tv2;__u64 begin = 0, end = 0;register int i, k = 0;unsigned long num = (unsigned long) fg[0];gettimeofday(&tv1, 0);begin = rdtscp();for (i=0, k=0; i<num; i++){k = k + 1;}end = rdtscp();gettimeofday(&tv2, 0);printf("TSC: %u %i\n",(end-begin), k);printf("%d.%ld - %d.%ld = %ld\n",tv2.tv_sec, tv2.tv_usec, tv1.tv_sec, tv1.tv_usec, (tv2.tv_sec - tv1.tv_sec) * 1000 * 1000 + (tv2.tv_usec - tv1.tv_usec));return k;}复制
编译:
[root@oracledbff]# gcc -g measure2.c -o m2[root@oracledbff]#复制
运行:
[root@oracledb ff]# ./m2_1 0 100000000TSC: 100607598 1000000001704438157.506083 - 1704438157.458064 = 48019复制
48019,是程序总的微秒数,乘以1000,即为纳秒数,1亿除以48019000,即:100000000/(48019*1000.),得2.0825。
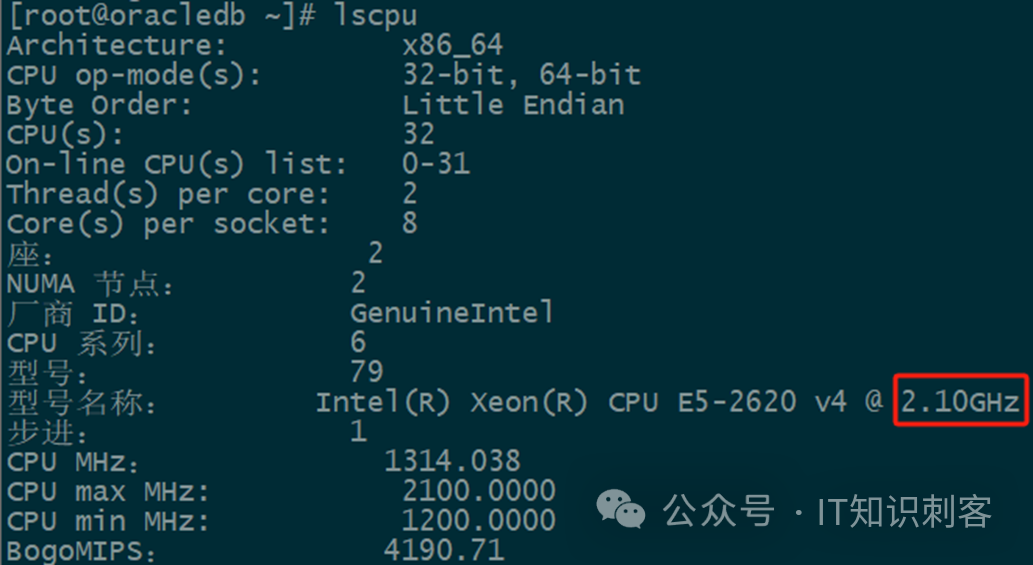
这是一台主频为2.1GHz的至强CPU: Intel(R) Xeon(R) CPU E5-2620 v4 @ 2.10GHz。
我们测量的结果,2.0825,和 lscpu 查看到的主频,基本一致。
有一点偏差,是gettimeofday等函数自身消耗导致的。
[root@oracledb ~]# cat /sys/devices/system/cpu/intel_pstate/min_perf_pct40[root@oracledb ~]# echo 100 > /sys/devices/system/cpu/intel_pstate/min_perf_pct[root@oracledb ~]#复制
A: 0x000000000040087a <+110>: add $0x1,%ebx // k = k + 1B: 0x000000000040087d <+113>: add $0x1,%r12d // i++,为了控制循环次数C: 0x0000000000400881 <+117>: movslq %r12d,%rax // 为了控制循环次数D: 0x0000000000400884 <+120>: cmp -0x28(%rbp),%rax // 为了控制循环次数E: 0x0000000000400888 <+124>: jb 0x40087a // 循环,向上跳转复制
但这里第二、三、四、五条指令相依赖。它们又怎能在一个周期内同时执行?
为了讲明白这个问题,我在指令前加了A、B、……、E这样的字母编号。其中,D和E会宏融合成一条指令,记为DE。实际执行的指令,是A、B、C、DE。
CPU实际执行的,是A B C DE A B C DE A B C DE A B C DE …… 这样的指令流。
这个指令流对应着我们的循环,是我们的循环生成的。我把指令流中第一次循环对应的指令记为A1,B1,C1,DE1。第二次循环对应指令记为A2,B2,C2,DE2。等等。
下面我们看看每个周期,CPU是如何执行指令流中的这些指令的。
第一周期,执行A1, B1。
C1,DE1,依赖A1、B1的结果,无法被执行。这一周期只有两条指令执行,C1、DE1处于等待状态。
第二周期,执行C1,DE1,同时还会执行A2,B2。
C1和DE1上一周期已经是等待状态了,这一周期当然可以执行。
因为Intel/AMD这种复杂指令集x64微架构 IPC 上限就是4(DE算一条指令),C1、DE1才两条指令,而且A2、B2也并不依赖C1、DE1的结果,因此这一周期中除了C1、DE1被执行外,还会执行A2、B2。这样IPC就已经达到4了。
第三周期,执行C2,DE2,A3,B3。
第四周期,执行C3,DE3,A4,B4。
……
你看,从第二周期开始,IPC就是4了(如果DE算两条指令的话,实际是5)。
虽然这4条指令中,有两条是上一次循环的,两条是本次循环的。但从宏观上看,循环的4条指令,可以在一周期内全部执行完成。
所以,这里不使用O2编译,指令多了一点,也没关系。
我们再强调下,对于CPU来说,没有循环、没有分枝条件,就是指令流。A1 B1 C1 DE1 A2 B2 C2 DE2 A3 B3 ……,A1亿 B1亿 C1亿 DE1亿。
CPU在指令流中,选择无依赖的、可以同时执行的指令去执行。一次最多选4个指令。
第一次(也就是第一个周期):
A1 B1 C1 DE1 A2 B2 C2 DE2 A3 B3 ……,A1亿 B1亿 C1亿 DE1亿。
只能选中A1、B1,后面的指令都要等待A1、B1的结果。
第二次(第二周期):
A1 B1 C1 DE1 A2 B2 C2 DE2 A3 B3 ……,A1亿 B1亿 C1亿 DE1亿。
选择C1 DE1 A2 B2,这4条指令无依赖,可以同时执行。虽然它们分属不同次循环,但并不影响它们被一起执行。别忘了,前面说过,CPU眼中并没有循环,就是指令流。
(免骂声明:严谨的说法是CPU中执行单元眼中,并没有循环,就是指令流。)
(估计你能看到这儿,面对这些不严谨的小细节也不会开骂了。)
测量,不是关键。CPU的主频lscpu就能得到,我们测量的结果还有少量误差。通过测量,你能把平生所学,串联、运用起来,可以扩展你的知识边界。掌握原理是关键,测量只是学习原理的方法。
讲述深入研究、学习的方法,是本文、甚至这个系列的目的。因为能深入了解底层的人材,在现在的基础软件开发领域(起码在我所在的数据库领域),实在是太缺了。
可不要认为频率测量没有用,搞明白了频率测量,把这些知识点串起来,你自然就懂得了程序优化。
坐稳了,我们要深一步了。
测量当然不是我们的最终目的,最终目的是如何写出能榨干CPU每一个周期的、能效最高的程序。做到了这一点,才是真正的HPC编程,才是基础软件开发,应有的样子。(要不然开发的可以叫平台软件,称不上基础软件)
为了最高的能效,我再提个问题:如果我真的要进行1亿次加法,如何才能更快的完成?
好了,本篇就到这里,给你点时间消化消化,下一篇,马上发布,关注IT知识刺客,不错过精彩内容。










