skiplist(跳表)的应用场景
1. 几种常用的数据结构
在学习跳表之前,我们先来比较下数组、链表、二叉查找树、平衡二叉树的一些比较:
数组:支持随机访问,在有序情况下可以采用二分查找(binarySearch)来快速查找。缺点也很明显:在有序数组中插入和删除数据时,为了保持元素的有序性,需要进行大量的数据移动操作。
链表:维护前后节点的指针,有序情况下,插入和删除数据操作比较简单。缺点就是没有办法快速查找,二分查找并不适用。
二叉查找树:支持高效的二分查找,也能快速地进行插入和删除操作。缺点是在某些极端情况下,二叉查找树可能变成一个线性链表。
平衡二叉树:对二叉树的缺点进行了改进,引进了平衡的概念。根据平衡算法的不同,具体实现有AVL树/B树(B-Tree)/B+树(B+Tree)/红黑树等。但是平衡二叉树实现起来比较复杂,较难理解。
2. 跳表
1. 结构
跳表由William Pugh 1989年发明。他在论文《Skip lists: a probabilistic alternative to balanced trees》中详细介绍了跳表的数据结构和插入删除等操作。论文是这么介绍跳表的:
Skip lists are a data structure that can be used in place of balanced trees.
Skip lists use probabilistic balancing rather than strictly enforced balancing and as a result the algorithms for insertion and deletion in skip lists are much simpler and significantly faster than equivalent algorithms for balanced trees.复制
引用自:https://en.wikipedia.org/wiki/Skip_list
跳表是一个“概率型”的数据结构,在很多应用场景中可以替代平衡树。与平衡树相比,有相似的渐进期望时间边界,但是它更快,更简单也更省空间。
是一个分层结构的多级链表,最下层链表包括所有数据,每个层级都是下一层级的索引,是一个用空间换时间的方案:
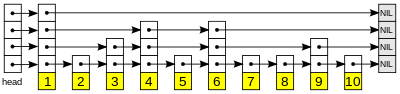
2. 复杂度
红黑树:插入、查找为O(logn),但常数项较小;无锁实现的复杂性很高,一般需要加锁;数据天然有序。
SkipList:插入、查找为O(logn),但常数项比红黑树要大;底层结构为链表,可无锁实现;数据天然有序。
skiplist性能:
| 场景 | 平均值 | 最坏情况 |
|---|---|---|
| 查找 | O(logn) | O(n) |
| 插入 | O(logn) | O(n) |
| 删除 | O(logn) | O(n) |
目前redis的zset和levelDB存储结构采用的就是skiplist。
3. 跳表特性
一个普通的有序链表:

如果从上面的列表中查找23需要遍历4次,查找59时需要遍历6次。而对这个链表,我们没法使用二分查找。
于是我们对数据节点加上一级索引如下图:
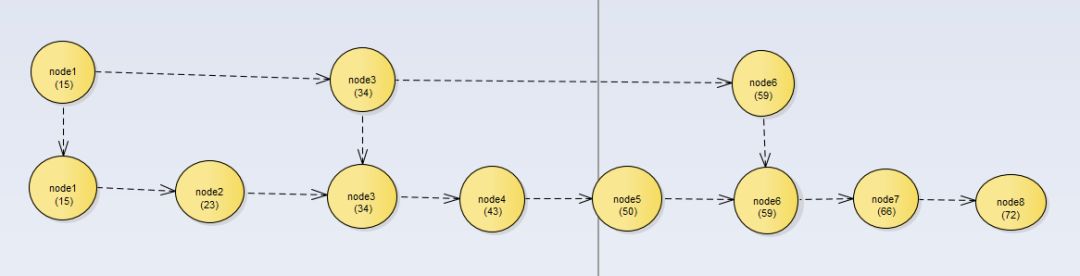
这样通过一级索引去找就相对来说快上很多。
还可以加上二级索引,如下图:
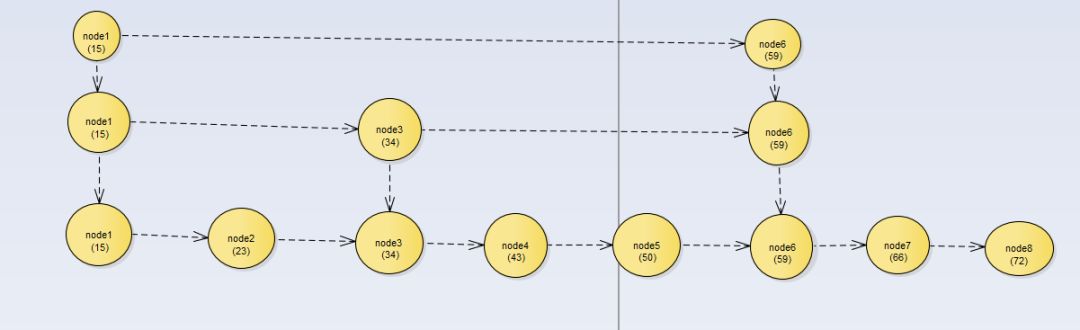
跳表结构:
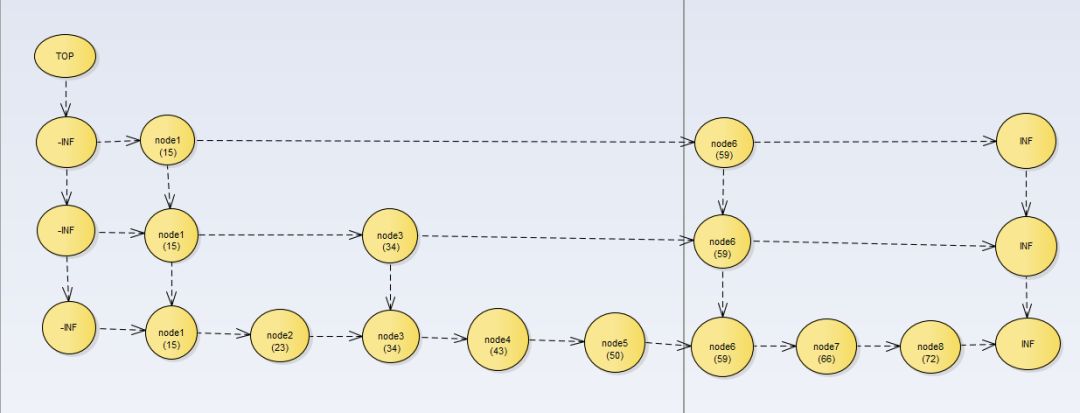
跳跃表的层数,我们称之为维度,从上到下,我们称之为降维,它由很多个维度维成。
每一层都是一个有序的链表。
每一层中相同的元素,我们称为“同位素”。
Skip List主要思想是将链表与二分查找相结合,它维护了一个多层级的链表结构(用空间换取时间),可以把Skip List看作一个含有多个行的链表集合,每一行就是一条链表,这样的一行链表被称为一层,每一层都是下一层的"快速通道",即如果x层和y层都含有元素a,那么x层的a会与y层的a相互连接(垂直)。最底层的链表是含有所有节点的普通序列,而越接近顶层的链表,含有的节点则越少。
最底层的链表,即包含了所有元素节点的链表是L1层,或称基础层。除此以外的所有链表层都称为跳跃层。
基础层包括所有的元素。
对一个目标元素的搜索会从顶层链表的头部元素开始,然后遍历该链表,直到找到元素大于或等于目标元素的节点,如果当前元素正好等于目标,那么就直接返回它。如果当前元素小于目标元素,那么就垂直下降到下一层继续搜索,如果当前元素大于目标或到达链表尾部,则移动到前一个节点的位置,然后垂直下降到下一层。
Skip List还有一个明显的特征,即它是一个不准确的概率性结构,这是因为Skip List在决定是否将节点冗余复制到上一层的时候(而在到达或超过顶层时,需要构建新的顶层)依赖于一个概率函数,举个栗子,我们使用一个最简单的概率函数:丢硬币,即概率P为0.5,那么依赖于该概率函数实现的Skip List会不断地"丢硬币",如果硬币为正面就将节点复制到上一层,直到硬币为反。
相比于二叉查找树,跳表维持结构平衡的成本比较低,完全靠随机。而二叉查找树需要Rebalance来重新调整平衡的结构。
删除时自上而下,查找第一次出现节点的索引,并逐层找到每一层对应的节点,删除每一层查找到的节点,如果该层只剩下1个节点,删除整个一层(原链表除外)。
4. java实现
存储结构一般为:
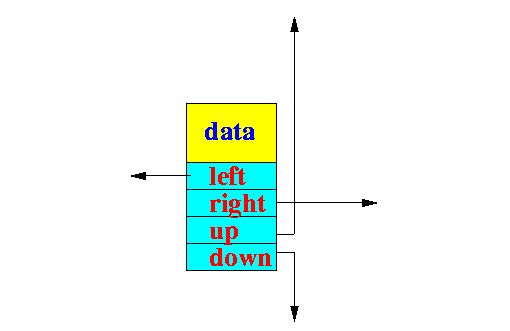
jdk中提供的实现主要有:ConcurrentSkipListMap与ConcurrentSkipListSet,其中后者是基于前者实现的。关于这两个的源码分析,请关注之后的文章。
5. 参考
https://en.wikipedia.org/wiki/Skip_list






