抽样分布之χ2 分布，t分布，F分布

文章目录

• 文章目录

• 1. 分布

• 2. 分布

• 3. 分布

1. 分布

• 定义

  设 是来自总体的样本，则称统计量

  服从自由度为的分布，记为

  
  

  ❝

  此处的自由度是指独立变量的个数

  ❞

• 分布的概率密度

  其图像如下

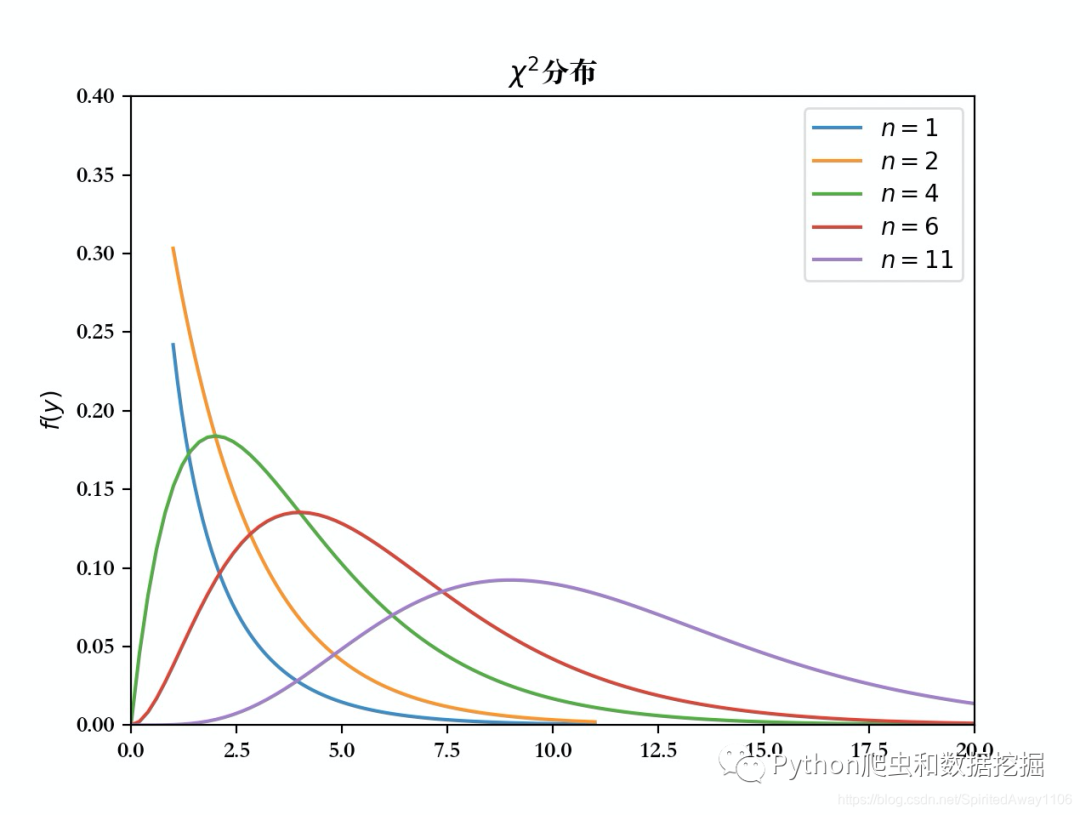
• 图像为单峰曲线
• 图像为非对称图形
• 时，在处取得最大值
• 越大，峰越往右，图像也越趋于对称，当很大时，可近似看做正态分布

• 分布性质

1. 分布的可加性

   设，并且相互独立，则有

   
   

2. 分的数学期望和方差

   证明：

   ❝

   由于 ，其中  ,因此有

   因此

   我们需要知道， 目前没有更好的方式，我们尝试使用期望的定义进行计算

   这里对后面的积分项可继续采用分部积分方法进行处理，但是这地方其实有个技巧 ，根据期望定义有

   前面我们已经算出

   因此有

   所以有

   ❞

• 分布的分位点

  对于给定的正数，称满足条件

  的点 为分布的上分位点

  
  

• 补充函数介绍




• 性质1

   

  推论1 
  推论2 
  推论3   

• 性质2

  对于

• 补充 分布介绍

  分布是统计学的一种连续概率函数，是概率统计中一种非常重要的分布。指数分布和χ2分布都是伽马分布的特例

• 假设随机变量为等到第件事发生所需的等候时间, 密度函数为

  其中参数为形状参数， 为逆尺度参数

• 分布具有可加性

• 当形状参数α=1时，伽马分布就是参数为的指数分布，即

• 当时，伽马分布就是自由度为的卡方分布，即

2. 分布

• 定义

  设，且相互独立，则称随机变量

  服从自由度为的「分布」 . 记为

  
  

• 分布概率密度

  其图像如下

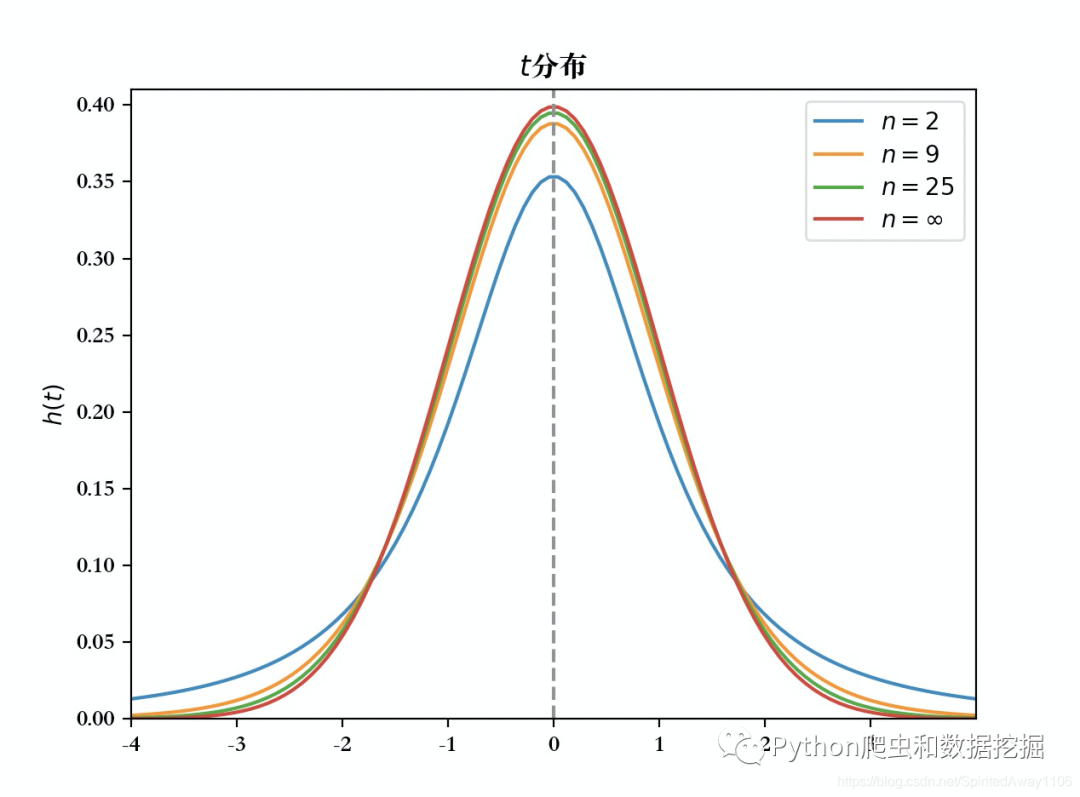
• 以0为中心，左右对称的单峰分布；

• 越小，曲线越低平；越大，t分布曲线越接近标准正态分布曲线

• 当时，分布近似于标准正态分布

• 分布的分位点

  对于给定的正数，称满足条件

  的点 为分布的上分位点

  
  

• 由图像的对称性可知

3. 分布

• 设，且相互独立，则称随机变量

  服从自由度为的分布，记为

  
  

• 分布概率密度

  其图像为

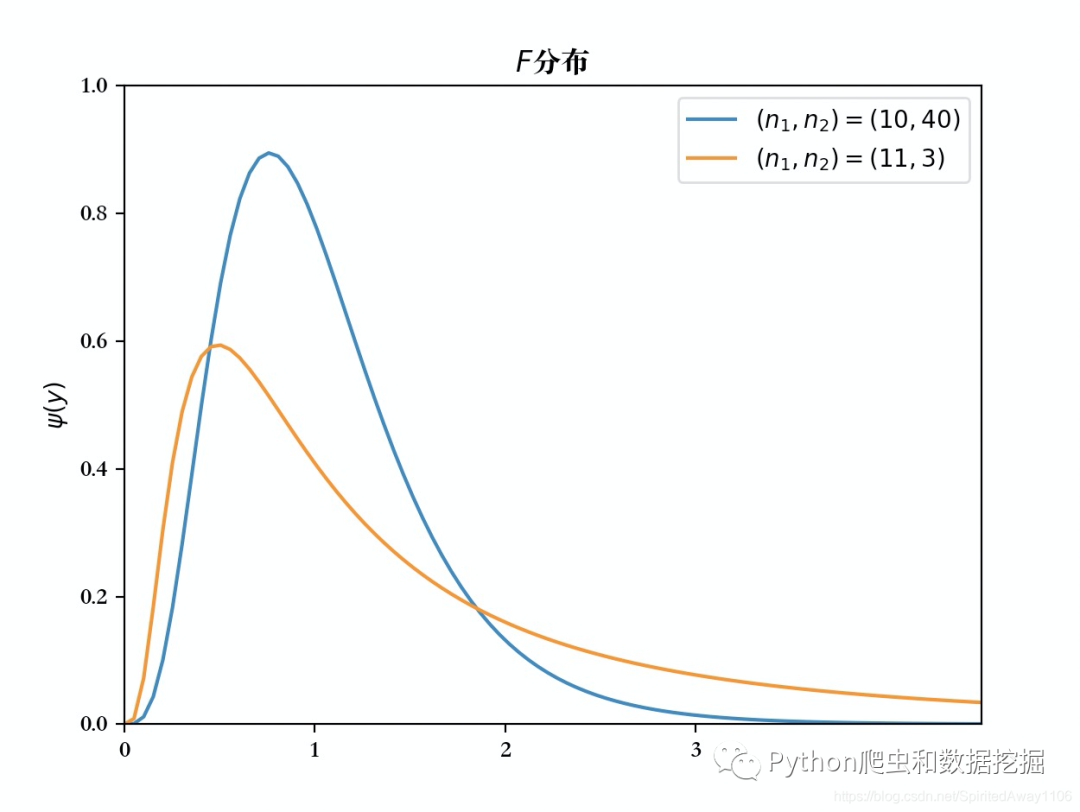
• 由定义可知，若，则

  
  

• 分布的分位点

  对于给定的正数，称满足条件

  的点 为分布的上分位点.

  
  

• 分位点性质

  证明如下

  ❝

  根据分布分位点的定义可知

  ❞