HyperCalm Sketch-One-Pass Mining Periodic Batches in Data Streams.pdf

章芋文

102

13页

3次

2023-08-29

免费下载

HyperCalm Sketch: One-Pass Mining Periodic

Batches in Data Streams

Zirui Liu

†

, Chaozhe Kong

†

, Kaicheng Yang

†

, Tong Yang

†‡

, Ruijie Miao

†

Qizhi Chen

†

, Yikai Zhao

†

, Yaofeng Tu

, and Bin Cui

†

School of Computer Science, and National Engineering Laboratory for Big Data Analysis Technology and Application,

Peking University, Beijing, China

‡

Peng Cheng Laboratory, Shenzhen, China

ZTE Corporation

{zirui.liu, kcz, ykc, miaoruijie, hzyoi, zyk, bin.cui}@pku.edu.cn, {yangtongemail}@gmail.com, {tu.yaofeng}@zte.com.cn

Abstract—Batch is an important pattern in data streams, which

refers to a group of identical items that arrive closely. We ﬁnd

that some special batches that arrive periodically are of great

value. In this paper, we formally deﬁne a new pattern, namely

periodic batches. A group of periodic batches refers to several

batches of the same item, where these batches arrive periodically.

Studying periodic batches is important in many applications, such

as caches, ﬁnancial markets, online advertisements, networks,

etc. We propose a one-pass sketching algorithm, namely the

HyperCalm sketch, which takes two phases to detect periodic

batches in real time. In phase 1, we propose a time-aware

Bloom ﬁlter, namely HyperBloomFilter (HyperBF), to detect the

start of batches. In phase 2, we propose an enhanced top-k

algorithm, called Calm Space-Saving (CalmSS), to report top-

k periodic batches. We theoretically derive the error bounds for

HyperBF and CalmSS. Extensive experiments show HyperCalm

outperforms the strawman solutions 4× in term of average

relative error and 13.2× in term of speed. We also apply

HyperCalm to a cache system and integrate HyperCalm into

Apache Flink. All related codes are open-sourced.

Index Terms—Data Stream, Sketch, Periodic Batch

I. INTRODUCTION

A. Background and Motivation

Batch is an important pattern in data streams [1], which is

a group of identical items that arrive closely. Two adjacent

batches of the same item are spaced by a minimum interval

T , where T is a predeﬁned threshold. Although batches can

make a difference in various applications, such as cache [1],

networks [2], and machine learning [3], [4], it is not enough

to just study batches. For instance, in cache systems, with

just the measurement results of batches, we are still not able

to devise any prefetching method and replacement policy.

Further mining some special patterns of batches is of great

importance. On the basis of batches, we propose a new pattern,

namely periodic batch. A group of periodic batches refers to

α consecutive batches of the same item, where these batches

arrive periodically. We call α the periodicity. Finding top-

k periodic batches refers to reporting k groups of periodic

batches with the k largest periodicities.

Studying top-k periodic batches is important in practice. For

example, consider a cache stream formed by many memory

access requests where each request is an item, periodic batches

provide insights to improve the cache hit rate. With the

Co-primary authors: Zirui Liu, Chaozhe Kong, and Kaicheng Yang. Corre-

sponding author: Tong Yang (yangtongemail@gmail.com).

historical information of periodic batches, we can forecast

the arrival time of new batches, and prefetch the item into

cache just before its arrival. For another example, in ﬁnancial

transaction streams, periodic transaction batches could be an

indicator of illegal market manipulation [5]. By detecting

periodic batches in real time, we can quickly ﬁnd those

suspicious clients that might be laundering money. Periodic

batches are also helpful in recommendation systems and

online advertisements, where the data stream is generated

when users click or purchase different commodities. A batch

forms when users continuously click or purchase the same

type of commodities. In this scenario, periodic batches imply

users’ seasonal and periodic browsing or buying behaviors [6]

(e.g., Christmas buying patterns that repeat yearly, or seasonal

promotion-related user behaviors). Studying periodic batches

can help us to better understand customer behavior, so that we

can deliver appropriate advertisements promptly to customers.

In addition, periodic batches are also important in networks.

In network stream, most TCP senders tend to send packets

in periodic batches [7]. If we can forecast the arrival time

of future batches, we can pre-allocate resources to them, or

devise better strategies for load balancing. To our knowledge,

there is no existing work studying periodic batches, and we

are the ﬁrst to formulate and address this problem.

Finding periodic batches is a challenging issue. First, ﬁnding

batches is already a challenging issue. Until now, the state-of-

the-art solution to detect batches is Clock-Sketch [1], which

records the last arrival time of recent items in a cyclic array,

and uses another thread to clean the outdated information using

CLOCK [8] algorithm. However, to achieve high accuracy, it

needs to scan the cyclic array very fast, which consumes a

lot of CPU resources. Second, periodic batch is a more ﬁne-

grained deﬁnition, and thus ﬁnding periodic batches is more

challenging than just ﬁnding batches. The goal of this paper

is to design a compact sketch algorithm that can accurately

ﬁnd periodic batches with small space- and time- overhead.

B. Our Proposed Solution

To accurately detect periodic batches in real time, we

propose a one-pass sketching algorithm, namely HyperCalm.

HyperCalm takes two phases to ﬁnd top-k periodic batches. In

phase 1, for each item e arriving at time t, we check whether

it is the start of a batch. If so, we query a TimeRecorder

2023 IEEE 39th International Conference on Data Engineering (ICDE)

DOI 10.1109/ICDE55515.2023.00009

Authorized licensed use limited to: ZTE CORPORATION. Downloaded on August 29,2023 at 02:09:27 UTC from IEEE Xplore. Restrictions apply.

queue to get the arrival time

t of the last batch of e, and

calculate the batch interval V = t −

t. Then we send

this batch and its interval e, V  to the second phase. In

phase 2, we check periodicity and manage to record top-

k periodic batches, i.e., top-k e, V  pairs. In phase 1, we

devise a better algorithm than the state-of-the-art algorithm for

detecting batches, Clock-Sketch [1]. In phase 2, we propose an

enhanced top-k algorithm, which naturally suits our periodic

batch detection scenario.

In phase 1, we propose a time-aware version of Bloom

ﬁlter, namely HyperBloomFilter (HyperBF for short), to detect

batches. For each incoming item, phase 1 should report

whether the item is the start of a batch. In other words, this

is an existence detection algorithm. In addition to existence

detection, phase 1 should be aware of arrival time to divide

a series of the same item into many batches. Bloom ﬁlter [9]

is the most well-known memory-efﬁcient data structure used

for existence detection. However, the existence detection of

Bloom ﬁlter is only low-dimensional, i.e., it is agnostic to time

dimension. Typical work aware of time dimension is Persistent

Bloom ﬁlter (PBF) [10]. It is an elegant variant of Bloom

ﬁlter, which uses a set of carefully constructed Bloom ﬁlters

to support membership testing for temporal queries (MTTQ)

(e.g., has a person visited a website between 8:30pm and

8:40pm?). MTTQ and batch detection are different ways to

be aware of time dimension. To enable Bloom ﬁlter to be

aware of time, our HyperBF extends each bit in Bloom ﬁlter

into a 2-bit cell, doubling the memory usage. Compared to

the standard Bloom ﬁlter, HyperBF has the same number of

hash computations and memory accesses for each insertion

and query. The only overhead for time awareness is doubling

the memory usage, which is reasonable and acceptable.

In phase 2, we propose an enhanced top-k algorithm,

called Calm Space-Saving (CalmSS for short), to report top-k

periodic batches. For each incoming batch and its interval, i.e.,

e, V , phase 2 should keep periodic batches with large peri-

odicities, and evict periodic batches with small periodicities.

In other words, phase 2 keeps frequent e, V  pairs, and evicts

infrequent e, V  pairs, which is is a top-k algorithm. Typical

top-k algorithms include Space-Saving [11], Unbiased Space-

Saving [12], and Frequent [13]. However, their accuracy is

signiﬁcantly harmed by cold items

. This problem is more

serious in our scenario of periodic batch detection. This is

because one infrequent item may have multiple batches, and

one frequent item may also have multiple batches without

periodicity. Both the two cases above increase the number of

cold e, V  pairs. To identify and discard cold items, Cold

Filter [16] and LogLogFilter [17] record the frequencies of all

items in a compact data structure. However, considering the

large volume of data stream, this structure will be ﬁlled up very

quickly, and needs to be cleaned up periodically. To ensure the

one-pass property of our solution, it is highly desired to devise

a data structure which will never be ﬁlled up. Instead of record-

Cold items refer to items with small frequencies (i.e., infrequent items),

and hot items refer to items with large frequencies (i.e., frequent items). In

practice, most items are cold items, which appear just several times [14], [15]

ing all items, our solution is to just record the frequencies

of some items in the sliding window, and discard those cold

items in the sliding window. Rather than using existing sliding

window algorithms [18], [19], [20], this paper designs an LRU

queue working together with Space-Saving because of the

following reasons. First, our LRU queue is elastic: users can

dynamically tune its memory usage to maintain a satisfactory

accuracy. Second, our LRU queue has elegant theoretical

guarantees (see details in § III-C). Third, our LRU queue can

be naturally integrated into the data structure of Space-Saving

(see details in § III-D): such combination achieves higher

accuracy and higher speed. Our combination is faster because

the LRU queue efﬁciently ﬁlters most cold items, and thus

the complicated replacement operations incurred by cold items

are avoided (see Figure 11c). Actually, besides the application

of periodic batch detection, our LRU queue can improve the

accuracy/speed of any streaming algorithms. We can handle

any case that Cold ﬁlter can handle, and we are both time-

and space- more efﬁcient than Cold ﬁlter (§ V-C). All related

codes are open-sourced [21].

C. Key Contributions

• We formulate the problem of ﬁnding periodic batches in

data streams. We believe this is an important problem in

data mining.

• We propose an accurate, fast, and memory efﬁcient Hyper-

Calm sketch to detect periodic batches in real time. Both

the two components of HyperCalm, HyperBF and CalmSS,

signiﬁcantly outperform the state-of-the-art solutions in de-

tecting batches and ﬁnding top-k items, respectively.

• We derive theoretical guarantees for our HyperBF and

CalmSS, and validate our theories using experiments.

• We conduct extensive experiments showing that HyperCalm

well achieves our design goal. The results show HyperCalm

outperforms the strawman solutions 4× in term of average

relative error and 13.2× in term of processing speed.

• We apply HyperCalm to a cache system showing that peri-

odic batches can beneﬁt real-world application. We integrate

HyperCalm into Apache Flink [22] showing that HyperCalm

can smoothly work in distributed systems.

II. B

ACKGROUND AND RELATED WORK

A. Problem Statement

Batches: A data stream is an inﬁnite sequence of items where

each item is associated with a timestamp. A batch is deﬁned

as a group of identical items in the data stream, where the

time gap between two adjacent batches of the same item must

exceed a predeﬁned threshold T . For convenience, in this

paper, two adjacent batches mean two batches belong to the

same item by default. The arrival time of a batch is deﬁned

as the timestamp of the ﬁrst item of this batch. We deﬁne the

interval/time gap between two adjacent batches as the interval

between their arrival times.

Periodic batches: A group of periodic batches refers to α

consecutive batches of the same item, where these batches

arrive with a ﬁxed time interval. We call α the periodicity.

Authorized licensed use limited to: ZTE CORPORATION. Downloaded on August 29,2023 at 02:09:27 UTC from IEEE Xplore. Restrictions apply.

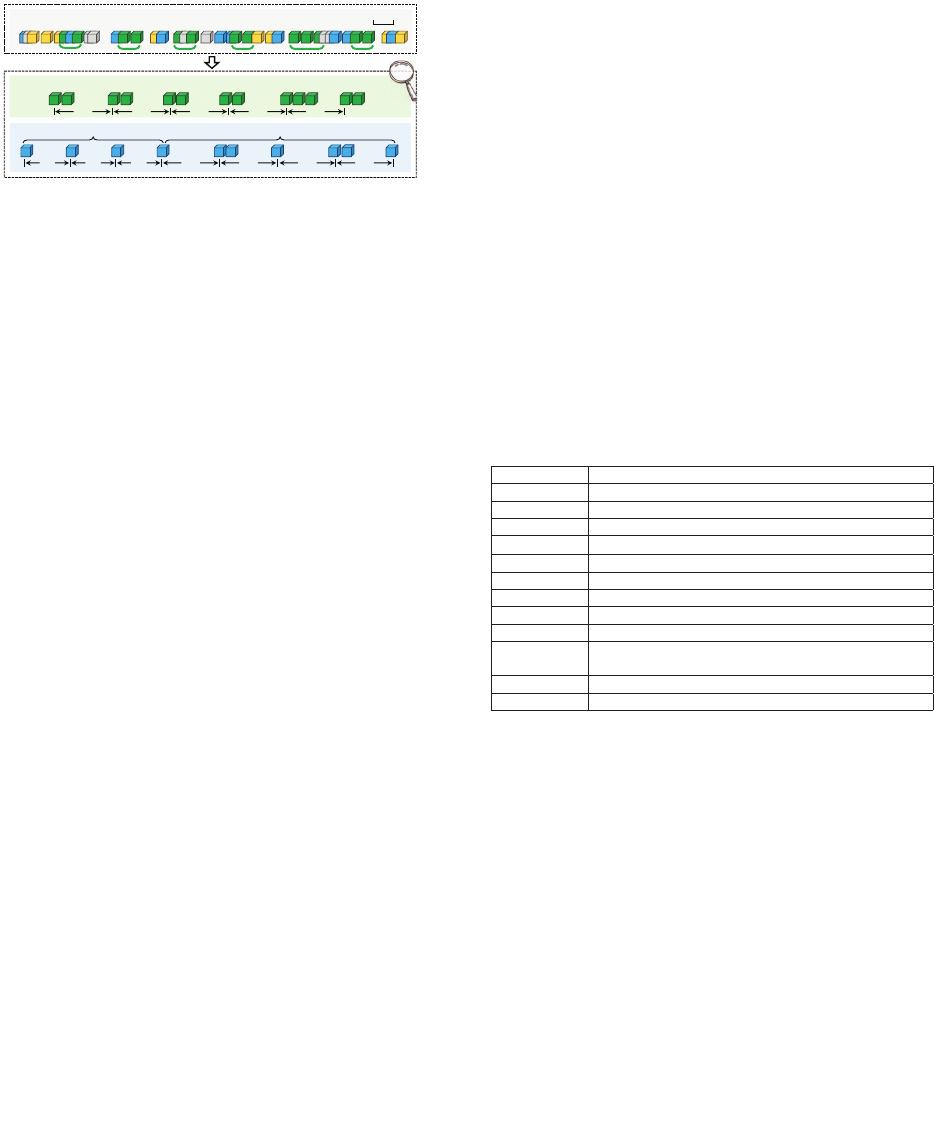
Here, the “ﬁxed time interval” is not the exact time, but the ap-

proximate (noise-tolerant) time rounded up to the nearest time

unit (e.g., one millisecond). Finding top-k periodic batches

refers to reporting k groups of periodic batches with the k

largest periodicities. Note that one item may have more than

one group of periodic batches, and thus can be reported more

than once.

Example (Figure 1): We present an example to further clarify

our problem deﬁnition. We focus on two kinds of distinct items

and e

in the data stream. For e

, its 6 batches form a

group of periodic batches. For e

, it has two groups of periodic

batches, with the periodicities of 4 and 5, respectively. Note

that some batches of e

just have one item.



    







  







   







Fig. 1: Example of periodic batches.

Discussion: The deﬁnition of periodic batches is a design

choice related to ﬁnal application. We think our deﬁnition of

periodic batches is most general, which can beneﬁt many real-

world applications (see § V-E as an example). However, certain

application may also care about other aspects of periodic

batches, such as batch size and distance. For example, some

application may just want to detect those periodic batches

that are large enough in size. It is not hard to detect those

variants of periodic batches by adding small modiﬁcation

to our solution. Further formulating more application-speciﬁc

variants of periodic batches is our future work.

B. Related Work

Related work is divided into three parts: 1) algorithms for

batch detection; 2) algorithms for ﬁnding top-k frequent items;

and 3) algorithms for mining periodic patterns.

Batch detection: Item batch is deﬁned very recently in [1],

which proposes Clock-Sketch to ﬁnd batches. Clock-Sketch

consists of an array of s-bits cells. For each incoming item,

it sets the d hashed cells as 2

− 1. For query, if one of the

d hashed cells is zero, it reports a batch. Clock-Sketch uses

an extra thread to cyclically sweep the cell array at a constant

speed and decreases the swept non-zero cells by one. The

sweeping speed is carefully selected to avoid false-positive

errors. Besides Clock-Sketch, some sliding window algorithms

can be applied to ﬁnd batches, including Time-Out Bloom

Filter (TOBF) [23] and SWAMP [24].

Finding top-k frequent items: To ﬁnd top-k frequent items

in data streams, existing approaches maintain a synopsis data

structure. There are two kinds of synopses: sketches and KV

tables. 1) Sketches usually consist of multiple arrays, each

of which consists of multiple counters. These counters are

used to record the frequencies of the inserted items. Typical

sketches include CM [25], CU [26], Count [27], and more

[28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38].

However, sketches are memory inefﬁcient because they record

the frequencies of all items, which is actually unnecessary. 2)

KV tables record only the frequent items. Typical KV table

based approaches include Space-Saving [11], Unbiased Space-

Saving [12], Frequent [13], and more [39], [40]. Space-Saving

and Unbiased Space-Saving record the approximate top-k

items in a data structure called Stream-Summary. However,

their accuracy is signiﬁcantly degraded by cold items. To

address this issue, Cold Filter [16] uses a two-layer CU sketch

to ﬁlter cold items. However, as aforementioned, the structure

of Cold Filter will be ﬁlled up very quickly. Cleaning the

full Cold Filter will inevitably incur error and time overhead,

which is still not addressed.

Mining periodic patterns: Although there have been some

algorithms aiming at mining periodicity in time sequence

data [41], [42], [43], [44], [45], [46], [47], their problem

deﬁnitions are different from ours. More importantly, most

of them do not meet the requirements of data stream model

processing: 1) each item can only be processed once; 2) the

processing time of each item should be O(1) complexity and

fast enough to catch up with the high speed of data streams.

For example, TiCom [44] deﬁnes a periodical problem in an

incomplete sequence data, and develops an iterative algorithm

with time complexity of O(n

). RobustPeriod [42] proposes

an algorithm based on discrete wavelet transform with time

complexity of O(n log n). Further, there are some works

which elegantly use Fast Fourier Transform (FFT) or Auto

Correlation Function (ACF) to address different deﬁnitions of

periodic items, such as SAZED [45]. These algorithms need

to process one item multiple times, and thus cannot meet the

above two requirements.

TABLE I: Symbols frequently used in this paper.

Symbol Meaning

e ID of an item in a data stream

T Batch threshold spacing two adjacent batches

d Number of arrays in HyperBF

The i

array of HyperBF

m Number of 2-bit cells in each array B

l Number of 2-bit cells in each block

(·) Hash function mapping an item into a cell in B

V Time interval of two adjacent batches of an item

c Length of the TimeRecorder queue

E = e, V 

An entry in phase 2, which is the concatenation of

an item e and its batch interval V , i.e., e, V 

w Length of the LRU queue in CalmSS

P Predeﬁned promotion threshold of the LRU queue

III. THE HYPERCALM SKETCH

Overview (Figure 2): The workﬂow of the HyperCalm sketch

consists of two phases: 1) A HyperBloomFilter (HyperBF)

detecting the start of batches; and 2) A Calm Space-Saving

(CalmSS) recording and reporting top-k periodic batches. In

addition, we design a TimeRecorder queue to record the last

batch arrival time for potential periodic batches. Given an

incoming item e arriving at time t, we ﬁrst propose HyperBF

to check whether it is the start of a batch. If so, we query the

Authorized licensed use limited to: ZTE CORPORATION. Downloaded on August 29,2023 at 02:09:27 UTC from IEEE Xplore. Restrictions apply.

of 13

免费下载

相关文档

评论