Calculation-of-Tight-Bounding-Volumes-for-Cyclic-CSG-Graphs.pdf

小小亮

601

10页

0次

2022-07-04

免费下载

Calculation of Tight Bounding Volumes for Cyclic CSG-

Graphs

Christoph Traxler Michael Gervautz

Institute of Computer Graphics

Technical University of Vienna

Karlsplatz 13/186-2

1040 WIEN

AUSTRIA

email: traxler@cg.tuwien.ac.at gervautz@cg.tuwien.ac.at

Abstract

Cyclic CSG graphs are a memory safe representation of objects with a very complex, recursive

structure. This class of objects are defined by CSG-PL-Systems, an adaption of the well known

Parametric Lindenmayer Systems (PL-Systems) to the CSG concept. They are a powerful tool to

model natural phenomena like plants, clouds or fractal terrain but also linear fractals or any objects

with a repetitive structure. CSG-PL-Systems are directly translated into CSG graphs, which are a

proper object representation for ray tracing. A derivation and geometric interpretation of strings is

no longer necessary. Because CSG graphs are as compact as the CSG-PL-Systems the memory

usage is low, so that restrictions of the complexit y of the scene are avoided. To be effici ent as well

it is very important to adapt conventional optimization techniques to CSG graphs. For CSG trees a

hierarchy of bounding volumes is buildt up by a simple recursive algorithm. A straight forward

transition of this algorithm to CSG graphs yields to very huge and thus useless bounding volumes.

In this paper we introduce an algorithm which calculates tight bounding volumes for the nodes of

cyclic CSG graphs. This method can also be applied to CSG trees with explicit transformation

nodes or CSG dags.

Key Words: CSG Graphs, Bounding Volumes, Ray Tracing

This project is supported by the “F ond zur Förderung der wissenschaftliche n Forschung (FWF)”, Austri a,

(project number: P09818)

1 Introduction

Cyclic CSG graphs are a memory safe representation of recursive objects, which are defined by

parallel rewriting systems. They are an extention to conventional CSG trees and thus can directly be

used for ray tracing. CSG graphs emerge from CSG-PL-Systems, which are an adaption of the well

known Parametric Lindenmayer-Systems (briefly PL-Systems). The main difference between PL-

Systems, which are fully described in [LIND90], and CSG-PL-Systems are their formal languages.

While the derived strings of the first are command sequences for a virtual construction tool called

turtle, the derived strings of the last are a subset of the infinite set of all valid CSG expressions.

Instead of running a derivation process and building up a large CSG tree out of the resulting string,

the rules of the grammar are directly transformed into a cyclic CSG-graph, which is traversed by the

rays to visualize the object.

For that purpose, we extended the CSG concept to three new nodes. Selection nodes, briefly S-

nodes, join all the rules for one grammar symbol and are associated with a selection function. This

function controls the flow by selecting a proper rule and passing the rays to it. The rules themselves

are translated into CSG trees and attached as successors to the S-Node. For each occurrence of a

grammar symbol in the right hand side of a rule an edge is spanned to the corresponding S-node.

This yields to a graph with cycles, wherby S-nodes are the only targets of cyclic edges.

Like with conventional CSG trees, the rays are mapped from the world coordinate frame into the

object coordinate frame, because this is much more efficient than mapping the primitive objects. In

CSG graphs this is done by special nodes, called Transformation nodes or briefly T-nodes. They can

be seen as unary operators and thus have only one successor. The same is true for Calculation

nodes, briefly C-nodes, which evaluate a finite set of arithmetic expressions to modify global

parameters. Their values effect flow control, i.e. the selection of rules, and transformations. All

other nodes, i.e. CSG operators and primitive objects are handled as in CSG trees. The CSG graphs

introduced so far are as compact as the describing data set. An explicit representation of the scene

(like with CSG trees) is avoided and therefore no restrictions of the complexity of the scene or the

approximation accuracy of objects must be considerated. A related method was introduced in

[KAJI83] for the ray tracing of fractal terrains and in [HART91] for the ray tracing of objects

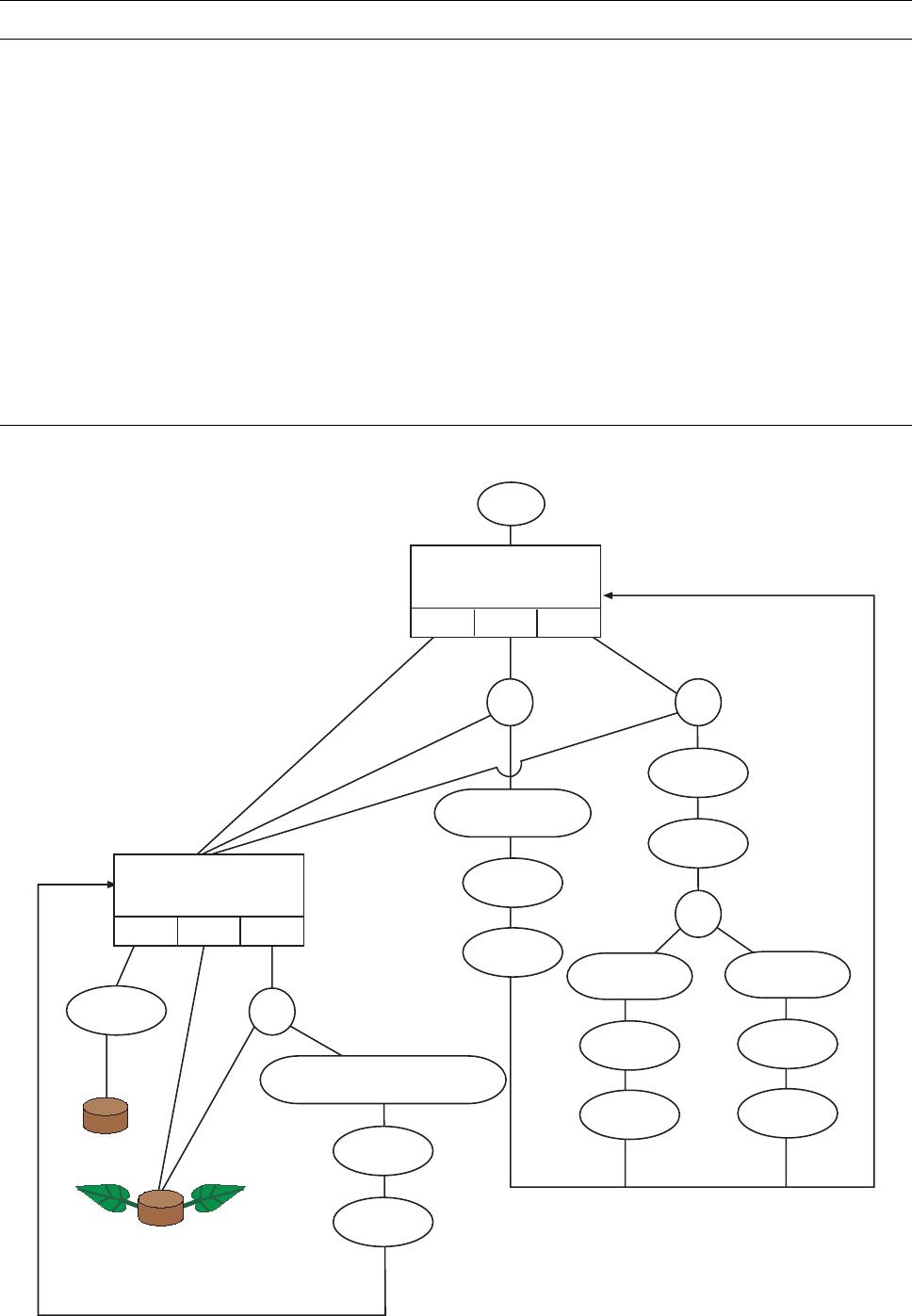
defined by Iterated Function Systems (IFS). Fig.1.1a shows a CSG-PL-System, that generates a

simple sympodial branching structure and Fig.1.1b the corresponding CSG graph. A full description

of this approach we gave in [GERV95].

Initialization of the parameters

{ cnt = 8; // order of the branching structure

trunk = 2, // number of t runk segments (cycl es of rule with index 2)

fTR = 0.96; // scaling factor for trunk segments

gamma = -72.0; // divergence angle

alpha1= -60.0; // branching angles

alpha2 = 20.0;

fBR1 = 0.73; // scaling factors for left and right branches

fBR2 = 0.67;

noleaves = 3; // if cnt is less than noleaves the limbs bear leaves

segments = 2; // number of segments for a limb with leaves

fxSG = 1/7; // scaling factors for segment cylinders

fySG = 1/7;

dSG = 1/segments; // height of a segment cylinder

fLV = 0.6; // scaling factor for leaves

} TR // the start node

of 10

免费下载

图数据库 csggraph

关注

评论